| 1. | ||
| 2. | ||
| 3. | ||
| 4. | ||
| 5. | ||
Computational Experiment for Analysis of Main Parameters of the Gas Filtration Process in Porous Medium
N. Ravshanov, N. M. Kurbonov
Laboratory of "Modeling of Complex Systems", Center for Development of Software Products and Hardware-Software Complexes, Tashkent, Uzbekistan
Email address
(N. Ravshanov) 
(N. M. Kurbonov) Citation
N. Ravshanov, N. M. Kurbonov. Computational Experiment for Analysis of Main Parameters of the Gas Filtration Process in Porous Medium. American Journal of Mathematical and Computational Sciences. Vol. 1, No. 1, 2016, pp. 29-36.
Abstract
The article provides three-dimensional nonlinear mathematical model of the process of gas filtration in a porous medium, and the results of computational experiments. During the calculation of the pressure distribution in different fields of the input data, the dependence of flow rates of the filter coefficients and viscosity, formation thickness, porosity factor, heterogeneity of filtration field and the arbitrariness of its boundaries.
Keywords
Mathematical Model, Computing Experiment, Borehole, Flow Rate, Filtration, Gas, Pressure, Viscosity
1. Introduction
Extraction of oil and gas is an important part of the real economy in the modern world. Increased production of energy is associated with the main stages of the projecting process for the development and deployment of new oil and gas fields.
In order to accelerate the process of designing and developing new oil and gas fields, improving the technical and economic indicators of reservoir oil and gas recovery systems, as well as the most complete product recovery from old oil and gas deposits, it is necessary to conduct comprehensive studies using effective methods and means.
Many scientists from different countries are involved with the solution to these problems, and to date they have produced significant results of fundamental and applied nature.
Particularly, the study [1] is devoted to the latest advances in the development of a continuous approach to the modeling of the dusty gas flow in isotropic porous structures. Over the past fifty years this approach has attracted considerable attention due to the need to develop models of the dusty gas stream that can describe different phenomena, including in relation to the subsurface transport of dissolved or suspended solids, structures of liquid-dust separators, analysis and design of filtration systems. To date developed a number of models for the gas particles flow through porous media, taking into account, as the behavior of a macroscopic flow and microscopic interactions that arise from the porous microstructure. A detailed study of porous microstructures leads to better understanding the interaction between the involved phases and the strength of the porous matrix, acting on the fluid phase. Models dusty gas flow and particle transport in porous structures are characterized by a mathematical idealization porous microstructures.
In [2], the results of numerical modeling of gas flow in a porous medium initially saturated with gas and water, accompanied by the formation of gas hydrate. It is shown that depending on the parameters of the environment at the outer edge (permeable or impermeable to gas flow) of hydrate formation may occur only once on the front edge and in the extended region.
In the work [3] tasks on the flat radial inflow gas to the well taking into account the temperature of the reservoir are presented. Difference schemes of differential equations, initial and boundary conditions corresponding to these differential equations are constructed. As a result of the decision of non-isothermal gas filtration problem in several productions of the analysis of the solutions obtained for the pressure and temperature of the formation, carried out a comparison of the calculated values of the process gas filtration characteristics (temperature and pressure) with their measured values for the gas wells of one of the deposits of Western Siberia. It was shown that after 10 hours of bottom hole pressure to substantially stabilized, and the temperature continues to decrease after 100 days of its operation. During the 100 days of work well in the bottom temperature decreases to 4°C, at the same time for the first day, it decreased by 2°C, and in the next 99 days of its decrease was 2°C.
In work [4] the method of numerical solution of equation single-phase unsteady gas filtration in a porous medium is described. Linearization of Leibenson classical equation is conducted. To solve the resulting linear equation efficient numerical algorithm without saturation in the space variables and time is built.
In work [5], the transport problem is considered in the porous medium a three-phase mixture "water-oil-gas" in the case where the water contains a finely dispersed gas phase in the form of micro- or nano-bubbles. It is assumed that the transfer of bubbles is mainly determined by the passage of the dispersed phase (water). These large aggregations of gas phase in the pore space, as well as water and oil carried in accordance with the modified Darcy law for multiphase mixtures. A mathematical model of motion of the mixture is built, when the main phases (water, gas, and oil) are subject to filtering equations and the fine gas phase is described by the Boltzmann equation type.
In work [6] a numerical model of gas filtration in porous heterogeneous environments is proposed, which is developed based on the finite element method with fractional time derivatives. We consider the fractional derivatives of Caputo and Riemann-Lowville. A numerical analysis using experimental input data were conducted.
In [7] an experimental study of the phenomenon, associated with the formation and destruction of the condensate plugs during filtration two-phase hydrocarbon mixture (methane, butane) with the help of a one-dimensional model of gas condensate reservoir. The developed mathematical model allows the calculation of hydrodynamic and thermodynamic characteristics of filtration process of hydrocarbons in the stratums. Quantitative and qualitative agreement of results of experiments and computational dependences are obtained.
For controlling the process of gas filtration, liquid hydrocarbons, oil and water in homogeneous and heterogeneous porous medium it is important to repeatedly solve systems of nonlinear or quasi-linear partial differential equations of parabolic type, determine the hydrodynamic (mathematical) objects of management model [8]. In the work for this hierarchical multigrid options of balance and variational methods in conjunction with the methods of domain decomposition, splitting into physical processes and spatial coordinates. The work consists of two parts. The first part deals with a single-phase model of gas filtration in the development of gas fields in the second - two-phase flow of oil and water - oil fields. This presentation shows the versatility of the proposed results. Due to multi-level partitioning and splitting of the original initial-boundary value problem for the equations of the model is possible to build cost-effective solutions using algorithms of multiprocessing computing systems of cluster type parallel action.
In the article [9] the process of discretization of mathematical model of distributed object - natural gas deposit is presented. As the research object the abstract gas deposit was chosen and represented as gas-bearing stratum of parallelepiped form with production wells. The lower part of the deposit filled with formation water. Accordingly the strata pressure’s alteration lies in the core of deposits geological processes, three dimensional models is necessary. Model is shown by the equations describing the change of a strata pressure in each point of deposit space, border and initial conditions, equations for gas filtration speed, equation for gas-water contact, input function and deposit gas output. The computational experiment of gas drive based on developed model with some assumptions had been conducted.
Specifically, in [10] a mathematical model that allows you to get the permeability into gas, water and condensate by displacing water, gas and condensate was created, additionally oil, gas and water at a water displacement gas and oil.
Analysis of the above mentioned sources and other scientific papers showed that in studies it is not considered taking into account the non-linearity of gas filtering patterns in porous media. In this paper, efforts have been made to fill this gap.
2. The Statement of the Problem
To solve above mentioned problems, we consider the continuity equation for the area G, not including the wells:
(1)
and in particular nodes, where the well
(2)
Where 
- volumetric flow rate (at atmospheric pressure) in the wells of tasks, 
- mass flow, 
- atmospheric pressure, 
- the density, b – power of the stratum,
(3)
Substituting equation (3) in (2) and taking into account the variability of the capacity of the reservoir will get:
(4)
where 
- the average power value in the "square", 
- respectively the filtration coefficient and viscosity of the gas,
We assume that the gas is ideal and we obtain [11-14]:
(5)
Equation (5) is valid for any law of filtration and any dependence on the density of the pressure.
If in the equation (5) all coefficients are constant, i.e., 
, we obtain the well-known equation Leybenson
(6)
To carry out numerical experiments on a computer, using the equation:
; 
; 
,
we give the dimensionless form to the equation (6):
(7)
To solve the formulated problem to the equation (7) we add initials, boundary and internal conditions:
(8)
. (9)
3. The Solution of the Problem
As the developed mathematical model of the object is described by nonlinear differential equations in partial derivatives with their respective initial, internal and boundary conditions, to obtain a solution, which is difficult in an analytical form.
One of the main methods, which allow determining patterns of change in the filtration variables, is the method of approximation of differential operator equations, which describe the finite-difference conservative scheme, effectively implemented on a computer, enabling a comprehensive study of the object and exposing it through a set of external and internal disturbances.
To solve the equations (7) - (9) we enter steady grid through x and y:
if 
.
Substituting in the problem (7) - (9) differential operators into finite-difference, using a scheme of longitudinal-transverse direction in the areas 
and 
we get [11-14]:
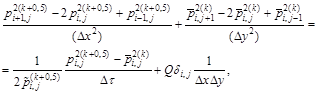(10)
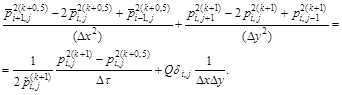(11)
We add designations:
(12)
(13)
Putting (12) into (13) and (10) into (11) and by naming 
and 
we get:
(14)
and
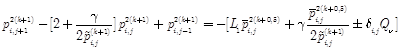(15)
Equations (14) and (15) we present in the form of a system of algebraic equations:
(16)
and
(17)
where
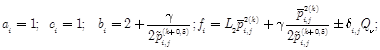
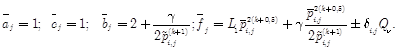
The solution of equation (16) and (17) is searched by the sweep method.
To solve nonlinear equations (16) - (17) an iterative method is used. Conditions for the convergence of the iterative process have following form:
,
where 
- the given value (
), 
- the number of iterations.
4. Discussion of Results
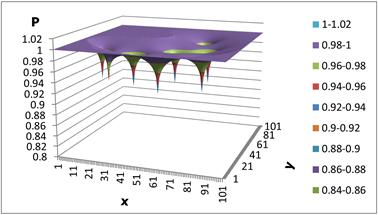
Based on the developed mathematical software package in the language of «Delphi» were compiled and a series of numerical experiments on a computer for different values of parameters and conditions of the gas in porous medium. According to the results of the numerical calculations, maps of isobars are drawn (pressure change) by years for arbitrary filtering area (Figures 1 - 6).
The analysis of numerical calculations (Figure 4) showed that with an increase in the coefficient of variation in filtration, the pressure change in filtration field is reduced significantly. This is particularly evident in the points where the wells are located in the area around them.
As it is clear from the analysis of conducted computational calculations (Figure 5) the main factor affecting the process of gas filtration in porous medium is a filtration coefficient, the coefficient of the porous medium, filtration field heterogeneity and its arbitrariness, flow rate of wells, power of the sheet, coefficient of response of oil and gas and viscosity. With the growth of the filtration coefficient, the interference area of wells to the process of significantly increases over time. Numerical calculations were performed for various well capacities when one, two, four, eight wells are acted. Numerical calculations, which were carried out in the piecewise heterogeneous filtration fields, showed that changes of wave of pressure’s perturbation in these areas are heterogeneous.
Numerical calculations have also been carried out for 8 working wells with equal capacity (Figure 6). The analysis of the computational experiments showed that while extracting the gas from the deposit the gas pressure gradually decreases in the porous medium. Since the wells are located unevenly, there is an uneven pressure drop around wells depending on the distance between them. The difference in pressures especially noticeable in the area of the seventh well.
The calculation program can also be used in the design, forecasting, refinement of design solutions of gas fields and underground gas storage facilities.
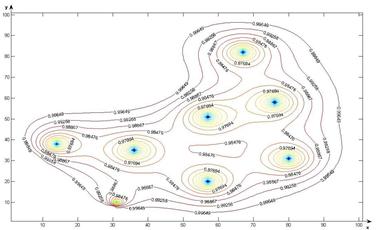
a)
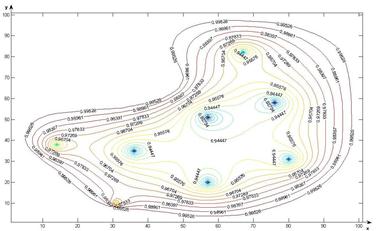
b)
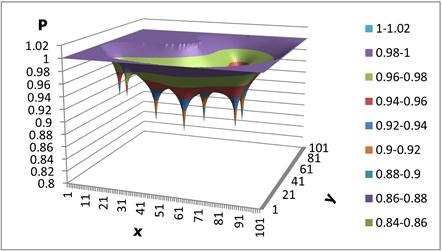
Figure 1. The gas pressure change in the field of filtration (when filtering coefficient equals to 0.4, the filtration time is 365 days).
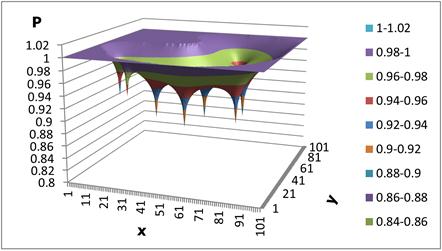
In figures 1 - 3 the results of a numerical calculation on a computer with an arbitrary field of gas filtration in layers and functioning 8 wells (at t = 365; 1825; 3650 days) are shown. As follows from the numerical calculations, the pressure around the wells is reduced gradually at a constant rate of filtration and pressure reduction is distributed in the area under consideration with the expiration time. Filtering time t = 1825 days around 8 wells formed a common area where the combined isobaric lines around the wells. Because of the numerical computer calculation shows that the change in pressure filtration depends essentially on the location of wells in the area under consideration, and their flow rates.
a)
b)
Figure 2. The gas pressure change in the field of filtration (when filtering coefficient equals to 0.4, the filtration time is 1825 days).
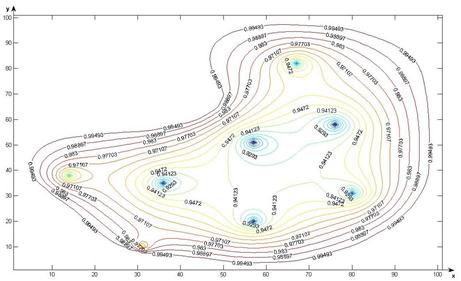
a)
b)
Figure 3. The gas pressure change in the field of filtration (when filtering coefficient equals to 0.4, the filtration time is 3650 days).
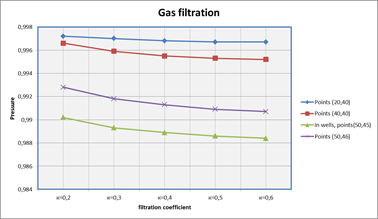
Figure 4. The gas pressure change in the filtration field, depending on the changes in the filtration coefficient.
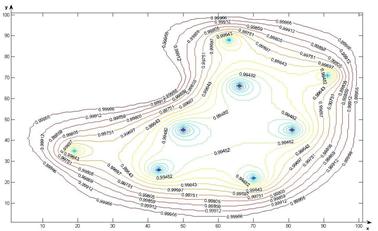
Figure 5. Gas pressure changes in heterogeneous filtration area (the filtration time equal to 1825 days).
Figure 6. The redistribution of the gas pressure in the porous medium per days.
5. Conclusion
Based on the traced computational experiment that the pressure around the holes gradually decreases at a constant filtration rate, and decrease the pressure in the considered area extends over time.
Computational experiments found that with an increase in the coefficient of filtration, the pressure change in the filtration field is reduced significantly.
The developed software of the tested process can be used for numerical calculations on a computer for analysis, forecasting, making managerial decisions for the development and projection of oil and gas fields under various conditions influencing the producing formation and the adoption of concrete and practical recommendations, depending on the hydrogeological and geophysical properties of porous medium.
References
