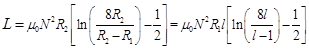The Influence of the Numerical Integration with Matlab and Mathematica Programming in the Treatment of the Logarithmic Singularity of the Inductance of the Pancake
Slobodan Babic1, *, Cevdet Akyel2, Levent Erdogan3, Bojan Babic4
1Département de Génie Physique, École Polytechnique, C. P. 6079 Succ. Centre Ville, QC H3C 3A7, Montréal, Canada
2Département de Génie Électrique, École Polytechnique, C. P. 6079 Succ. Centre Ville, QC H3C 3A7, Montréal, Canada
3Faculty of Science, University of Prince Edward Island, 550 University Avenue, Charlottetown, PE, C1A 4P3, Canada
4Independent Consultant, 36 Gabrielle Roy, H3E 1M3, Montréal, Canada
Email address
(S. Babic)

(C. Akyel)

(L. Erdogan)

(B. Babic)
*Corresponding author
Citation
Slobodan Babic, Cevdet Akyel, Levent Erdogan, Bojan Babic. The Influence of the Numerical Integration with Matlab and Mathematica Programming in the Treatment of the Logarithmic Singularity of the Inductance of the Pancake. American Journal of Mathematical and Computational Sciences. Vol. 1, No. 1, 2016, pp. 62-66.
Abstract
Even though the self-inductance calculation of the disk coil (pancake) has been given by many authors (Spielrein, Grover, Dwight, Kalantarov, Kajikawa, Babic, Akyel, Yu, Conway, Luo) it is also the challenge in this time to obtain the simpler form of presented formulas. The expressions for calculating the self-inductance of the pancake are given over the convergent series, complete elliptic integrals or generalized hypergeometric functions. Definitely the closed form doesn’t exist except in the special cases. The propose of this paper is to give relatively simple and fast method comfortable for the potential users such as physicist and engineers. With the Mathematica code all proposed different formulas give the same results for all range of the parameters describing the disk coil (pancake). All expressions are obtained over the complete elliptic integral of the first kind and two terms given by the simple integrals which converge on the whole interval of integration. These integrals only drop to infinity (logarithmic singularities) when the radiuses of the pancake are the same and it is the case of the self-inductance of the circular loop of the negligible cross section. Numerical integration proposed by Matlab and Mathematica programming can have the significant influence in the treatment of the logarithmic singularities. We gave also the approximate formulas in the case of the circular loop which cross section can be considered not negligible.
Keywords
Self-Inductance, Thin Disk Coil (Pancake), Logarithmic Singularity, Numerical Integration
1. Introduction
Several monographs and papers are devoted to the calculation of the self-inductance of the thin disk coil (pancake) with air core [1-12]. Spielrein [1] gave the calculation of the self-inductance of the pancake by using the convergent series. In the calculation of this important electrical parameter, Conway [10] used generalizes hyper-geometric functions and elliptical integrals. Luo [11] obtained the self-inductance of the pancake from the self-inductance of the thick circular coil of the rectangular cross section. He found the limit case when the thickness of the circular coils of the rectangular cross section is negligible. This limit case led to Spielrein’s formula expressed over a convergent series. Yu and Han [6] used the formula for the self-inductance of the circular coil of the rectangular cross section but in the limit case of negligible thickness they obtained the self-inductance of the pancake expressed over complicated simple integrals. It is evident from all of these methods that the closed form of the self-inductance of the pancake doesn’t exist except in some singular cases. It is interesting to find the simplest formula for calculating this important electrical quantity. In this paper, two simple formulas are compared for calculate this quantity. These formulas programed in Matlab and Mathematica to find the influence on numerical integration. The propose of this paper is to give relatively simple and fast methods adapted for the potential users such as physicists and engineers. We target the numerical integration of the presented integrals by using Matlab and Mathematica codes which give the same or satisfactory results for some range of parameters (l greater than 1) describing the geometry of the disk coil (pancake). For some range of these parameters (l very close to 1), the Matlab code gives erroneous results. With the Mathematica code, all the different formulas proposed give the same results for all ranges of the parameters describing the disk coil (pancake).
2. Basic Expressions
In [7-8], the self-inductance of the thin disk coil (pancake) was calculated (See Fig. 1) by,
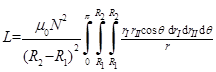 (1)
(1)
where
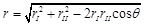
In (1), L is integrated over rI,, rII and θ respectively. The self-inductance of a disc coil is obtained as an analytical/numerical combination expressed over the complete elliptic integrals of the first kind and two members, which will be solved numerically. All kernels of these integrals are continuous functions on the intervals of integration because all singularities are smartly eliminated in the process of calculation. The self-inductance of the thin disk coil can be calculated as,
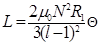 (2)
(2)
where
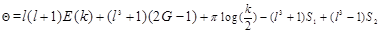 ,
,
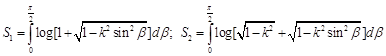
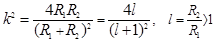 .
.
where G = 0. 9159655941772190..., Catalana's constant, [13] and E is complete elliptic integrals of the first kind, [12].
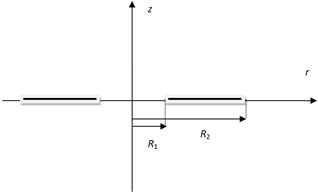
Fig. 1. Schematic drawing of a disk coil.
3. Calculation Method
The mutual inductance of the disk coil (2) was given in [8] and calculated and tested in Matlab software. For the large value of the report l, (2) gives very precise results which agree with results given in [8] and [10]. However, for values of l less than 1.000001, the formula (2) does not give consistent results using Matlab. We made some mathematical transformations in integrals S10 and S20 to extend the application of the self-inductance (2) also for the values of l = R2 ∕R1 which are close to 1.
Thus, the new form is obtained to calculate the self-inductance of the pancake,
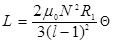 (3)
(3)
where
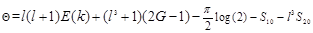 ,
,
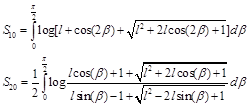 ,
,
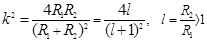 .
.
As it will be shown through examples, these transformations did not bring the expected improvement in the Matlab software by using the different Matlab codes of the numerical integrations. We can explain these results by the problems which appear because of the logarithmic singularity which occurs when l is very close to 1. The formulas (2) and (3) are programmed in the Mathematica software and both give results in the large scale of l values which perfectly agree with results obtained by approaches given in [10]. Before giving the comparative numerical analysis by different numerical integrations in Matlab and Mathematica, let us first consider all special cases.
3.1. l = 1 (R1 = R2)
This case is the well-known singular case which gives,
 (4)
(4)
3.2. R1= 0, R2= R (The Self-Inductance of a Full Disk)
Using some transformations in Θ, expression (3) can be obtained in the form where l'Hôpital's rule can be applied that leads to the self inductance of a full disk coil,
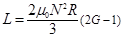 (5)
(5)
Also this formula has been obtained in [10]. G is Catalan's constant previously given in the formula (2) and in [13].
3.3. R1 → R2 (Inner Radius Tends Toward the Outer Radius)
This case leads to the well-known formula [10],
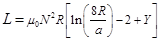 (6)
(6)
where R is the turn radius, a is the radius of the circular wire from which the turn is constructed. If the current flows only on the wire surface (due to the skin effect) Y = 0, and current flow is homogeneous in the wire then Y = 0.25.
3.4. l ≈ 1 (The Case of a Logarithmic Singularity: R1 ≈ R2)
Conway [10] gives the analogous formula,
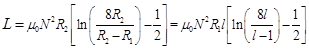 (7)
(7)
Thus, the complete set of formulas is given to calculate the self-inductance of the disk coil (pancake) by using only the complete elliptic integral of the first kind as well as two simple convergent integrals which cover the complete range of the interval of integration. Obviously in the special cases, we obtained all formulas for the self-inductance of the pancake in the closed form.
4. Numerical Validation
To verify the validity of presented expressions for any value of the rapport R2/R1, we will compare results of formulas (2) and (3) using Matlab and Mathematica. Also, these results will be compared by Conway’s and Spielrein’s approaches.
4.1. Example 1
In these calculations, we calculate the normalised self-inductance regarding the inner radius and the number of turns (L∕(N2R)). The formulas (3) and (4) are programmed using Matlab programming language with the Matlab code (gaussq.m) [14]. This code is based on the Gaussian numerical quadrature which gives very precise results even the kernel function has the possible singularities at the end of the interval of the integration. In Table 1, we give the comparative results between formulas (2) and (3) and those given by Spielrein and Conway [1] and [10]. It is clear from the Table 1 that formulas (3) and (4) give results which are in very good agreement when the shape factor l is greater than 1.001. The formula (3) gives more precise results than the formula (4) for the shape factor, l between 1.00001 and 1.000001. Both of them give erroneous results for the shape factor l less than 1.000001 because the singularity of the kernel function occur nearby l = 1.
Table 1. Comparison of Computational Accuracy for the shape factor l far and close from 1.
| l | LSpielrein [1] (μH∕m) | L Conway [10] (μH∕m) | LBabic-Akyel, (2), [8] (μH∕m) | LThis Work (3) (μH∕m) |
| 50 | 36.2822050627 | 36.2822050626845 | 36.2822050626845 | 36.282205062684494 |
| 10 | 8.5558078657 | 8.555807865723495 | 8.555807865723498 | 8.5558078657234961 |
| 3 | 4.1202478984 | 4.120247770949785 | 4.120247770949788 | 4.1202477709497867 |
| 1.5 | 3.9375565536 | 3.937556957309482 | 3.937556957309488 | 3.9375569573094811 |
| 1.1 | 5.1875898298 | 5.187589829874826 | 5.187589829874616 | 5.1875898298746534 |
| 1.01 | 7.8169836166 | 7.816983616632973 | 7.816983616591049 | 7.8169836166906856 |
| 1.001 | 10.6712873756 | 10.67128737563754 | 10.671287375441191 | 10.671287381233595 |
| 1.00001 | 16.4524421475 | 16.45244214746880 | 16.452465803942653 | 16.775648549663888 |
| 1.000001 | 19.3458776688 | 19.34587766869611 | 19.324144742411551 | 20874.833623746886 |
| 1.0000001 | 22.2393823064 | 22.23938230721058 | 26.290791221797604 | -7013430.280374610 |
Table 2. Comparison of Computational Accuracy for the shape factor l far and close from 1.
| l | LSpielrein [1] (μH∕m) | L Conway [10] (μH∕m) | LBabic-Akyel, (2), [8] (μH∕m) | LThis Work (3) (μH∕m) |
| 50 | 36.2822050627 | 36.28220506268449 | 36.28220506268449 | 36.28220506268449 |
| 10 | 8.5558078657 | 8.555807865723495 | 8.555807865723495 | 8.555807865723495 |
| 3 | 4.1202478984 | 4.120247770949785 | 4.120247770949785 | 4.120247770949786 |
| 1.5 | 3.9375565536 | 3.937556957309482 | 3.937556957309482 | 3.937556957309482 |
| 1.1 | 5.1875898298 | 5.187589829874826 | 5.187589829874826 | 5.187589829874826 |
| 1.01 | 7.8169836166 | 7.816983616632973 | 7.816983616632973 | 7.816983616632973 |
| 1.001 | 10.6712873756 | 10.67128737563754 | 10.67128737563754 | 10.67128737563754 |
| 1.00001 | 16.4524421475 | 16.45244214746880 | 16.45244214746880 | 16.45244214746880 |
| 1.000001 | 19.3458776688 | 19.34587766869611 | 19.34587766869611 | 19.34587766869611 |
| 1.0000001 | 22.2393823064 | 22.23938230721058 | 22.23938230721058 | 22.23938230721058 |
From Table 1, it is obvious that in Matlab the formula (2) is more suitable for numerical evaluation than the formula (3) in the cases where the shape factor l is very close to 1. The formula (3) gives enormous errors particularly when l is lesser than 1.0000001.
The programming of formulas (2) and (3) was made in Mathematica with the numerical integration given by default (See Table 2). From presented results obtained by formulas (2) and (3) from this work, and from Spielrein’s and Conway’s approaches, we can see that all of them are in an excellent agreement. From Table 2, we see that in Mathematica, the formulas (2) and (3) give the same results to their numerical evaluation in the cases where the shape factor l is very close to 1.
From Tables 1 and 2, the influence of the numerical integrations of formulas (2) and (3) by using the Matlab and Mathematica software is given. Thus, we confirmed that formulas (2) and (3) have to give the same results as Conway’s formula.
4.2. Example 2
In this example, the self-inductance of the disk will be calculated when l is very close to 1 until the extreme case l = 1 for which the self-inductance is ∞, (4).
From Table 3, when l is very close to 1, expressions (2) and (3) give the same results as Conway’s approach. This means that the numerical integration given in Mathematica can be used either for very small or very large values of l. This was not always the case in Matlab when the code of the numerical integration is given by default.
Table 3. Comparison of Computational Accuracy for the shape factor l close from 1.
| l-1 | L Conway [10] (μH∕m) | LThis Work (3) (μH∕m) | L (7) (μH∕m) |
| 10-1 | 5.187589829874826 | 5.187589829874826 | 4.998068846886786 |
| 10-2 | 7.816983616632973 | 7.816983616632973 | 7.784316262102376 |
| 10-3 | 10.67128737563754 | 10.67128737563754 | 10.66658208170639 |
| 10-6 | 19.34587766869611 | 19.34587766869611 | 19.34586862407991 |
| 10-8 | 25.13289502932351 | 25.13289502932351 | 25.13289490994222 |
| 10-10 | 30.91992242891705 | 30.91992242891705 | 30.91992242743389 |
| 10-12 | 36.70694995725958 | 36.70694995725958 | 36.70694995724185 |
| 10-15 | 45.38749125213918 | 45.38749125213918 | 45.38749125213915 |
| 10-16 | 48.28100501710534 | 48.28100501710534 | 48.28100501710534 |
Thus, the code of the numerical integration given in Mathematica must be considered as the most reliable code of the numerical integration.
4.3. Example 3
Calculate the self-inductance of the full disk of the radius R = 1 m and with N = 1000 turns.
This calculation is obtained in purely analytical form (5),
L = 0.6966 H
5. Conclusion
In this paper, we have demonstrated, through relatively simple expressions in the calculation of the self-inductance of a thin disk coil, that self-inductance is expressed over the complete elliptic integral of the first kind and that two simple integrals do not have an analytic solution. Although the complete solution for calculating the self-inductance of the pancake is given by J. T. Conway using generalized hyper-geometric functions which are closely related to elliptic integrals, the presented formulas are better suited for fast engineering applications and they give the same results as Conway’s formula in Mathematica software. Using Matlab, the presented formulas give the same results as in Mathematica except for the cases of nearby possible singularity where the kernel functions oscillate considerably. From presented examples using many different formulas for the calculation of the self inductance of the thin disk coil (pancake) in which we compared the influence of the numerical integration with Matlab and Mathematica programming we can conclude that with the Mathematica code all proposed different formulas give the same results for all range of the parameters describing the disk coil (pancake). Thus, for the logarithmic singularities which appear in electromagnetic problems with Mathematica programing we obtain the results of very high accuracy with very fast computational time.
References
- J. Spielrein, Arch. El. 3, (1915), pp. 187.
- F. W. Grover, 'Inductance Calculations', New York: Dover, (1964), chs.2 and 13.
- H. B. Dwight, 'Electrical Coils and Conductors', McGraw-Hill Book Company, INC. New York, (1945).
- Chester Snow, 'Formulas for Computing Capacitance and Inductance', National Bureau of Standards Circular 544, Washington DC, (1954).
- P. L. Kalantarov et al., 'Inductance Calculations', Moscow, USSR/Russia: National Power Press, 1955.
- D. Yu and K. S. Han, 'Self-Inductance of Air-Core Circular Coils with Rectangular Cross-Section', IEEE Trans. on Mag., Vol. 23, No. 6, (1987), pp. 3916-3921.
- S. Babic and C. Akyel, 'An Improvement in Calculation of the Self- and Mutual Inductance of Thin-Wall Solenoids and Disk Coils', IEEE Trans. on Magnetics, Vol. 36, No. 4, pp. 678-684,2000.
- S. I.Babic and C. Akyel, 'An Improvement intheCalculation of the Self -Inductance ofThin Disk Coilswith Air-Core,' WSEAS Transaction on Circuits and Systems 3(8), 1621-1626, 2004.
- H. A. Wheeler, 'Simple inductance formulas for radio coils', Proceedings of the IRE, Vol 16, No.10, October 1928.
- J. T. Conway, 'Analytical Solutions for the Self and Mutual Inductances of Concentric Coplanar Disk Coil', IEEE Transactions on Magnetics, Digital Object Identifier: 10.1109∕TMAG.2012.2229287, 2012.
- Y. Luo, 'Improvement of Self Inductance Calculations for Circular Coils of Rectangular cross Section', IEEE Transactions on Magnetics, Digital Object Identifier:10.1109∕TMAG.2012.2228499, 2012.
- Kazuhiro Kajikawa and Katsuyuki Kaiho, 'Usable Ranges of Some Expressions for Calculation of the Self-Inductance of a Circular Coil of Rectangular Cross Section', Cryogenic Engineering, Vol. 30, No. 7 (1995), pp. 324-332, (In Japanese).
- M. Abramowitz and I. A. Stegun, 'Handbook of Mathematical Functions', National Bureau of Standards Applied Mathematics, Washington DC, (1972), Series 55, p. 595.
- http://www.mathworks.com/matlabcentral/fileexchange/32-gaussq.

 (S. Babic)
(S. Babic)  (C. Akyel)
(C. Akyel)  (L. Erdogan)
(L. Erdogan)  (B. Babic)
(B. Babic) 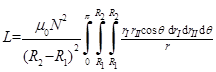
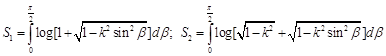

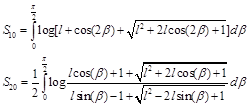 ,
,