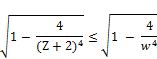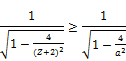Efficient Simple Tests for Primality
Fayez Fok Al Adeh
President of the Syrian Cosmological Society, Damascus, Syria
Email address
Citation
Fayez Fok Al Adeh. Efficient Simple Tests for Primality. American Journal of Mathematical and Computational Sciences. Vol. 1, No. 2, 2016, pp. 79-88.
Abstract
The tests form ageneral method to decide whether a given positive odd integer is composite or prime. The tests are based on the divisibility properties of the sum of two squared positive integers. The algorithms comprising the tests are polynomial- time algorithms.
Keywords
Algorithm, Composite, Generating Function, Greatest Common Divisor, Prime, Quotient, Remainder, Solving Polynomial Equation, Square
1. Introduction
If x is an odd positive integer, then the simplest way to discover whether it is composite or prime is to try and divide x by every number from one up to 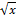 . If x is a ten – digit number, the number of necessary operations may exceed 100000, but if x is a fifty – digit number, the number of elementary steps may rise to a one followed by 25 zeros. The ultra – computer running at 1 teraflop will take in the order of one million years to complete the job on average. That does not sound terribly efficient. The problem is that the number of stepsis rising exponentially in the number of digits of the given number. Algorithms like this, that require an exponentially increasing number of steps with respect to the size of the input are regarded as intractable. They are non polynomial- time algorithms.
. If x is a ten – digit number, the number of necessary operations may exceed 100000, but if x is a fifty – digit number, the number of elementary steps may rise to a one followed by 25 zeros. The ultra – computer running at 1 teraflop will take in the order of one million years to complete the job on average. That does not sound terribly efficient. The problem is that the number of stepsis rising exponentially in the number of digits of the given number. Algorithms like this, that require an exponentially increasing number of steps with respect to the size of the input are regarded as intractable. They are non polynomial- time algorithms.
However, there is a more efficient algorithm for finding prime factors of large composites. It is based on finding another positive integer M which is relatively prime to x. M is called the seed. The key step is to calculate the order of M with respect to x. Now in the next step the seed is raised to a power equal to the order and the square root is taken. From this last result add 1 or subtract 1` to give a pair of numbers N1 and N2. In the final step, the greatest common divisor of x and N1 and also of x and N2 are calculated. The pair of greatest common divisors thus obtained are factors of x. Because the seed number is chosen randomly, there is no guarantee for the success of the method. The problem with this algorithm, is that, for conventional computer, finding the order of large numbers also requires a large number of steps which would grow exponentiolly. Peter Shor’s great insight was to discover that finding the order of a number is an easy job in quantum computing. But to use Shor’s algorithm on a large scale, we have to wait until quantum computing is introduced in the empirical applications.
2. Test - 1
Given an odd positive integer x >1, we have to dicide whether x in prime or composite.
TEST – 1 – employs any updated algorithm for calculating the square root of a number. Since the algorithm gives approximate value of the square root, we can check for the two odd integral values less and greater than the approximate one. If the square root of x is an integer, then x is composite, and we are done. Else, we move to TEST-2-.
3. Test – 2
Consult an updated table of primes. Let the largest known prime in the table be Z. We divide x successively by the primes in the table. The division operations will not take too much time on a moderate computer.
If one of the primes divides x, then x is composite, and we are done.
Else, we move to TEST-3-.
4. Towards Test – 3
We proceed to formulate TEST -3 – by proving the following theorem.
Theorem -1- Given two positive integers x and y (x > y, x, y >1). If (xy+1) divides (x2+y2), then the quotient must be a square.
First of all, we prove the following lemma.
Lemma 1-1 If x and y are relatively prime positive integers (x > y, x, y>1), then (xy+1) does not divide (x2+y2).
Proof: Suppose that (xy+1) divides (x2+y2) i.e.
(xy+1)│((x2+y2) (1)
The notation m│n refers here to the fact that the integer m divides the integer n.
we know that
(xy+1)│(x2 y2-1) (2)
from (1) we deduce that
(xy+1) │(x2 y2+y4) (3)
using (2) and (3) we arrive at the result
(xy+1)│(y4+ 1) (4)
i.e. there exists a positive integer r such that
r (xy+1) = y4+1 (5)
taking residues mod y we deduce that
r ≡ 1mod y (6)
this means that there exists a positive integer w such that
r = wy+1 (7)
using (7) we rewrite (5) in the form
(xy+1) (wy+1) = y4+ 1 (8)
it is evident from (8) that w cannot be greater than y or equal to y, in fact
w<y (9)
from (8) we get the following equality:
xwy + x+w = y3 (10)
according to (10), if w and y have a common divisor, then this divisor must also divide x. This contradicts our assumption that x and y are relatively prime. Hence w and y are relatively prime.
equation (8) tells us that
(wy+1)│(y4+1) (11)
also we know that
(wy+1)│(w2y2-1) (12)
from (11) and (12) we arrive at the result
(wy+1)│y2(w2+y2) (13)
since (wy+1) and y2 have no common prime divisor, we deduce that
(wy+1)│(w2+y2) (14)
We began with two positive relatively prime integers: x, y (x>y) satisfying the divisibility condition (1) and ended with two positive relatively prime integers: the original y, and a new positive integer w (w<y) satisfying the divisibility condition (14).
Beginning with (14) and repeating similar steps, we arrive at two positive relatively prime integers: the original w, and a new positive integer s (s<w) satisfying a similar divisibility condition:
(sw+1)│(s2+w2) (15)
We cannot go on repeating similar steps, because of the principle of the impossibility of infinite descent. This proves the lemma.
Proof of Theorem -1-
the assumed divisibility condition is
(xy+1)│(x2+y2) (16)
according to (16), lemma 1-1 implies the existence of agreatest common divisor w of x and y: i.e.
x = aw (17)
y = bw (18)
a>b (since x >y) (19)
so, the rational fraction
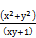 (20)
(20)
must be an integer, we have
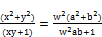 (21)
(21)
a and b are relatively prime positive integers.
here we have two cases: either
(w2ab + 1) │(a2+ b2) i.e. (22)
(a2+ b2)> (w2ab + 1) or
(w2ab + 1) = (a2+ b2) (23)
assume (22), we know that
(w2ab + 1) │(w4a2b2- 1) (24)
from (22) we deduce that
(w2ab + 1) │ w4b2(a2+ b2)=(w4a2b2+ w4b4) (25)
Using (24) and (25) we get
(w2ab + 1)│(w4b4+1) i.e. (26)
r(w2ab + 1) = (w4b4+1) (27)
where r is a positive integer.
taking the residues mod w2b
r≡ 1mod w2b (28)
i.e. there exists a positive integer m such that
r=mw2 b + 1 (29)
thus (27) takes the form
(w2ab + 1)(mw2 b + 1) = (w4b4+1) (30)
assumethat
m ≥ b hence (31)
(mw2 b + 1) ≥ (w2b2+1) (32)
we have also, since a>b
(w2ab+1)>(w2b2+1) (33)
from (32) and (33) we get
(w2ab + 1)(mw2 b + 1)>(w2b2+1)2> (w4b4+1) (34)
this contradiction leads us to the result that
m< b (35)
expanding (30) we get
mw4ab2+ w2ab+ mw2b+1= w4b4+1 i.e.
mw2ab+a+m = w2b3 (36)
suppose that there exists a prime number which divides both b and m, then according to (36), this prime number must divide a, contrary to the fact that a and b are relatively prime. Therefore b and m are also relatively prime.
(30) tells us that
(mw2 b + 1)│(w4b4+1) but (37)
(mw2 b + 1)│(m2w4b2-1) (38)
from (37) and (38) we deduce that
(mw2 b + 1)│(m2w4b2+w4b4)= w4b2(m2+b2) (39)
it is evident that (mw2 b + 1) and w4b2 have no prime factor in common, therefore
(mw2 b + 1)│(m2+b2) (40)
We began with two positive relatively prime integers: a, b (a>b) satisfying the divisibility condition (22) and ended with two positive relatively prime integers: the original b, and a new positive integer m (m<b) satisfying the divisibility condition (40).
Beginning with (40) and repeating similar steps, we arrive at two positive relatively prime integers: the original m, and a new positive integer s (s<m) satisfying a similar divisibility condition:
(w2sm+1)│(m2+ s2) (41)
We cannot go on repeating similar steps, because of the principle of the impossibility of infinite descent. Therefore, our assumption (22) is false and we are left with the result (23) that
w2ab+1=a2+ b2 (23)
(21) and (23) prove Theorem -1-
We return to our main problem: given an odd positive integer x>1, to decide whether x is composite or prime. If there exists a positive integer y (y<x) such that the divisibility condition (1) is satisfied, then according to Theorem -1-:
(x2+y2) = w2(xy+1) (42)
where w is the greatest common divisor of x and y.
Here we have three cases:
Case -1-
y2> w2>x (43)
from (42) we get
x2+y2= w2(xy+1)>x(xy+1) i.e.
x2+y2> x2y+x hence (44)
x(x-1) > y(x2–y) (45)
sincey2> xwe get
x(x-1) > y (x2-y) >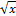 (x2-y) i.e.
(x2-y) i.e.
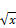 (x-1) > (x2–y) but x>
(x-1) > (x2–y) but x>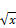 , therefore (46)
, therefore (46)
x (x-1) >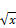 (x-1) > (x2-y) hence (47)
(x-1) > (x2-y) hence (47)
x2-x > x2-y i.e.
- x>-y, x<y (48)
this contradicts our main assumption that y<x.
Therefore, Case -1- does not occur.
5. Test - 3
We deal here with
Case -2-
w2≤y2<x (49)
from (42)
y2=x(w2y-x)+w2 (50)
if w2y-x > 0 then
y2>x (51)
contrary to our assumption (49)
if w2y-x<0 then x (w2y-x)<0and hence
x (w2y-x) + w2<w2 i.e. y2< w2
contrary to our assumption (49)
therefore
w2y-x = 0 (52)
in this case (50) tells us that y2=w2 i.e.
y=w (53)
substituting in (42) we get x2 + w2 = w3x+w2 i.e.
x=w3 (54)
TEST -3- can employ any simple algorithm to check if x is a cube of an integer. Since the algorithm gives approximate value of the cubic root, we can check for the two odd integral values less and greater than the approximate one. If x is a cube of an integer, then the divisibility condition (42) is satisfied and x is (afortiori) composite.
In case TEST -3- fails, we move on to TEST-4-
6. Towards Test – 4
We proceed to formulate TEST - 4 - by considering:
Case - 3 –
y2>x>w2 (55)
according to Theorem -1-(x2+y2) = w2(xy+1) i.e.
x2 =(w2x –y) y+w2 if (56)
w2 x=y then x2=w2 i.e. (57)
x=w (58)
contrary to our assumption (55)
if w2x-y<0 then (w2x-y) y<0 and hence
x2= (w2x-y) y+w2<w2 i. e.
x<w (59)
this contradicts (55), so we are left with the result that
w2x-y>0 (60)
we can prove in this case that an infinite sequence of values of x and y satisfy the divisibility condition of Theorem -1-, let
x1 =w2x-y, y1 =x (61)
we have that
x12+ y12= (w4x2+y2-2w2xy) +x2
= (x2+y2)+ w2x(w2x-2y)
= w2(xy+1)+w2x(w2x-2y)
= w2xy+w2+w4x2-2w2xy
= w4x2-w2xy+w2
= w2(w2x2-xy+1)
=w2[x(w2x-y)+1]
= w2(x1y1+1) (62)
according to (53),(54) and (61) the first elements of the sequence would be:(where yn+1 =xn)
Table 1. According to (53), (54) and (61) the first elements of the sequence would be:(where yn+1 =xn).
| n=0 | x0=o | y0=-w |
| n=1 | x1=w | y1=0 |
| n=2 | x2=w3 | y2=w |
| n=3 | x3=w5-w | y3=w3 |
| n=4 | x4=w7-2w3 | y4=w5-w |
| n=5 | x5=w9-3w5+w | y5=w7-2w3 |
note that lines n=0 and n=1 correspond to Case -1-, while line n=2 corresponds to Case -2-. This sequence of numbers, satisfies according to (61) the recurrence:
xn+2 = w2xn+1 –xn given that (63)
x0=0, x1=w, x2=w3 (64)
we will solve for the generating function
A(z)=A=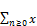 nzn (65)
nzn (65)
multiply (64) by zn and sum over all values of n
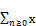 n+2zn=w2
n+2zn=w2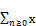 n+1zn-
n+1zn-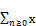 nzn i.e.
nzn i.e.
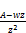 =
=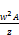 – A (66)
– A (66)
from which we get
A=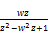 (67)
(67)
rewrite (67) in the form
A= 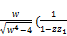 -
- 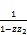 ) (68)
) (68)
where z1 =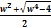
z2 =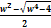 therefore
therefore
A = 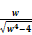 (
(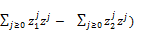 (69)
(69)
now xn is the coefficient of the nth power of z, i.e.
xn=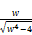 [
[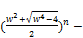 (
(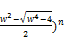 ] (70)
] (70)
this is the required general formula.
Let us prove that, if n is a multiple of 3, then the corresponding element of the sequence would be even, and hence must be discarded, since it cannot be equated to the given positive odd integer x. Since w divides the given positive odd integer x, it must be odd. Suppose that for some value of n which is a multiple of 3 (n=3m), the corresponding element xn of the sequence is even, while yn is odd. According to (63), xn would be odd and yn even for n=3m+1. Now, for n=3m+2, and using (63) again, we conclude that both xn and yn are odd. Employing (63) for n=3m+3 leads us to the conclusion that the element xn of the sequence is even, while yn is odd. In reference to Table-1 we see that for n=3, the element x3 of the sequence is even, while y3 is odd (because w is odd). By mathematical induction, our claim is justified. The first elements of the sequence given in Table-1 can be easily deduced from (70).
If the given positive odd integer x equals an element of the sequence xn for some value of n, then x must be composite.
Assume that for some n, it is the case that:
x= 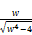 [(
[(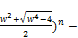 (
(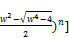 (71)
(71)
where x is the given positive odd integer, we make the substitution
t =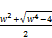 hence (72)
hence (72)
w= 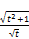 (72) takes the form (73)
(72) takes the form (73)
x = 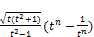 (74)
(74)
if we expand this equation in powers of t, we get
t4n+2+ t4n-x2 t2n+3-2t2n+2+2x2 t2n+1-2t2n-x2t2n-1+t2+1=0 (75)
in reference to (71), where it is evident that w divides x, assume that w ≤ Z (Z the largest known prime mentioned in TEST -2). w cannot be prime, since this would contradict the negative result of TEST -2. If w is composite, then some prime p less than or equal to Z divides w, and hence divides x. Again this would contradict the negative result of TEST -2. Therefore w> Z, i.e. w≥ Z+2.
We make use of the following very well known theorem;
A theorem for the upper limit to the real roots:
If, in a real equation
f(z) =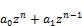 +…..+
+…..+ 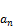 (
(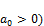
the first negative coefficient is preceded by k coefficients which are positive or zero, and if G denotes the greatest of the numerical values of the negative coefficients, then each real root is less than 1+ 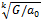
in case of equation (75) we have
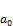 =1, G=x2, k=2n-1 (76)
=1, G=x2, k=2n-1 (76)
therefore, the upper limit to the real roots t in this case is
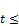 1+
1+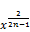 (77)
(77)
according to (72)
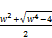 =
= 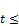 1+
1+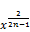 (78)
(78)
since Z+2≤ w (Z the largest known prime mentioned in TEST – 2 –(, we have
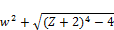 ≤
≤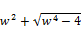 ≤ 2(1+
≤ 2(1+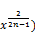
i.e.
w≤ [2(1+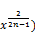 -
- 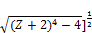 (79)
(79)
according to (71), the given positive odd integer x would be equal to an element of the sequence xn, i.e.
x= 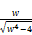 [(
[(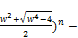 (
(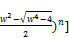 (80)
(80)
hence we have
x = 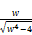 (
(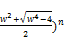 [1-(
[1-(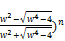 ]
]
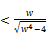 (
(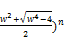
=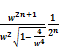 (1+
(1+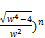
<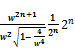
= 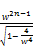 (81)
(81)
since Z+2 ≤ w we have
(Z+2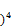 ≤
≤ 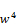
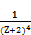 ≥
≥ 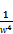
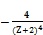 ≤
≤ 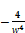
1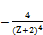 ≤1
≤1 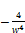
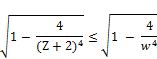
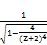 ≥
≥ 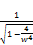 (82)
(82)
from (82)
x<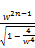 ≤
≤ 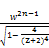 (83)
(83)
therefore
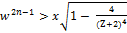 i. e.
i. e.
w>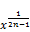 (
(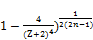 (84)
(84)
if, for a given n, we assume that x =xn, we get a polynomial equation in the unknown w. In this case (79) and (84) represent the upper and lower bounds of the unknown w, respectively.
rewrite equation (71) in the form
x=w [(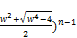 +(
+(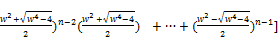 (85)
(85)
according to (85), and since x is given, we note that if w increases, n decreases, and vice versa.
If we assume that t is known, and ofcourse x is known, then we can determine the value of n as follows, rewrite (74) in the form
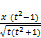 =
= 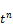 -
- 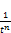 (86)
(86)
making the following substitutions:
d=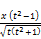 v =
v = 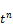 (87)
(87)
transforms (86) into a quadratic equation
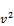 -dv -1=0 (88)
-dv -1=0 (88)
taking the positive root of (88)
v = 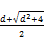 (89)
(89)
and substituting tn for v according to (87), we can calculate the value of the unknown n assuming that t is known.
To get an upper bound for n, according to what we have already mentioned, we substitute (Z+2) for w in (72) and go on to solve equation (88) and get the positive root v. Using this root we get a value for n from (87). From this value, we calculate the least positive integer not divisible by 3 greater than or equal to the value. Let this integer be n2.
Let r be the greatest odd positive integer less than or equal to 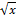 . To get a lower bound for n, according to what we have already mentioned, we substitute r for w in (72) and go on to solve equation (88) and get the positive root v. Using this root we get a value for n from (87). From this value, we calculate the greatest positive integer not divisible by 3 less than or equal to the value. Let this integer be n1.
. To get a lower bound for n, according to what we have already mentioned, we substitute r for w in (72) and go on to solve equation (88) and get the positive root v. Using this root we get a value for n from (87). From this value, we calculate the greatest positive integer not divisible by 3 less than or equal to the value. Let this integer be n1.
We are ready now for TEST – 4 –
7. Test - 4
We formulate TEST -4 – as an algorithm applicable on any moderate computer.
1. for i=n2 to n1 step -1.
2. if i is divisible by 3, then goto 18.
3. Substitute i for n in (84) and get the lower bound r1 of the unknown w. let w1 be the greatest positive odd integer less than or equal to r1.
4. Substitute i for n in (79) and get the upper bound r2 of the unknown w. let w2 be the least positive odd integer greater than or equal to r2.
5. if i ≠ n2, then goto 10.
6. for j= w1 to w2 step 2.
7. if j divides x, then goto 20.
8. next j.
9. goto 16
10. for j =w1 to v1 step2.
11. if jdivides x, then goto20.
12. next j.
13. for j =v2 to w2 step2.
14. if j divides x, then goto 20.
15. next j.
16. v1= w1-2.
17. v2= w2+2.
18. next i.
19. print: TEST -4- has already failed, goto the section entitled: TOWARDS TEST -5-.
20. halt, print: x is composite and we are done.
8. Towards Test - 5
Now it is the case that although the divisibility condition of Theorem -1- does not hold, yet x may be composite.
So, we assume that for a positive integer y (y<x), we have:
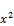 +
+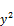 = a (xy+1)+b (90)
= a (xy+1)+b (90)
wherea is the quotient, and b the remainder.
here we have three cases:
Case -1-
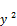 >a+b>a>x (91)
>a+b>a>x (91)
therefore
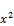 +
+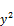 = a (xy+1)+b
= a (xy+1)+b
= a xy+a+b
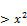 y+a+b
y+a+b
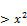 y+x i.e.
y+x i.e.
x(x-1) > y(x2-y) (92)
from (92)
x(x-1)> y (x2-y) >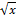 (x2-y) i.e.
(x2-y) i.e.
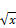 (x-1)> (x2-y) (93)
(x-1)> (x2-y) (93)
but x >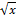 hence
hence
x(x-1) > (x2-y)
x2-x> x2-y
-x>-y
x<y (94)
this contradicts our main assumption that y<x, therefore Case -1- does not occur.
Case -2-
a <a+b ≤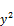 < x (95)
< x (95)
from (91)
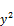 =x(ay-x) + a+b (96)
=x(ay-x) + a+b (96)
if ay-x >0 i.e. ay>x then
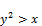 (97)
(97)
this contradicts (95)
if ay-x < 0 then from (96)
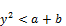 (98)
(98)
again this contradicts (95)
therefore
ay-x=0 x=ay (99)
we give in Table-2 the first elements of a sequence, this corresponds to x2 and y2 in the line n=2 of that sequence.
we write (99) in the form
y= 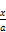 =w (100)
=w (100)
we use the letter w here, because the divisibility condition (42) is a special case of the non – divisibility (90), where w2 corresponds to a, and b equals zero. In the special case, (100) takes the form y2 =w= 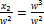 .
.
Case -3-
y2>x>a+b>a (101)
from (90)
x2 = y(ax-y) +a+b if (102)
ax-y=0 then ax=y (103)
which means that x<y, in contradiction to our original assumption x>y.
if ax-y<0, then from (103)
x2<a+b (104)
since y2<x2 we have
y2<x2<a+b (105)
this contradicts (102). therefore
ax-y>0 (106)
we can prove in this case that an infinite sequence of values of x and y satisfy (91).
let
x1= ax-y y1=x (107)
we have that
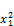 +
+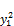 =(ax –y
=(ax –y 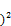
= a2x2+y2-2axy+x2
= x2+y2+a2x2-2axy
=a(xy+1)+b+a2x2-2axy
=a+b-axy+a2x2
=ax(ax-y)+a+b
= ay1x1+a+b
=a(x1y1+1)+b (108)
thus there is a recurrence of the form
xn+2=a xn+1- xn (109)
which generates the sequence xn.
according to (90), (100), (107), and (109), the first elements of the sequence would be (where yn+1=xn)
Table 2. According to (90),(100),(107), and (109), the first elements of the sequence would be (where yn+1=xn).
| n=0 | x0=0 | y0 = -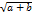 |
| n=1 | x1=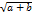 | y1 = 0 |
| n=2 | x2=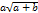 | y2 = 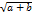 |
| n=3 | x3=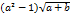 | y3 =a 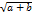 |
| n=4 | x4=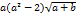 | y4 =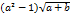 |
note that lines n=0 and n=1 correspond to case -1- (y2>a+b>a>x) which does not occur, while line n=2 corresponds to case -2- (a<a+b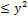 <x).
<x).
we will solve for the generating function
A(z)=A=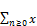 nzn (110)
nzn (110)
multiply (110) by zn and sum over all values of n
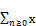 n+2zn=a
n+2zn=a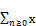 n+1zn-
n+1zn-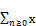 nzn i.e. (111)
nzn i.e. (111)
hence
A –x0-x1z= az(A-x0) –Az2 (112)
Az2-azA+A=x0+x1z-azx0
=x0+z(x1-ax0) (113)
A=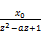 +
+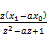 (114)
(114)
using Table-2 we get
A=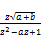 (115)
(115)
following the same steps as with equation (67), we abtain the result
xn=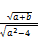 [(
[(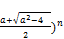 - (
- (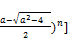 (116)
(116)
the first elements of the sequence given in Table-2 can be easily deduced form (116). We mentioned that the divisibility condition (42) is a special case of the non- divisibility (90), where w2 corresponds to a, and b equals zero. In reference to (109), we see that all the elements of the sequence (116) are integers, hence (a+b) must be a square. According to what we have already mentioned, we write (a+b)=w2. Therefore (116) transforms to
xn=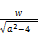 [(
[(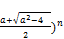 - (
- (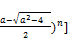 (117)
(117)
And the first elements of the sequence in Table-2 become
Table 3. And the first elements of the sequence in Table-2 become.
| n=0 | x0=0 | y0 = -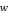 |
| n=1 | x1=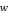 | y1 = 0 |
| n=2 | x2=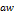 | y2 = 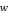 |
| n=3 | x3=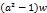 | y3 =a 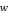 |
| n=4 | x4=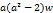 | y4 =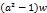 |
note that every element of the sequence is divisible by w. Whenever we equate the given positive odd integer x with any element of the sequence, we deduce that w must be odd. We can also prove that a must be odd. To this end, we suppose that a is even (and hence b odd, sincew2 =a+b). Rewrite (90) in the form
x2 +y2= a(xy+1)+b=axy+a+b=axy+w2 (118)
assume that y is odd, and take the remainders mod 4
1+1 0(or2)+1 mod 4 (119)
0(or2)+1 mod 4 (119)
In both cases of the remainders o (or 2), equation (119) is impossible, hence y must be even. We conclude that if a is even, then y is even for all values of n in the sequence. In fact if a is even, the elements of the sequence alternate between odd and even values as we can easily prove. (for both sequences of x and y)
If x2n is even and y2n is odd using the recurrence (109) we deduce that x2n+1 is odd and y2n+1 is even and x2n+2 is even and y2n+2 is odd. Since x2 is even and y2 is odd, our claim is justified. We conclude therefore that a must be odd and b even. Returning to (118) and taking the remainders mod 2, we get:
1+y2 y+1 mod 2 i.e. 2
y+1 mod 2 i.e. 2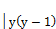 (120)
(120)
and y may be odd or even, which is the case.
Whenever we equate the given positive odd integer x with an element of the sequence, then since w divides such an element, we deduce at once that w must be greater than Z, i.e. w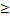 Z+2 (Z is the largest known prime in TEST-2-). This is because, if w
Z+2 (Z is the largest known prime in TEST-2-). This is because, if w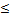 Z, then w would be equal to a prime p
Z, then w would be equal to a prime p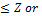 divisible be a prime p
divisible be a prime p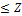 which means that x would be divisible by the same prime, contradicting the result of TEST-2-
which means that x would be divisible by the same prime, contradicting the result of TEST-2-
assume that
a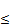 Z (121)
Z (121)
since x and y are both divisible by primes greater than Z, we deduce that a is relatively prime to both x and y The condition of non – divisibility (91) applies, we can follow similar steps and get:
x2+a2=a1(xa+1)+b1= a1xa+a1+b1=a1xa+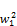 (122)
(122)
y2+a2=a2(ya+1)+b2=a2ya+a2+b2=a2ya+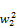 (123)
(123)
It is evident from (122) that if w1 and a have a common divisor, this common divisor would divide x, contradicting our result that x and a are relatively prime. Moreover, if w1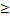 x, then from (122)
x, then from (122)
x2+a2=a1xa+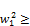 a1xa+x2 i.e. a
a1xa+x2 i.e. a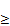 a1x (124)
a1x (124)
contradicting the fact that x>a, hence
w1<x (125)
also it is evident from (123) that if w2 and a have a common divisor, this common divisor would divide y, contradicting our result that y and a are relatively prime. Moreover, if w2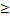 y, then from (123)
y, then from (123)
y2+a2=a2ya+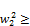 a2ya+y2 i.e. a
a2ya+y2 i.e. a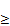 a2y (126)
a2y (126)
contradicting the fact that the value of each element yn of the y sequence begining with n=3 onwards is greater than a, hence
w2<y (127)
adding (122) and (123) we get
x2+y2+2a2=a(a1x+a2y)+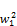 +
+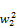 (128)
(128)
taking the remainders mod a
x2+y2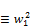 +
+ 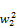 mod a (129)
mod a (129)
taking the remainders mod a for equation (118) we get
x2+y2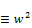 mod a (130)
mod a (130)
from (129) and (130) we arrive at the result
w2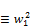 +
+ 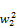 mod a (131)
mod a (131)
we began with two positive integers x, y satisfying the non-divisibility condition (90) and hence (130) and ended with two positive integers w1<x and w2<y satisfying (131), since w1 and aare relatively prime, and w2 and a are also relatively prime, we can formulate two new equations:
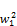 +a2=a3w1a+
+a2=a3w1a+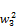 (132)
(132)
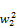 +a2=a4w2a+
+a2=a4w2a+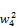 (133)
(133)
and conclude that
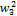 +
+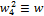 2 mod a
2 mod a
(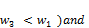 (
(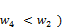 (134)
(134)
we cannot go on repeating similar steps, because of the principle of the impossibility of infinite descent, thus our assumption that a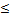 Z is false and
Z is false and
a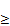 Z+2 (135)
Z+2 (135)
Let us equate the given odd positive integer x with an element of the sequence
x=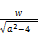 [(
[(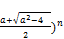 - (
- (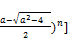 (136)
(136)
we make the substitution
t = 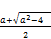 hence (139) takes the form (137)
hence (139) takes the form (137)
x=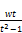 (tn-
(tn-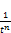 ) (138)
) (138)
we expand this equation in powers of t
wt2n-xtn+1+xtn-1- w =0 (139)
refering to the theorem for the upper limit to the real roots of a polynomial equation, we have for equation (142)
a0=w, G=x, K=n-1 (140)
therefore, the upper limit to the real roots t in this
case is
t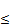 1+(
1+(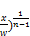 (141)
(141)
but  < x
< x
and since w<x, we have
t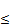 1+(x
1+(x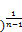 (142)
(142)
according to (140)
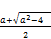 = t
= t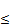 1+(x
1+(x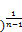 (143)
(143)
since Z+2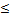 a (Z the largest known prime mentioned in TEST-2-) we have
a (Z the largest known prime mentioned in TEST-2-) we have
a +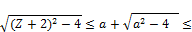 2 (1+x
2 (1+x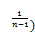
i.e.
a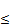 2 (1+x
2 (1+x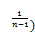 -
- 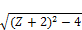 (144)
(144)
from (136)
x=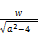 (
(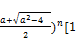 - (
- (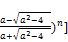
<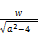 (
(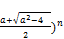
= 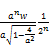 (1+
(1+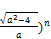
<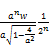 2n
2n
= 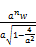
Since Z+2 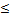 a
a
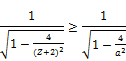
Since w =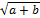 <
<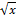 wehave x<
wehave x<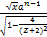
i.e. 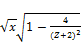 < an-1 hence (145)
< an-1 hence (145)
a>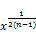 (1-
(1-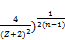 (146)
(146)
If for a given n, we assume that x=xn, we get a polynomial equation in the unknown a. In this case (144) and (146) represent the upper and lower bounds of the unknown a, respectively.
As in the case of divisibility, we have to prove that, if n is a multiple of 3, then its’ corresponding element of the sequence xn is even, and hence must be discarded.
Suppose that for some value of n which is a multiple of 3 (n=3m) the corresponding element xn of the sequence is even, while yn is odd. According to (109), xn would be odd and yn even for n=3m+1. Now for n=3m+2, and using (109) again, we conclude that both xn and yn are odd. Employing (109) for n=3m+3 leads us to the conclusion that the element of the sequence
xn is even, while yn is odd. In reference to Table-3 we see that
for n=3 the element x3 is even, while y3 is odd. By mathematical induction, our claim is justified.
Rewrite (136) in the form
x=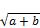 [(
[(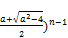 +(
+(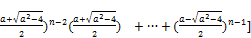
According to this equation, it is evident that, since x is given, if a increases, n decreases, and vice versa.
Rewrite (138) in the form
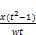 =tn-
=tn-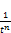 (147)
(147)
making the following substitutions
d=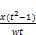 v= tn (148)
v= tn (148)
transforms (147) into a quadratic equation
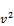 -dv -1=0 (149)
-dv -1=0 (149)
taking the positive root of (149)
v = 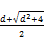 (150)
(150)
and substituting tn for v according to (148)
we can calculate the value of the unknown n. Here we assume that t and w are known, and ofcourse x is known.
To get an upper bound for n, according to what we have already mentioned, we substitute (Z+2) for a in (137) and also for w in (147) and go on to solve equation (149) and get the positive root v from (150). Using this root, we get a value for n from (148). From this value, we calculate the least positive integer not divisible by 3 greater than or equal to the value. Let this integer be m2. Let n2 be the greatest of m2 and the previous n2 of TEST-4. Ofcourse, if they are equal, we take any one of them.
We know from (100) that x>a+b (=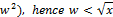 . Reviewing the elements of the Table-2 we arrive at the result that for all values of n
. Reviewing the elements of the Table-2 we arrive at the result that for all values of n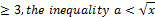 is satisfied.
is satisfied.
Let r be the greatest odd positive integer less than or equal to 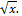 To get a lower bound for n, we substitute r for a in (137) and for w in (147) and go on to solve equation (149) and get the positive root v from (150). Using this root we get a value for n from (148). From this value, we calculate the greatest positive integer not divisible by 3 less than or equal to the value.
To get a lower bound for n, we substitute r for a in (137) and for w in (147) and go on to solve equation (149) and get the positive root v from (150). Using this root we get a value for n from (148). From this value, we calculate the greatest positive integer not divisible by 3 less than or equal to the value.
Let this integer be m1. Let n1 be the smallest of m1 and the previous n1 of TEST-4-. Ofcourse, if they are equal we take any one of them.
since 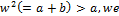 deduce that
deduce that 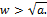
using (146) we arrive at the result
w>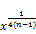 (1-
(1-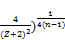 (151)
(151)
This is a lower bound for w.
we get from equation (136)
x=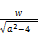 (
(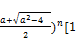 - (
- (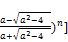 we have that (152)
we have that (152)
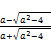 =
=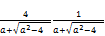 <
<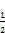 hence (153)
hence (153)
(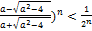 therefore
therefore
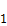 - (
- (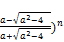 >1-
>1-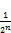 (154)
(154)
from (144) we can calculate an upper bound for 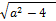 . Let this upper bound be U1, hence
. Let this upper bound be U1, hence
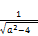 >
>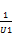 (155)
(155)
from (146) we can calculate a lower bound for
(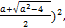 let this lower bound be U2.
let this lower bound be U2.
We deduce from (152) by using (154) that
x>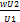 (
(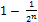 ) i.e.
) i.e.
w<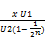 this is an upper bound for w. (156)
this is an upper bound for w. (156)
now we are ready for TEST-5
9. Test - 5
1. for i=n2 to n1 step -1.
2. if i is divisible by 3, then goto 15.
3. substitute i for n in (84) and get the old lower bound r2 of the unknown w, let w2 be the greatest positive odd integer less than or equal to r2.
4. substitute i for n in (151) and get the new lower bound r1 of the unknown w, let w1 be the greatest positive odd integer less than or equal to r1
5. if r2< r1 then goto 9.
6. for j= r1 to r2 step 2.
7. if j divides x then goto 17.
8. next j.
9. substitute i for n in (79) and get the old upper bound r1 of the unknown w, let w1 be the least positive odd integer greater than or equal to r1.
10. substitute i for n in (153) and get the new upper bound r2 of the unknown w, let w2 be the least positive odd integer greater than or equal to r2.
11. If w1> w2 then goto 15.
12. for j= w1 to w2 step 2.
13. If j divides x then goto 17
14. next j
15. next i
16. print: x is prime: halt: we are done.
17. print: x is composite: halt: we are done
References
- Aigner, Martin; Ziegler, Gunter M. (2002) "Proofs from The Book", New York; Springer – Verlag.
- Ribenboim, Paulo (1988) "The Book of Prime Number Records", New York; Sprintger.
- Wilf, Herbert S. (1994) "Generatingfunctionology", London; Academic Press.
- Dickson, Leonard Eugene (1922) "First Course in The Theory of Equations", New York; John Wiley.
- Schroeder, M.R.(1986) "Number Theory in Science and Communication", New York; Springer – Verlag.
- Rader, Robert J.(1978) "Advanced Software Design Techniques", Princeton; Petrocelli Books,Inc.
- Koblitz,Neal (1987) "A Course in Number Theory and Cryptography", New York; Springer – Verlag.
- Guy, Richard K.(1994) "Unsolved Problems in Number Theory", New York; Springer – Verlag.
- Govindarajan, Sathish; Maheshwan, Anil, Editors, (2016) "Alogorithms and Discrete Applied Mathematics", New York; Springer – Verlag.
- Moreno,Carlos J.; Wagstaff, Samuel S. Jr.(2005), "Sums of Squares of Integers", CRC Press.