| 1. | ||
| 2. | ||
| 3. | ||
| 4. | ||
| 5. | ||
Application of Immune Algorithm for Constructing a Model of Fuzzy Inference
Mukhamediyeva D. T.*, Niyozmatova N. A.
Centre for the Development of Software and Hardwarily-Program Complex of Tashkent University of Information Technologies, Tashkent, Uzbekistan
Email address
(Mukhamediyeva D. T.) 
(Niyozmatova N. A.) Citation
Mukhamediyeva D. T., Niyozmatova N. A. Application of Immune Algorithm for Constructing a Model of Fuzzy Inference. American Journal of Mathematical and Computational Sciences. Vol. 1, No. 2, 2016, pp. 74-78.
Abstract
The main characteristics of fuzzy immune algorithms and build a model of fuzzy inference based on the use of immune algorithms are discussed in the paper. The proposed algorithm is built on the basis of the synthesis of normal immune evolutionary approach to the ideas of adaptive optimization. Using this approach the problem of creating a model of fuzzy inference based on the use of immune algorithm is solved and software product is created.
Keywords
Fuzzy Sets, Immune Algorithm, Optimization, Model, Logical Inference, Synthesis, Adaptation
1. Introduction
Recently, immune algorithms are becoming a powerful computing means in a variety of optimization tasks.
As known, the natural immune system is a complex system comprised of several functionally different components. The immune system uses a multi-layered defense against foreign antigens, including the effect of non-specific (innate) and specific (acquired) protective mechanisms. The primary role of the immune system is the recognition of all cells (or molecules) of the body, and classifying them as "our" or "alien". Alien cells undergo further classification in order to stimulate the defense mechanism of the appropriate type. In the evolution of the immune system learns to distinguish between alien antigens (such as bacteria and viruses) and its own cells and molecules of the body.
It is found that a large number of immune cells in the body is maintained, that circulate throughout the body. The main type of cells involved in the immune response and having the properties of specificity, diversity, memory and adaptability are lymphocytes. Other cells that have the names of phagocytes - neutrophils, eosinophils, basophils, and monocytes - helper cells, whose main function is to ensure the ability of the immune system to destroy the antigen. In the body there are two main types of lymphocytes - B and T lymphocytes.
These two types of lymphocytes play a different role in the immune response, although it may interact, by controlling in this way their functions.
When the antigen enters the body, only a small part of the cells of the immune system is able to recognize it. Such detection processes stimulates reproduction and differentiation of lymphocytes, resulting in the formation of clones of identical cells (or antibodies). This process, called multiplication clone population generates numerous specific antigen antibody-producing cells. Reproduction of clone immune cells leads to the destruction or neutralization antigen. Part of the resulting cells is retained for immunological memory. As a result, the following effect for similar antigen leads to more rapid immune response (secondary response).
The process of circulation of B and T lymphocytes in primary and secondary lymphoid organs is carefully controlled to provide the corresponding ingress cell populations - naive ("untrained") and effector cells and memory cells – to different destinations. Selective migration of lymphocytes in various organs and tissues is called homing (homing). In these organs there has a dedicated maintenance medium for reproduction processes of activated antigen of lymphocytes and their differentiation into effector cells and memory cells. It is interesting, that the memory cells have a selective preference for the type of tissue in which they first encountered antigen. This probably provides a return of each particular memory cell in the area of the body where it is likely to meet again with the antigen.
In practice, the development of intelligent systems has a tendency to use hybrid models for a variety of practical problems. So, with regard to the learning of fuzzy models, some authors, along with traditional methods of optimization, are using immune algorithm [5]. Experimental studies conducted by the authors, show that the use of this approach allows to achieve the best results to improve the speed and accuracy of tasks. Thus, with regard to the problem of forming the knowledge bases of expert systems it is an urgent task to develop an effective learning algorithm of fuzzy model based on intelligent methods and effective heuristic algorithms [7].
2. Computational Aspects of the Immune System
The immune system has a great interest as a system that can efficiently handle large volumes of data. In particular, it performs a large amount of complex highly parallel distributed computing. The behavior of the immune system as a whole is determined by the totality of local interactions.
The immune system functions as a "second brain" because it is able to store information about the intensity of previous contacts of its constituent cells and respond to new, not previously encountered, structures (antigens). Description of the development of immune response patterns is an interesting problem of dynamical system theory. With respect to the possible applications for information processing the following properties of immune system is perspective:
Ÿ Recognition. The immune system can recognize and classify the different molecular structures and selectively respond to them. Detection occurs during intercellular contacts, while the strength of coupling is determined by the shape of the molecules and the magnitude of electrostatic charge. Recognition of it and others is one of the main tasks to be solved by the immune system.
Ÿ Selection features. Antigen - presenting cells (APC) interpret antigenic environment and distinguish particular qualities by processing antigens and presenting antigenic peptides on their surface. Each APC serves as a "filter", repressing the molecular noise, and as a "magnifying glass", focusing the attention of lymphocyte receptors.
Ÿ Variety. The immune system uses a combinatorial mechanism (genetically-mediated process) to form a plurality of different lymphocyte receptor in order to ensure that at least one of the lymphocyte population can all interact with an arbitrary fixed (known or unknown) antigen.
Ÿ Learning. The immune system evaluates the structure of a particular antigen, using his accidental contact with components of the cell system. Learning is to change the concentration of lymphocytes, which occurs during the primary response (from the first contact with the antigen). Consequently, the immune system's ability to learn lies mainly in the mechanism of replenishment of clones, leading to the formation of new immune cells, taking into account the current state of the system (this process is named as reproducing a clone).
Ÿ The memory. A small portion of the lymphocytes, which are in activated state, becomes a memory cell (associative memory). It is believed that the lifetime of the memory cell is a dynamic variable and is determined by stimulation frequency of antigens. Using the short-term and long-term mechanisms of immune memory, immune system maintains a perfect balance between resource savings and execution functions expense of preserving the minimum necessary, but sufficient memory of previous exposure to the antigen.
Ÿ Distributed search. At its core, the immune system - a distributed system. Cells of the immune system, mainly lymphocytes, are continuously recycled through the blood, lymph, lymphoid organs and other tissues. When they meet with an antigen specific immune response is carried out.
Ÿ Self-regulation. The immune protection has the property of self-regulation. Central Authority, which controls the immune system, does not exist. Depending on the mode of entry into the body, and other properties of the antigen, regulation of the immune response may be both local and systemic.
Ÿ The threshold mechanism. The immune response and proliferation of immunocompetent cells occur only after overcoming a threshold dependent on the strength of chemical bonds.
Ÿ Joint stimulation. Activation of B lymphocytes is tightly regulated by an additional stimulus signal. The second signal (helper T lymphocytes) helps to ensure tolerance and to distinguish between serious threat and "false bell" (i.e, hazardous and non-hazardous antigens).
Ÿ Dynamic protection. Clonal reproduction and somatic hypermutation allow the immune system to produce high-affinity immune cells (a process called affinity increase), which creates a dynamic balance between studies and the protective function of the adaptive immune system. The presence of the dynamic protection gradually leads to expansion of the surveillance zone, controlled by the immune system.
Ÿ Probabilistic detection. Cross-reaction during the immune response is a stochastic process. Moreover, antigen detection always occurs inevitably in an approximate manner; hence lymphocyte may interact with several structurally similar antigens.
3. Formulation of the Problem
Let a fuzzy sample of experimental data 
, 
is given; where 
- is the n-dimensional input vector and 
- corresponding output vector.
In general, it is needed to build a model based on fuzzy inference rules:
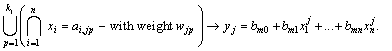
In the process of constructing the model to find the following values of the coefficients of the rules
in which the minimum of the following expression:
, (1)
where 
- the result of fuzzy rules of inference with parameters of В in the i-th sampling line.
The input matrix 
corresponds to the following fuzzy inference result:
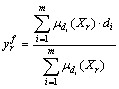; (2)
where 
- output 
-rules; 
- membership function corresponding to each of the experimental data:
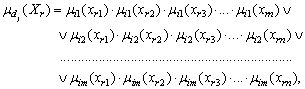
Membership functions of element 
to the term 
is as follows:
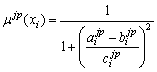
where 
- parameters of the membership functions.
The general scheme of the method is iterative and consists of the following stages.
To solve the problem (1) is used immune algorithm.
4. Setting Fuzzy Knowledge Bases Using Immune Optimization Algorithms
Immune algorithms (IA) of optimization include the following statements: cloning, mutation, aging, and selection. Let us examine them in detail.
Algorithm parameter settings and membership functions 
and 
and the weight of the rules 
consists of the following steps.
A Formation of the initial population of cloning operator generates a new generation of copies of antibodies in future populations. The following main cloning operators are known: a) static statement of cloning which simply copies each B-cell by producing transient population; b) the proportional operator of cloning that copies B-cell in proportion to their antigenic similarity; c) the probability operator of cloning, whereby the B-cells are selected from the current generation based on the likelihood of clonal selection.
For implementation of IA should specify a method of coding of fuzzy models. Let us combine the unknown parameters W, B, C into one vector:
where N- the total number of rows in the fuzzy knowledge base;
li – number of term-evaluations of the input variable 
, 
q- the total number of terms.
B Mutation operator operates depending on the existing population of clones for each antibody using a certain number of single mutations carried out randomly.
Each element of the vector S can undergo mutation operation with a probability of 
. Let us denote the mutation of element s through 
:
where 
- lower (upper) limit of the range of possible values of the weights of the rules, 
;
- the range of possible values of the stretching concentration factor of membership functions of term evaluations of the input variable , 
;
denotes the operation of finding a random number uniformly distributed on the interval 
.
C The aging operator removes the old individuals. Static aging operator uses the age parameter to the maximum number of generations of antibodies that are allowed to remain in the population. When the antibody is older, it is removed from the system, even if it may be possible to use in subsequent iterations.
At the clonal expansion a cloned antibody inherits its parent's age. After a mutation step only those antibodies that have graduated importance affinity receive age of 0. Elite option of the operator is obtained by taking the best population of antibodies to generation with age of 0.
Elite version of the statement is obtained by taking the desired antibody from a population of the generation.
D Selection operator replaces the worst antibodies in a population with new random antibodies.
On the basis of IA a software has been developed in the environment of DELPHI-7 for solving practical problems of multicriteria optimization and the results for the optimization problem from [10] are obtained.
For carrying out a comparative analysis of taken-known model problems arranged by e-mail: http://www.ics.uci.edu/~mlearn/databases/. These include the following tasks: the task of iris (Iris Data Set), glass identification task (Glass Identification Data Set), the problem of diabetes diagnosis (Pima Indians Diabetes), the environmental problem (Ecoli Data Set), task Haberman (Haberman's Survival Data Set), the task of determining the type of wine (wine Data Set), the task of determining the state of the liver (liver).
The following Table 1 shows the parameters of these tasks.
Table 1. The parameters of the model tasks.
| Name of task | Number of classes | Number of features | Number of object |
| Glass | 7 | 9 | 214 |
| Haberman | 2 | 4 | 306 |
| Iris | 3 | 4 | 150 |
| Ecoli | 8 | 7 | 336 |
| Wine | 3 | 13 | 178 |
| Liver | 2 | 6 | 345 |
In Table 2 presents the results for comparisons of the solution of some model problems on the basis of a variety of known and proposed algorithms.
Table 2. The results of the proposed and existing algorithms.
| Task | The proposed algorithm | GBC | SGF | SVM | 1NN | KNN | Conventional RBF network |
| Glass | 87.85 | 84.27 | 75.74 | 71.50 | 72.01 | 72.01 | 69.16 |
| Iris | 98.3 | 98.00 | 97.33 | 97.33 | 96.00 | 95.33 | 95.33 |
| Wine | 98.88 | 100 | 99.44 | 99.44 | 95.52 | 96.07 | 98.89 |
The following table shows the best results of the considered algorithms. The most the best results for a specific task allocated separately.
In addition, Table 3 compares the different results of our proposed algorithm, the GBC algorithms (Gravitation Based Classification) and SVM (Support Vector Machines).
Table 3. The results of the proposed and existing algorithms.
| The proposed method | GBC | SVM | |||||||
| Very bad | Very good | Bad | Very bad | Very good | Bad | Very bad | Very good | Bad | |
| Haberman | 82.7 | 87.5 | 85.1 | 75.2 | 86.7 | 81.5 | 72.3 | 82.1 | 78.8 |
| Liver | 78.4 | 86 | 82.3 | 63.5 | 72.8 | 67.1 | 60.4 | 68.3 | 65.5 |
| Ecoli | 88.5 | 94.2 | 91.8 | 89.7 | 98.5 | 95.5 | 89.4 | 94.4 | 92.3 |
5. Conclusion
Thus, we have showed the importance of combining fuzzy inference method and immune algorithms for solution of the problems with parameters containing ambiguity of various types, as well as in problems that are characterized by intuitive decisions. The proposed method can significantly improve the quality of the solution of multi-criteria optimization problems with fuzzy set parameters and criteria. For the future we are planning to study the different hybrid techniques for optimization problems, as well as automatic generation of fuzzy rule base methods. This will significantly improve the efficiency of solving optimization problems of this class.
References
