| 1. | ||
| 2. | ||
| 3. | ||
| 4. | ||
| 5. | ||
| 6. | ||
Two Theorems on Lower Defect Groups
Lijiang Zeng
Research Centre of Zunyi Normal College, Zunyi, China
Email address
Citation
Lijiang Zeng. Two Theorems on Lower Defect Groups. American Journal of Computation, Communication and Control. Vol. 3, No. 2, 2016, pp. 10-14.
Abstract
In mathematics, in applied science, even in the natural sciences, group theory has irreplaceable important position. In this article, we introduce derivation process of lower defect groups of group theory through large number of data, at first, some notations about rings, groups, characters of group first, and the using these notations prove some properties of them. Finally we give out the definitions of lower defect group, and prove two interesting theorems about lower defect groups.
Keywords
Conjugate Class, Lower Defect Group, Primitive Idempotent, Brauer Homomorphism
1. Introduction
The research of group has experienced a long process [1-6], group theory in mathematics, in applied science, even in the natural sciences has irreplaceable important position [7-9], for example, the study of quantum mechanics cannot leave the group theory, the study of molecular theory cannot leave the group theory, the study of algebraic coding cannot leave the group theory, in various fields, the role of the group theory was very great. Lower defect groups in the group theory research, has experienced a difficult process [10-11], from the derivation of lower defect groups, we can find a lot of valuable things, these things will be in various scientific research plays an important role.
This paper mainly introduces derivation process of lower defect groups, in fact, research process can be thought of as lower defect groups, perhaps, these are not new research, however, from the process, can get lot of useful research tools.
2. Some Preparation
Let G is a group, R is a ring, B1, B2,…… are all the blocks of R[G], {
} is a complete set of representatives of the conjugate classes in G consisting of p-elements, k is the number of conjugate classes in G. If T is a ring of algebraic numbers in field K and S is a subset of G, define
(1)
(2)
T will denote an arbitrary subring of K. Instead of 
we will write 
to emphasize the dependence on G. We will also write 
=
. Greg denotes the set of all p
-elements in G. Furthermore e1, e2 …are all the centrally primitive idempotent in R[G]. For each t, Bt is the block corresponding to et and k(Bt) denotes the number of irreducible characters in Bt. For a subset S of G, 
and 
is the image of 
in 
.
Observe that 
and 
. Furthermore 
is an ideal of 
which is a local ring and ideal of 
is an ideal of 
which is a local ring.
3. Some Lemmas
Lemma 1 With each block Bt it is possible to associate k(Bt) conjugate classes 
such that the following conditions are satisfied.
(i) Every conjugate class of G is associated with exactly one block.
(ii) 
is an 
-basis of 
.
Proof Let {
} be all the conjugate classes of G. let {
} be an -basis of . Then 
.
Let 
and let A denote the matrix 
, where (t, j) is the row index and i is the column index. Since A is nonsingular it is possible to arrange the classes {} so that
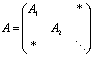(3)
Where At, is a nonsingular k(Bt)×k(Bt) matrix and the columns of At are indexed by (t,j) for each t. The result follows since 
.
Lemma 2 (Osima). Let P, Q be p-groups contained in H. Then 
, where A ranges over all p-groups in H such that 
and 
. Furthermore 
is an ideal of Z(G:H).
The proof of this lemma can be found in Reference[12].
Lemma 3 Let D be a p-subgroup of G and let 
. If C is a conjugate class of G with defect group D then 
is a conjugate class of N with defect group D. Conversely if L is a conjugate class of N with defect group D then 
for some conjugate class C of G with defect group D. ▋
The proof of this lemma can be found in Reference[13].
Let B(G) be a complete system of representatives of the conjugate classes of p-groups in G. For P
B(G) let VP (G) be the linear subspace of which is spanned by all 
, where P is a defect group of Cj. For PB(G) let
(4)
Define U(P:G)=
and V(P:G)=VP(G)
U(P:G). Let Vt(P:G)=
V(P:G)
. By lemma 2 V(P:G) is an ideal of . Therefore Vt(P:G)
=Vt(P:G)et. And if Ut(P:G)=U(P:G)
Vt(P:G), Then
V(P:G)=Vt(P:G) (5)
V(P:G)/U(P:G)
Vt(P:G)/Ut(P:G) (6)
Lemma 4 Let PB(G), let B=Bt and let {
} be defined as in lemma 1. Let 
,…,
be the subset of {} consisting of those classes which have P as a defect group. Then the image of 
in Vt(P:G)/Ut(P:G) is an -basis of this space. The number mB(P)=mB(P:G) depends only on G, B and the conjugate class of P.
Proof It is clear that
(7)
is a basis of Vt(P:G) for all t and P by (6) thus
(8)
is a basis of Vt(P:G) /Ut(P:G). The last statement is an immediate consequence.
Definition 1: If mB(P)≠0 then P is a lower defect group of B. It is said to occur with multiplicity mB(P).
Lemma 5 Let PB(G) and let B=Bt. Then mB(P:G)=
, where 
ranges over all the blocks of NG (P) with
.
Proof Let N=NG(P) and let 
be the Brauer homomorphism with respect to (G, P, N). Let 
be the primitive idempotent of Z
(G) corresponding to B and let 
, where 
ranges over all the primitive idempotents in Z(N) such that 
B for corresponding to 
. By lemma 3 is an -
isomorphism form VP(G) onto VP(N). Thus by lemma 4 induces an -
isomorphism from Vt(P:G)/Ut(P:G) onto V(P:N)
/U(P:N). By (6)
V(P:N)/U(P:N)V(P:N)/U(P:N) (9)
where ranges over all the primitive idempotents in Z(N) that occur in the sum . Therefore mB(P:G)=Dim(Vt(P:G)/Ut(P:G))=
((P:N)/U(P:N))=
(P:N).
Let S be a p-section of G. For 
define 
by
(10)
We have
Lemma 6 Let S be a p-section in G. Let B be a block of G and let e be the centrally primitive idempotent of R[G] corresponding to B. If 
then 
.
The proof of this lemma can be found in Reference [14].
Let B0(G) be a complete set of representatives of the conjugate classes of p-elements in G. If yB0(G) let S(y) denote the p-section which contains y. Let W(y:G) =W(y) be the subspace of Z(G) which is spanned by all 
with Cj
S(y). Then Z(G)=
W(y), where y runs over B0(G). By lemma 6 W(y)
W(y) for all y and t. Thus if Wt(y)=W(y)Z(G) then Wt(y)=W(y) and W(y)=
Wt(y). Furthermore Z(G)=
Wt(y). It is easily seen that if {} is defined as in lemma 1 then an R-basis of Wt(y) is formed by the set of all those 
with 
S(y). Thus the number of such classes depends only on G, B and the conjugate class of y. Define Wt,y(P:G)=Vt(P:G)W(y). And Tt,y(P:G)=Ut(P:G)W(y). Then
Vt (P:G)=
Wt,y(P:G) (11)
Vt (P:G)/Ut(P:G)
Wt,y(P:G)/Tt,y(P:G) (12)
Lemma 7 Let B=Bt, Let PB(G) and let yB0(G). let {C
} be defined as in lemma 1 and let
,…,
be the subset of {C} consisting of those classes which have P as a defect group and are contained in S(y). Then the image of 
in Wt,y(P:G)/Tt,y(P:G) is an -basis of this space. The number 
(P)=(P:G) depends only on G, B. the conjugate class of y and the conjugate class of P.
Proof The first statement follows from lemma 4 and (12). The last statement is an immediate consequence of the first.
Definition 2 If (P)≠0 then P is a lower defect group of B associated to the section S(y) which has multiplicity (P).
Lemma 8 (i)
for all PB(G); (ii)
.
Proof Immediate from the definitions.
Lemma 9 Let y be a p-element in Z(G). Then m
(P)=m
(P) for all blocks B and PB(G).
Proof The map which sends a to ay defines an -isomorphism on Z (G). It clearly preserves the ideal Vt(P:G) for all t, P and sends W(1) onto W(y). Thus it sends Wt,1(P:G)/Tt,1(P:G) onto Wt,y(P:G)/Tt,y(P:G) and the result follows from lemma 7.
4. The First Primary Outcome
Theorem 1 Let yB0(G), PB(G). Then 
, where Q ranges over the elements in B(CG(y)) which are conjugate to P in G and ranges over all the blocks of CG(y) with 
=B.
Proof Let C be a conjugate class of G with defect group P contained in S(y). Let S0 be the p-section of CG(y) containing y. Then C0=CS0 is easily seen to be a conjugate class of CG(y) which has a defect group Q that is conjugate to P in G. Conversely every such conjugate class C0 of CG(y) is of the form CS0 for suitable C. Let be the Brauer homomorphism with respect to (G, <y>, CG(y)). If C is a conjugate class of G in S(y) with defect group P then the definition of implies that 
, where 
is a union of conjugate classes of CG(y), none of which is in S0.
Let B=Bt and let e be the primitive idempotent of ZR(G) corresponding to B. Let 
, where each 
is a primitive idempotent of ZR(CG(G)). By the previous paragraph induces an –isomorphism from W(y:G)VP(G) onto 
(y:CG(y))VQ(CG(y)), where Q ranges over all elements of B(G) which are conjugate to P in G. Thus by (12) and lemma 7 induces an -isomorphism from Wt,y(P:G)/Tt,y(P:G) onto 
(Q:CG(y)). The result now follows from lemma 9.
If y≠1, then theorem 1 implies that (P) can be computed in terms of information about local subgroups of G. We will now prove some results which yield some information about 
(P).
Lemma 10 Let P be a finitely generated projective A module and let V be a finitely generated R-free A module. Then HomA(P, V) is an R-free R module and Hom
. If furthermore rankR{HomA(P, V)}=d then 
d
IK(PK, VK).
The proof of this lemma can be found in Reference [15].
Lemma 11 Let V, W be R[G] modules. Then InvG(HomR(V, W))=HomR[G](V, W).
The proof of this lemma can be found in Reference [16].
Lemma 12 Let V be a finitely generated R-free R[G] module and let W be an R[G] module. Then 
.
The proof of this lemma can also be found in Reference[16].
Lemma 13 Let U be a projective R[G] module and let 
be the character afforded by U. If y is a p-singular element then 
. If x is a p-element and Q is a Sp-group of 
then 
is an algebraic integer.
Lemma 14 Let V be a K[G] module and let 
be the character afforded by V. Then 
.
Lemma 15 
.
The proofs from lemma 13 to lemma15 all can be found in Reference [14] and [15].
Lemma 16 
.
Proof: Let V0 be the R-free R[G] module of rank one with 
. Since 
is a projective module there exists a projective R[G] module U with 
. Let be the character afforded by U. Then 
if x is a p-element, and by lemma 13 
if x is p-singular. Hence by lemma 14
Then lemma 10, lemma 11 and lemma 12 imply that 
.
Lemma 17 Let 
. Then
(13)
Furthermore 
.
Proof: 
by lemma 16. Thus lemma 15 implies the result.
Lemma 18 DetC is a power of p.
The proof of this lemma can be found in Reference [16].
Lemma 19 For each i there exists an R-linear combination 
of irreducible characters of G such that 
for 
and 
≢0(
).
The proof of this lemma can also be found in Reference [16].
Lemma 20 The elementary divisors of D are all 1. Det
is a rational integer and det
≢0(). If 
is the defect of the class containing 
then {
} is the set of elementary divisors of C.
Proof: By lemma 17 det is a rational integer. By lemma 18 the elementary divisors of D are all powers of p. Thus if the result is false, then 
has an elementary divisor divisible by 
in R. Thus there exists a set of elements {
} in R with 
for all s and 
≢0() for some i. Hence for every R-linear combination of the irreducible characters of G. This contradicts lemma 19. The last statement now follows directly from lemma 17 and lemma 18.
Lemma 21 Let V be an indecomposable R[G] module with vertex A. Let x be a p-element in G and let Q be a Sp-group of . Then 
in the ring of algebraic integers in R. In particular if p can not divisible 
then 
.
The proof of this lemma can be found in Reference [17].
Lemma 22 Let 
. Then 
if and only if 
.
The proof of this lemma can be found in Reference [13].
Lemma 23 Let B be a block of R[G] and let e be the centrally primitive idempotent in R[G] corresponding to B. Then 
.
The proof of this lemma can be found in Reference [12].
Lemma 24 Let D be a p-subgroup of G and let N=NG(D). If C is a conjugate class of G with defect group D then CCG(D) is a conjugate class of N with defect group D. Conversely if L is a conjugate class of N with defect group D then L=CCG(D) for some conjugate class C of G with defect group D. ▋
The proof of this lemma can be found in Reference [13]. Now let’s prove the second theorem of our article.
5. Another Primary Outcome
Theorem 2 Let S=S(1) be the section of G consisting of p-elements. For aR[G] let Tr(a)=
ax. Let 
be defined as in lemma 7 and for each t, P, j choose 
. Then for
B=Bt,
is an R-basis of ZR(G:S)et and
(14)
is an R-basis of Tr(R[S])et. Furthermore ChR(G:Greg, Bt)/ChR,proj(G:Greg, Bt)
ZR(G:S)et/Tr(R[S])et
as R modules.
Proof For 
ChR(G:Greg, Bt) define 
ZR(G:S). Then the map sending 
to 
is R-linear. By lemma 20 it is onto ZR(G:S). By lemma 21 ChR,proj(G:Greg)
Tr(R[S]). For a conjugate class C let D(C) be a defect group of C. If 
C then Tr(x)=|CG(x)|
. Thus {D(C)| CS} is a basis of the R module Tr(R[S]). Therefore ZR(G:S)/Tr(R[S]) is a torsion R module whose invariants are {|D(C)|| CS}. By lemma 22 this is the set of elementary divisors of the Cartan matrix of G and so ChR,proj(G:Greg)=Tr(R[s]).
By lemma 23 
. Hence ChR(G:Greg,Bt)=ZR(G:S)et and ChR, proj
(G:Greg, Bt)=Tr(R[S])et. This establishes the required isomorphism.
It follows from lemma 7 and the fact that R is a local ring that ZR(G:S)et has the required basis. Let Tt be the R module with basis
{|CG (
)|
P
B(G), 
} (15)
where B=Bt. Then TtTr(R[S])et. Clearly { |D()| 
PB(G), } is the set of invariants of the R module ZR (G: S)et/Tt. Hence ZR(G:S)et/Tt
≈ ZR(G:S)/Tr(R[S])≈ZR(G:S)et/Tr (R[S])et and so Tt = Tr (R[S])et for each t.
6. Conclusions
From the derivation process of lower defect groups in the above, we can see that the production of lower defect groups, and many of the properties associated with it, for example, we know the conjugate classes, p-elements, ring of algebraic numbers, primitive idempotent, irreducible characters such as concept, they are all in applied science and even if natural science, and important research tool.
References
Biography
