| 1. | ||
| 2. | ||
| 3. | ||
| 3.1. | ||
| 3.2. | ||
| 3.3. | ||
| 4. | ||
| 5. | ||
Improvement of Q-Learning Algorithm Convergence with Intelligent Tutoring Systems and Tabu Search
Éverton de Oliveira Paiva1, Marcus Vinicius Carvalho Guelpeli2
1Management of Educational Institutions - GIED, Federal University of Jequitinhonha and Mucuri Valleys – UFVJM, Diamantina, Brazil
2Department of Computing – DECOM, Federal University of Jequitinhonha and Mucuri Valleys – UFVJM, Diamantina, Brazil
Email address
 (E. O. Paiva)
(E. O. Paiva)  (M. V. C. Guelpeli)
(M. V. C. Guelpeli) Citation
Éverton de Oliveira Paiva, Marcus Vinicius Carvalho Guelpeli. Improvement of Q-Learning Algorithm Convergence with Intelligent Tutoring Systems and Tabu Search. International Journal of Modern Education Research. Vol. 3, No. 1, 2016, pp. 1-5.
Abstract
Using computer systems as a complement or replacement for the classroom experience is an increasingly common practice in education, and Intelligent Tutoring Systems (ITS) are one of these alternatives. Therefore, it is crucial to develop ITS that are capable of both teaching and learning relevant information about the student through artificial intelligence techniques. This learning process occurs by means of direct, and generally slow, interaction between the ITS and the student. This article presents the insertion of meta-heuristic Tabu search with the purpose of accelerating learning. Computer simulations were conducted in order to compare the performance of traditional randomized search methods with the meta-heuristic Tabu search. Results obtained from these simulations strongly indicate that the introduction of meta-heuristics in exploration policy improves the performance of the learning algorithm in STI.
Keywords
Intelligent Tutoring System, Autonomous Model, Q-Learning, Convergence Improvement, Tabu Search
1. Introduction
An Intelligent Tutoring System (FREEDMAN, 2000) [1] (ITS) is a broad term that includes any program displaying intelligence which can be employed as a learning tool. The ITS evolved from Computer-Assisted Instruction (CAI) and differs from its predecessor by the addition of knowledge learning strategies and because it keeps an updated model of the learner’s activities.
Traditional E-learning systems (LI; ZHOU, 2015) [2] were criticized for its limitations, since they always presented the same material and topics for students, regardless of their previous knowledge, level of comprehension of the subject, or learning ability. Conversely, ITS uses a database that contains knowledge expertise on the subject, learning strategies and heuristics and should be able to dynamically select relevant teaching material and thus choose different pedagogical pathways, examples and exercises for different students. Intelligent Tutoring Systems offer flexibility in the way the material is presented and greater ability to attend to students’ needs. In addition to teaching, they seek to learn relevant information about the student, thus creating an individualized learning process. ITS have been presented as highly efficient for improving student performance and motivation (PALOMINO, 2013) [3]. In order for students to acquire this ability, Artificial Intelligence (AI) techniques, such as Reinforcement Learning (RL), are used.
Reinforcement Learning (SUTTON; BARTO, 1998) [4] is a form of AI that allows a computer agent to learn from the interaction with the environment where it is found. This optimal (or almost optimal) learning method for a determined environment stems from the use of observed rewards (NORVING; RUSSELL, 2013) [5]. It is an attractive technique for solving a variety of problems when there are no available models, a priori, since its algorithms converge towards a situation of guaranteed balance (LITTMAN; SZEPESVARI, 1996) [6] and, moreover, allow for learning adequate control strategies. In this case, learning occurs by means of direct interaction between the agent and the environment. Unfortunately, the convergence of RL can only be achieved after extensive exploration of state and action spaces, which is generally slow.
However, the convergence speed of a RL algorithm can be increased be employing a few techniques. This article describes the insertion of Tabu Search as an exploration strategy of the Q-Learning algorithm with the aim of reaching a faster speed.
This article is organized into sections. Section 2 presents correlated research on ITS with autonomous model and Tabu search to speed up Q-Learning algorithm convergence. Section 3 includes the simulation methodology, ITS with autonomous model characteristics, the definition of how Tabu search works, and its adaptation to increasing the speed of Q-Learning algorithm convergence. Section 4 presents the comparative results between the original algorithm and the proposed modifications with the inclusion of Tabu search as an exploration strategy. Finally, Section 5 discusses final considerations.
2. Correlated Research
Guelpeli, Omar and Ribeiro (2004) [7] propose changes in the classic architecture of ITS by adding a new diagnostic model. This model applies RL techniques by Q-Learning algorithm (WATKINS, 1989) [8], which produces an autonomous model of the learner. A utility value is calculated based on a state-action table upon which the algorithm estimates future rewards that represent the learner’s cognitive states. The best action policy to be used by the tutor at any cognitive state is then made available by the RL algorithm, without the need for an explicit model of the learner.
Li and Zhou (2015) [2] present the architecture of an automatic knowledge acquisition (AKA) system which is able to improve teaching efficiency, since this system is capable of conducting an analysis based on student performance, selecting study material appropriately according to the student’s level of comprehension and previous knowledge.
Zhang and Liu (2008) [9] introduce the Tabu search logic in the Q-Learning algorithm function with the goal of balancing exploration and exploitation. Named T-Q-Learning, the convergence rate of this algorithm proves to be faster and avoids partially optimal solutions in experiments.
Javadi, Masoumi and Meybodi (2012) [10] suggest a method to improve performance of the learner model in tutoring systems. In the method proposed, the model of the student is determined by high level automata called Level Determinant Agents (LDA-LAQ), which attempt to characterize and promote the students’ learning model. LDA-LAQ employs learning automata as a learning mechanism in order to show how slow, normal or fast the student is in terms of learning ability.
Deepthi and Sasikumar (2014) [11] describe the learner model for an Intelligent Tutoring System in order to teach verb/noun inflection grammar rules of the Telugu language. In this work, the learner model is used to represent a student’s confidence level by applying each grammar rule, which is used by the tutor to generate problems, thus progressing in weak areas. A pilot study is conducted in order to measure the system’s effectiveness.
3. Simulation Methodology
3.1. ITS with Autonomous Model
In the simulation presented in this article, the Q-Learning algorithm (WATKINS, 1989) [8] is used to achieve Reinforcement Learning. In this algorithm, the choice of an action is based on a utility function that maps states and actions with a numeric value. In Guelpeli, Omar and Ribeiro (2004) [7], the utility value Q(s, a) of a pair (state(s), action(a)), is calculated from rewards measured by the quality of the learner’s cognitive state. Therefore, the main goal of the Q-Learning algorithm is to autonomously estimate, in each state the learner is found, the action with the greatest utility value. As a consequence, the system will be able to estimate the learner’s cognitive state.
The prototype used in the simulation does not know the models obtained, so the convergence occurs through optimal policy action learning, i.e., whatever was determined in the pedagogical policy. The experiments were conducted on a tutoring prototype, in an environment with a 5x10 matrix mapping states and actions (5 states and 10 actions) with the elements described below. A set of states S = {E0, E1, E2, E3, E4}, where each represents a possible cognitive state of the learner, in light of the interaction with the tutor, i.e. it is the result obtained by tutoring when applying action Ai in a given moment of time i.
Hence it is estimated that this learner possesses a cognitive degree based on these states, where:
E1 =>]2, 4],
E2 =>]4, 6],
E3 =>]6, 8],
E4 =>]8, 10].
A set of actions A = {A0, A1, A2, A3, A4, A5, A6, A7, A8, A9} can be chosen by the tutor. Each action may correspond to the application of tests, exercises, surveys, questions, assignments, exams, etc, or a combination of the former and other evaluation mechanisms, used by the tutor, according to established pedagogical strategies.
A set of Instant Rewards associated with each visited state, as follows:
E0 => R = 1 − Poor;
E1 => R = 3 − Regular;
E2 => R = 5 − Good;
E3 => R = 7 – Very Good;
E4 => R = 10 − Excellent.
A test for the methodology was defined in which three deterministic and non-deterministic models (M1, M2, M3) were created.
Two pedagogical policies P1 and P2 were created, where P2 is a more restrictive policy than P1 in relation to the model, since the intervals between actions are smaller. Thus more debugging of actions regarding states is possible and there will be a larger number of decisions for each state with the employment of policy P2.
Q-Learning produces an update in values Q in the direction maxa Qμt (st+1,a), generating the following algorithm:
Initiate Q(s, a).
For each instant t repeat:
1. Observe state st and choose action at according to the action policy (μ);
2. Observe state st+1 and update Qμt (st, at) according Qμt+1 (st, at) = Qμt (st, at)+αt [r(st)+γmaxaQμt (st+1,a)−Qμt (st,at)];
Until t equals a limit of steps.
Where we can define:
• Qμt+1 (st,at) – is the value (quality) of action a t in the state s t , following the action policy (μ).
• r(st) – is the immediate reward received in state st .
• α – is the learning rate.
• γ – is the discount rate.
• t – is a discrete sequence of moments in time; i.e., t = 0, 1, 2, 3, ...
• maxa Qμt (st+1,a) – Maximization policy with the greatest utility value in the future state.
• Factor γ(between 0 and 1) – the closer to 1, the greater the importance given to rewards that are more distant in time.
3.2. Tabu Search
Tabu search is a meta-heuristic search method created by Glover (1986) [12] and subsequently detailed in Glover and Laguna (1997) [13]. It is characterized by the construction of neighborhoods of possible solutions through the iterative routine that prohibits blocking in an optimal region.
From an initial solution, the TabuSearch algorithm explores a set of neighbor solutions at each iteration. The neighbor of the current solution with the best evaluation becomes the new solution, even if its evaluation is poorer. Figure 1 below presents an outline of the evolving process of generating neighbor solutions. The best neighbor represented by S∗i is considered as the current solution at each iteration.
The strategy of considering the best neighbor as the new solution is used to escape minimal regions, however it can cause the algorithm to form cycles. In other words, it can return to a solution that has already been adopted earlier through the same path. For instance, in Figure 1, if we consider that S*i is the current solution, the previous solution of iteration represented by S*i−1 will also belong to the region of the current solution. Thus if it is the best solution in the region, it will be adopted again as the current solution.
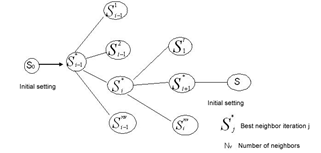
Figure 1. Neighbor generation plot for Tabu search. Source: (GLOVER; LAGUNA, 1997). [12]
The word Tabu (taboo) originated from the Polynesian island of Tonga and generally indicates a subject or behavior that is sacred and hence prohibited. The most important characteristic, reporting to its original meaning, comes from the idea that taboos are conceived from the social memory of forbidden subjects that undergoes change as time goes by. Therefore, in order to avoid cyclical occurrences, there is a list of forbidden movements called the Tabu list. In its most classical form, it contains the last movements that occur in a fixed size line, in which the first element that enters is also the last to exit. Tabu search thus excludes neighbors that are in the tabu list, even if they are good solutions in the current neighborhood.
3.3. Q-Learning Exploration Based on Tabu Search
According to Bianchi and Costa (2005) [14], an important trait of the Q-Learning algorithm is that actions used during the iterative process approximating function Q can be chosen using any exploration (or exploitation) strategy. A widely used strategy for choosing actions in Q-Learning implementations is the random exploration Ɛ - Greedy, in which the agent executes the action with the highest Q value with probability 1 - Ɛ, and chooses a random action with probability. This was the strategy implemented in Guelpeli, Omar and Ribeiro (2004) [7].
In this article, the meta-heuristic Tabu search was used as an exploration strategy. A set of Tabu lists was created:
LT = {T 0, T 1, T 2, T 3, T 4},
Where each list T S controls the choice of a solution (action A t) in a given state of learner S. The Tabu list is the FIFO (first in, first out) type; i.e., the first element to enter the list will be the first element to be removed when new elements are added.
The Tabu list can lead to the prohibition of solutions that are initially attractive to be visited, thus avoiding cycles in previously visited optimal locations and making it possible to visit an optimal result or close to global optimal. The aspiration criterion allows a tabu solution to be accepted only if the value of its goal function is greater than the best present solution. In this research, a memory structure was created to store whichever is the greatest utility value Q(s, a) yet achieved by the algorithm for a determined state-action pair (maxQ(s, a)). In this case, whenever a solution (action A) attends this aspiration criterion, it is adopted regardless if it belongs to the Tabu list.
The size of the region adopted in the simulation is the set of all available actions ({A0, A1, A2, A3, A4, A5, A6, A7, A8, A9}). The choice of the maximum size of the region is justified by the value Q(s t, a t) of each action that is previously known and available in the state-action plan matrix. In order to complete a minimum initial exploration of all actions available, each Tabu T S list starts with a maximum size of 9 elements. After reaching the maximum size of the list at each new insertion, this value is decremented until reaching the size tamanhoListaTabu. The simulations adopted the tamanhoListaTabu with 2 elements. The code below presents the pseudo-code of Tabu search as a Q-Learning algorithm exploration strategy:
Procedure choose_solution():
Generate initial solution;
If the solution is Tabu solution and does not attend the aspiration criterion:
Search for the best Tabu neighbor that attends the Aspiration criterion
If it is found:
Adopt solution;
If not:
Choose best neighbor that does not belong to Tabu list;
Adopt solution;
End if not
If not:
Adopt initial solution;
End if not
If solution does not belong to Tabu list:
Add solution to Tabu list;
End if
4. Results
In order to produce results, the non-deterministic learner model M 2 (Good) underwent simulations in 500 steps and the pedagogical policy adopted was P 1 (less restrictive). In each step, the value of the action quality Q(s, a) was selected. Each simulation was conducted 20 times and the results originated from the average of these simulations. The parameters used to update the value Q(s, a) were α = 0, 9 and γ = 0, 9. The percentage of exploratory actions was 20% of the simulation steps. After that period, the exploration phase of the algorithm is deactivated. The data presented in the graphs are generated from the values obtained in the simulation.
Figure 2 presents the comparison between the performance of the value of action quality Q(s, a) and the simulation with random exploration policy (Ɛ- Greedy) in relation to the meta-heuristic Tabu search presented in 500-step simulations:
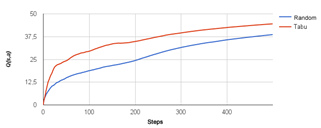
Figure 2. Comparison between exploration strategies – Graph - Q(s, a) - 500 steps.
Figure 3 presents the comparison between the performance of the Average Reinforcement with random exploration policy (E - Greedy) simulation in relation to the meta-heuristic Tabu search presented in simulations with 500 steps:
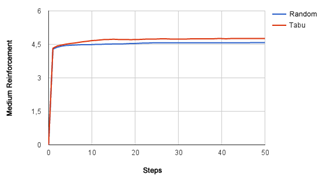
Figure 3. Comparison of exploration strategies - Graph – Medium Reinforcement - 500 steps.
The Wilcoxon signed-rank test (KERBY, 2014) [15] was chosen to test if the results obtained by simulations contain statistically relevant differences. The preference for this test was due to its paired characteristics and because the samples display abnormal distribution. The test confirmed that the performance obtained with both exploration policies in calculating action quality Q(s,a) (Figure 2) and Medium Reinforcement (Figure 3) differ with a confidence level of 95%.
Figure 4 and Table 1 display information regarding the percentage of visits to states E0, E1, E2, E3, E4 of both exploration policies:
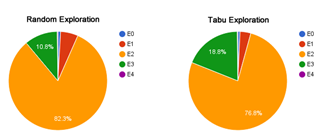
Figure 4. Comparison of exploration strategies – Percentage of state visits - 500 steps.
One may note that, while meta-heuristic exploratory search obtained 88.93% of visits in cognitive states E0, E1 and E2 and only 11.07% of visits in superior cognitive states E3 and E4, the insertion of meta-heuristic Tabu search obtained a percentage of visits in the three first cognitive states of 81.05% and reached a percentage of 18.95% in both superior cognitive states.
Table 1. Comparison of exploration strategies – Percentage of state visits - 500 steps.
| Estado | Aleatória | Tabu |
| E0 | 0,87% | 0,73% |
| E1 | 5,74% | 3,53% |
| E2 | 82,32% | 76,79% |
| E3 | 10,83% | 18,75% |
| E4 | 0,24% | 0,20% |
5. Conclusion
This article proposes the introduction of meta-heuristic Tabu as a Q-Learning algorithm exploration policy in ITS with autonomous learner model. Results indicate that the introduction of adequate meta-heuristics can increase learning speed and reach higher values in performance metrics the algorithm.
In simulations presented in this work, the introduction to Tabu search as a Q−Learning algorithm exploration policy resulted in an increase, with verified statistical relevance, in values of action quality Q(s, a), Medium Reinforcement, thus resulting in the learner having a higher percentage of visits to superior cognitive states in relation to random exploration policy.
The increase in convergence speed of the Q-Learning algorithm may optimize the use of the algorithm, thus reaching higher quality value for actions, and even render viable the use of Intelligent Tutoring Systems in environments in which there are seemingly no learner models available. The application and comparison of other meta-heuristics, both in the Q−Learning algorithm exploration phase and the in the exploitation phase, is suggested as further research.
References