Study the Spectral Properties of the Molecule Trimethyl Indium (TMIn) Using Semiempirical Quantum Programs

Hussain S. Akbar¹, Abdul Hakim Sh. Mohammed², Alaa A. Rauof¹

¹Physics Department, College of Science, Kirkuk University, Kirkuk City, Iraq

²Physics Dept., College of Education of Pure Science, Kirkuk University, Kirkuk City, Iraq

Email address

Citation

Hussain S. Akbar, Abdul Hakim Sh. Mohammed, Alaa A. Rauof. Study the Spectral Properties of the Molecule Trimethyl Indium (TMIn) Using Semiempirical Quantum Programs. American Journal of Materials Research. Vol. 3, No. 2, 2016, pp. 7-14.

Abstract

This study aims to determine the spectral properties of the trimethyl Indium molecule (TMIn) using the Semi-empirical quantum programs [HyperChem8.0, WinMopac7.21] by (MNDO-PM3) (Modified Neglect of Differential Overlap-Parameterization Model3). This method characterized by the flexibility, the simplicity and the quick performance. The equilibrium geometry and the potential curve were calculated and then from the curve, the total energy of the molecule at the equilibrium distance was calculated. In addition, the dissociation energy, the electronical energy, the core-core repulsion, the ionization energy, the zero point energy, the energy gap, the frequencies and basic vibrational modes have been calculated. The study’s results were in agreement with the previous research.

Keywords

Trimethyl Indium (TMI), Using MNDO PM3, Potential Energy, Equilibrium Distance

1. Introduction

The molecule trimethylindium TMIn (C₃H₉In) is a nonlinear organometalic molecule which is used as a source of Indium in the epitaxial processes of the crystals during the manufacturing process of the semiconductor materials by a method called (Metal Organic Chemical Vapor Deposition) (MOCVD) to form semiconductors containing indium compounds such as AsIn. Additionally, TMIn can be used in manufacturing of light emitting diodes, emitting lasers, high-power solar cells and high-efficiency transistors. However, TMIn is a pyrophoric (ignites spontaneously upon contact with air) therefore it should be treated with caution [1].

One of the most basic physics and chemistry matters is finding the molecular properties such as the energy and the balanced molecular arrangement, which would be in agreement with the quantum mechanics and the Schrodinger equation:

Ĥ Y = E Y                                                            (1)

Where Ĥ is Hamiltonian-Operator which is characterizes the total energy of any wave function for a system in a certain level. E is the numerical value of energy. Y is the wave function of the quantum system and describes the system status.

It is known that Schrodinger equation solution can be fully possible for the hydrogen atom only, while it will be uncompleted and the full solution cannot be obtained for any other molecular system. Therefore approximate solutions can be acquired and then they

can be improved gradually to approach the general solutions as much as possible [2].

The theoretical chemistry programs can be defined as the science which concern with the application of the theoretical foundations and solving the mathematical problems. The molecular modeling program is one of the applications of these programs which can predict and find a number of important physical properties.

The ways of determining the total energy to predict molecular structures are: - [3, 4]

1.   Ab-initio electronic structures calculations.

2.   Semiempirical methods.

3.   Molecular mechanics.

4.   Density functional theory.

The theoretical calculations of the first type depend on the quantum mechanics. It is consider as one of the advanced methods in this area because of their high precision and for using set of rules to solve Schrodinger equation for different chemical systems. But this method is still have limited applications due to the long time that required for obtaining the calculations which sometimes exceed several weeks for each molecule as it will need to deal with the whole internal electrons in the molecule. The calculations of the second type are using the quantum mechanics and rely on the valence electrons only as the inner electrons covers part of the core of the atom and the nucleus. While the third type method’s calculations depend on the principles of classical physics, which eliminates the processors of the electronic arrangement for the material. Therefore, it has limited application in such studies. The fourth type also depends on the quantum mechanics in their solutions but it deals with the electronic density.

(HyperChem8.0, WinMopac7.21) is considered as the most important molecular modeling program. Hyperchem is a quantum mechanics program contains all the molecular modeling programs. Through this program, it is possible to draw the molecules by selecting the internal coordinates of the molecules (r, θ˚, φ˚) and then predicting their spectral properties. On the other hand, WinMopac7.21 program is an improved copy of MOPAC programs which is constantly evolved. In fact this program presented a big effort in the field of the scientific research. It is a semi-empirical program and provided precise solutions for the experimental difficulties during the study of some hazardous materials, highly sensitive or very active materials [5].

In (2001) [6], B. H. Cardellino and his group studied the theory of indium compounds and calculated engineering, electronic and thermal properties by using the method of ab initio and of these compounds: halides indium and Hydride [InF-InCl-InCl₃-InH-InH₂], methyl indium, Dimethyl indium hydrogen and derivatives [In(CH₃)-In(CH₃)₂H-In (CH₃)₃H₂], trimethylindium, trimethylindium with ammonia and trimethylamin [In (CH3)₃- (CH3)₃ In: NH3- (CH₃)₃In: (NH3)₃]. In (2006) [7], A. Deleon studied the shape of the molecule and the spectral frequencies of glucose and fructose molecules using a semi-empirical and DFT methood. In 2010 [8], Nayef studied the thermal properties of (GaAs) molecule using semi-empirical quantum programs via the method MNDO-PM3 at a stable geometric structure. In 2014 [9], R. Benallal studied the comparison of the stability and properties of vibrational spectra for some flavonols compounds by quantum mechanical calculations [smiempirical method (ZINDO/1, PM3 and ZINDO/S) and calculated standard enthalpy of formation, vibrational spectra, binding energy, and dipole moment. In 2015 [10], R. Benallal studied experimental and theoretical of the structural and spectroscopic properties of Quinoxalin-2[1H]-one molecule at room temperature in its ground state and this study is complemented by calculations of conformational, charge distribution, energy properties and electronic transitions positions of the molecule in the ground state using AM1 and ZINDO semi- empirical methods.

This project aims to study the spectral properties and the molecular structure of TMI molecule (C₃H₉In) in the infrared region (IR), by using the semi-empirical calculations via the method (MNDO-PM3). This study also aimed to find the lower energy of the stable state of the molecule via the potential energy curves. The study of the spectral and thermal properties of the two molecules [trimethylaluminum TMAl, trimethylindium TMIn] using semiempirical quantum programs have been investigated in ref. [11].

2. Theory

The atomic spectrums are lines resulting from the electronic transitions between the energy levels of the atom, while the molecular spectrums appear in the form of a wide spectrum consisting set of lines arise from a number of electronic transitions when analyzed with a high definition analyzer [12].

There are many types of molecular energy states which are the Rotational Energy Levels (, the Vibrational Energy Levels (, and the Electronic Energy Levels (

                      (2)

The differences between the electronic energy levels are much greater than the differences between vibrational energy levels, where these in turn are much larger than the rotational energy levels.

This research is focusing on the vibrational energy as it represents the potential energy and the kinetic energy that possessed by the molecules. This energy is quantization energy and become from the vibrational movements of the molecule. The vibrational movement can be studied classically for a diatomic molecule in term of one dimensional harmonic model as initial approximation providing a successful start to discuss the vibratory motion for diatomic molecules. In order to approximate, we can imagine that there are two atoms linked by a chemical bond and vibrate along inter nuclear axis. If the two atoms have the masses m₁ and m₂ and the bond between them has zero mass helical spring, the two atoms would vibrate harmonically to the center of the mass. According to the Hook law the restoring force is [12]:

                             (3)

Where (k) is the force constant, (r-re) is the displacement from the center of the mass.

Both masses can move together as one mass and so they can be reduced to (μ):

                             (4)

The classical frequency of the vibrant is given as the following relationship:

                            (5)

Where () is the vibration frequencies. Therefore, the relationship between the vibrational potential energy and the distance can be represented by the typical energy equation [12, 13]:

                         (6)

Where  is the potential energy by the harmonic model. According to quantum mechanics, the Schrodinger equation can be representing as follows [12]:

                   (7)

It is obvious from solving this equation that the total vibrational energy is quantitative and take the values:

, v = 0, 1, 2                    (8)

Where  is the total vibrational frequency and (v) is the number of the vibrational quantum. (1/2 hν_vib) is the smaller energy value when v = 0 and called as the zero point energy, and this value represents the difference between the classical mechanics and the quantum molecular vibrations. However, the energy in the classical mechanics can be equal to zero and this means that the molecule is not having a vibrational energy at the normal circumstances, while the quantum mechanics confirms that the molecule must have a certain vibration.

The energy levels can be expressed by the unit of cm^-1, so the value of the reduced vibrational energy levels can be represented by the unit cm^-1 after dividing on (hc) as in the equation:

                            (9)

Where G (v) represents the vibrational energy level, Where ω is the wavenumber and the unit is cm^-1. The differences between the vibration energy levels by the harmonic oscillator model are equal to the value of one.

In fact, the real diatomic molecules do not behave harmonic accurately, because when the value of (r-r_e) is very small, the particles act harmonically and by increasing the displacement, molecules begin to deviate from harmonic behavior and act as an harmonic oscillator until reach a specific value where the molecule dissociate to their constituent atoms. The potential energy at this point can be identified as the dissociation energy (De). For this reason, many potential functions were proposed consistent better with the experimental curve. Morse potential function is one of these functions and is represented by the following equation [12]:

                       (10)

Where  represents the potential energy of the bond and () is the dissociation energy of the molecule and b is a special constant for each electronic state of the molecule.

When the potential energy is substituted with the Morse potential function in Schrorodinger equation, the vibration energy levels equal to:

               (11)

Where () is the vibrational frequency in anharmonic movement and () is the anharmonic constant. The zero point energy as anharmonic model when (v = 0) is:

                 (12)

It can be also calculated the vibrational frequency and the normal coordinate from the molecular energy constants which is the most common way. So Wilson equation can be solved [14]:

                      (13)

Where F_ij is the Matrix element energy constants, λ is the eigenvalue, M_ij is the atomic mass matrix element and L_j is the combination transaction values. Solving this equation is a fundamental to find the determinate roots(l) and to evaluate the vibrational frequency and to locate the eigenvectors that determine the normal coordinates. The dipole moment is an electrostatic force operating between two equal and different charges.

The spectra of vibrational motion of multiple molecules of atoms be complex, where vibrational movement can be described in terms of a simple movements are called normal mode of vibration as base (3N-6) for nonlinear molecule [15].

If the amount of charge is q and the distance between two of them is d, the equation of the dipole moment can be written as [16]:

μ = q.d                                      (14)

3. Results & Discussion

3.1. The Molecular Structure

TMIn can be represented by the shape in the figure 1, which was drawn by Hyper Chem8.0 program. The calculation of the program depends on the internal coordinates (r, θ, φ) and on the geometric shape at the equilibrium state.

Table 1 shows TMIn molecule initialize matrix which can be obtained after drawing the molecule when reaching the optimization state for the best geometrical position. The table illustrates the atoms of the molecule, the distance between these atoms (r), the best position of these atoms (Opt.), the values of the angles between bonds (θ˚) and the dihedral angles (φ˚).

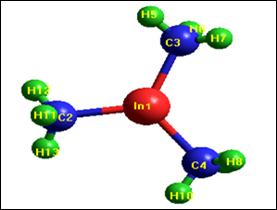
Figure 1. The molecular structure of TMIn molecule drawn by the HyperChem 8.0 program.

Table 1. The initialize matrix, the internal coordinates (r, θ˚, φ˚) and the symmetry of the atoms sites (A, B, C) of TMIn molecule at the stable state calculated by HyperChem program.

Table 2 shows the obtained results from the present study for the internal coordinates of the TMIn molecule between the two atoms of In-C1. It was clear the rapprochement of the theoretical values with the previous studies values.

Table 2. The dimensions, the angles and the surface angles of the TMIn molecule calculated by the HyperChem program and compared with the experimental results of other work.

Table 3 illustrates some of the spectral properties that give full descriptions of the molecular structure. These properties were found after obtaining the initialize matrix and were incorporated into the matrix by using the WinMopac7.21 program. These properties include the total energy at the stable position, the electronic energy, the core-core repulsion energy, the zero point energy, the ionization energy, the dipole moment, molecular weight and the numbers of the occupied levels with electrons.

Table 3. The results of the spectral properties of the TMIn molecule calculated by the (WinMopac7.21) program.

3.2. The an Harmonic Potential Energy Calculations

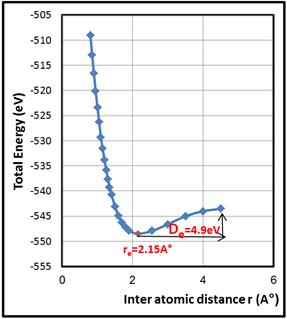
Figure 2. The total energies of the TMIn molecule at different (In – C2) lengths.

Figure 2 illustrates the relationship between the total energy and the distance between the two atoms (In-C2). The potential energy curve of the molecule is plotted by changing the In-C bond length and calculating the total energy each time as making the bond fixed by making Opt. = 0 instead of 1. The curve showed that the lowest value of the total energy is (-548.49 eV) at the equilibrium distance (r = r_eq = 2.15A°). The curve also showed that the energy increase steadily after the equilibrium distance until the bond dissociates at (De = 4.9 eV) which represents the difference between energy Molecule in the case of default equilibrium and energy Separate atoms of each. This value was in agreement with the literatures (De = 2.69 eV) [18].

The curve in the figure 2 showed that when the atoms are bringing closer to each other, less than the balanced distance, a high repulsion force arise accompanied by an increasing potential energy. In contrary, when the atoms diverge, more than the balanced distance, a weak attraction force appear accompanied by a weak potential energy that increases slowly until the bond breaking down. This can be called dissociation energy.

3.3. The Frequencies and the Vibrational Modes Calculation

Table 4 illustrates the basic vibrational frequencies at the infrared (IR) region of the TMI molecule with the intensity and the symmetry as their number was (33) according to the relationship (3N-6) where N represents the number of atoms of the molecule. The table also showed that the frequencies (the wavenumbers) of HyperChem and WinMopac programs are close with the literatures measures. It has been concluded that the vibrational frequencies between the two atoms (In-C) were at the wavenumbers 509.37 cm^-1. This was in agreement with the practical measures 500 cm^-1 [19].

Table 4. The vibrational frequencies of TMIn calculated by HyperChem and WinMopac programs and compared with the practical values of other works.

*Abbreviations: vw; very weak; m. medium; s. strong; ms, medium strong

It has been also observed that the highest absorption intensity was at the wavenumber 776.74 cm^-1 as shown in figure 3, This value was in agreement with the experimental values[19].

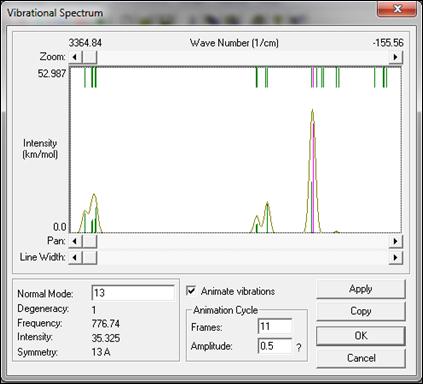
Figure 3. The absorption intensity of TMIn drown by HyperChem8.0 program.

Figure 4 illustrates some of the vibrational modes of the TMIn molecule and shows that the atoms motion directions which represented by the arrows, and also determines the intensity, symmetry and the frequency for each modes.

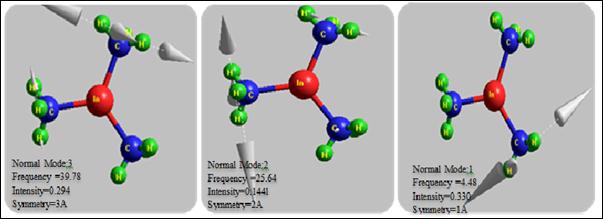
Figure 4. The main vibrational modes, the frequency, the intensity and symmetry of TMIn for each mode drown by HyperChem8.0 program.

3.4. Molecular Orbital Eigenvalues

Figure 5 illustrates the energy levels of the molecular orbitals and the symmetry of each level for the TMIn treated via HyperChem program. The values of the energy levels of the TMIn molecule and clarifying the higher occupied molecular orbital (HOMO) and the lower unoccupied molecular orbital (LUMO) calculated by the HyperChem program.The figure shows 12 of the occupied orbitals and 13 of the unoccupied orbitals. The energy of the higher occupied molecular orbital (E_HOMO) and the energy of the lower unoccupied molecular orbital (E_LUMO) were calculated by measuring the molecular orbital eigenvalues.

Figure 5. The values of the energy levels of the TMIn molecule and clarifying the higher occupied molecular orbital (HOMO) and the lower unoccupied molecular orbital (LUMO) calculated by the HyperChem program.

The gap energy was also calculated according to the relationship (E_gap = E_LOMO- E_HOMO), and was equal to 10.72 eV. The ionization energy (I.P) was calculated from the absolute value of the highest occupied orbital and it was equal to 10.33 eV.

4. Conclusions

From studying the molecular properties of the molecule, it has been concluded that:

1.   The absorption intensity between the two atoms (In-C) were at the wavenumbers 509.37 cm^-1, The vibrational frequencies depend on the masses of the vibrational atoms as the lighter atom would have the highest vibrational frequency, according to the equation (5).

2.   The study was found that the equilibrium distance (bond length) of TMIn is (2.15 A°) and the total energy is (-548.49 eV) whereas the dissociation energy is (4.9 eV).

3.   The molecule has 12 orbitals occupied by the electrons and 13 orbitals unoccupied by the electrons. The energy gap was 10.72 eV and the ionization energy was (10.34 eV).

4.   The value of dipole moment of TMI molecule was 0.176 D where the dipole moment is a function of the charge and the bond length as the equation (14).

References

1. V. Shenai Deodatta; L. Timmons Michael; L. Dicarlo Ronald; J. Marsman Charles (2004). "Correlation of film properties and reduced impurity concentrations in sources for III/V-MOVPE using high-purity trimethylindium and tertiarybutylphosphine", Journal of Crystal Growth 272: 603. doi:10.1016/j.jcrysgro.2004.09.006.
2. A.Donald M.c. Quarrie; "Quantum Chemistry", University Scince Books, Oxford University press 1983.
3. H. Dorsett and A.White" Overview of Molecular Modeling and Ab-initio Molecular Orbital Methods Suitable for use with Energetic Materials", DSTO Aeronautical and Maritime Research Laboratory Commonwealth of Australia 2000.
4. H. Eschrig, "The Fundamentals of Density Functional Theory(revised and extended version) " Dresden, August 2003.
5. J. J.P.Stewart and F. J.Seiler," A Semiempirical Molecular Orbital Program", Research Laboratory U. S. Air Force Academy Colorado Springs, CO 80840 (U.S.A.) March, 1990.
6. B. H. Cardelino, C. E. Moore, C. A. Cardelino, D. O. Frazier, and K. J. Bachmann, "Theoretical Study of Compounds of Interest for Organometallic Chemical Vapor Deposition", J. Phys. Chem. A 2001, 105, 849-868.
7. M. Ibrahim, M. Alaam, H. El-Haes, A. F. Jalbout, A. de leon, "Analysis of the structure and vibrational spectra of glucose and fructose", volume 31, numero3, 2006.
8. H. A. Naif, "Study the thermal properties of (GaAs) semiconductor laser by using Quantum Mechanics Semiempirical method", Physics Department, College of Science, Al-Mustansiriyah University 2010.
9. H. G. Jasim, "Comparison Study of the Stability and Properties of Vibrational Spectra For Some Flavonols Compounds by Quantum Mechanical Calculations", Journal of Kufa for Chemical Science No. (9), (2014).
10. R. Benallal1, B. Azize1, T. Sahdane1, H. Bougharraf1, A. Laghrabli1, B. Kabouchi1, M. Elfaydy, L. Lakhrissi, B. Lakhrissi, E. M. Essassi," Experimental and theoretical study of the structural and spectroscopic properties of Quinoxalin-2[1H]-one molecule at room temperature in its ground state", J. Mater. Environ. Sci. 6 (3) (2015) 682-685.
11. H. S. Akbar, A. Sh. Mohammed, A. A. Raouf, "Study the spectral and thermal properties of the two molecule [trimethylaluminum TMAl,trimethylindium TMIn] using semiempirical quantum programs], M.Sc. Thesis, Kirkuk University, Physics Dept., College of Science (2016).
12. G.M. Barrow, "Introduction to Molecular Spectroscopy" McGraw- Hill, 1962.
13. F. A. Cotton, (1971). Chemical Applications of Group Theory (2nd ed.). New York: Wiley. ISBN0471175706.
14. G. Henderson, D. Neuville, R. Downs "Spectroscopic Methods in Mineralogy and Material Sciences", Reviews in Mineralogy & Geochemistry, Vol. 78 pp. 509-541,2014.
15. G. Hezberg, ''Molecular Spectra and Molecular Structure Infrared and Raman Spectra of polyatomic Molecules'', Van Nostrand Reinhold Co. NewYork (1971).
16. B. Schrader, ''Infrared and Raman Spectroscopy'', VCH Publishers Inc NewYork, (1995).
17. J. O. Cox, G. Pilcher, "Thermochemistry of Organic and Organometallic Compounds" Academic Press, New York, N.Y., (1970).
18. B. H. Cardelino, C. E. Moore, C. A. Cardelino, S. D. McCall, D. O. Frazier, and K. J. Bachmann, "Semiclassical Calculation of Reaction Rate Constants for Homolytical Dissociation Reactions of Interest in Organometallic Vapor-Phase Epitaxy (OMVPE) ", J. Phys. Chem. A 2003, 107, 3708-3718.
19. J. Weidlein, "Gmelin Hanbook In Organoindium Compounds",4,442, Springer-Verlage Berlin Heidelberg GmbH 1991.