Probabilistic Limit Equilibrium Analysis of Pile in Two-Layer Laterally Spreaded Soil
Reda Farag1, 2
1Department of Civil Engineering, Qassim University, Almulyda, Kingdom of Saudi Arabia
2Housing and Building Research Center, Department of Structures and Metallic Construction, Giza, Arab Republic of Egypt
Email address
Citation
Reda Farag. Probabilistic Limit Equilibrium Analysis of Pile in Two-Layer Laterally Spreaded Soil. International Journal of Civil Engineering and Construction Science. Vol. 3, No. 1, 2016, pp. 8-15.
Abstract
Because of its critical effect and significant destructive nature during and after the seismic events, the lateral ground spreading has seen an increasing interest in the geotechnical earthquake engineering. This paper introduces a quick method to predict pile-failure under lateral spread. The method integrates the limit equilibrium method (LEM) with the second order reliability method (SORM). In the procedure, the Finite element method (FEM), is used to build up a limit equilibrium, LE-based finite element model. This model is coupled with (SORM) via the response surface method (RSM). In the finite element model the soil is represented by 3D solid elastoplastic (Drucker-Prager failure criterion) while the pile is represented by elastic 3D beam element. The proposed method is validated using Monte Carlo Simulation (MCS). Numerical examples are used for further illustration. Both operational and structural limit states are used. For the considered example, the soil pressure and the radius of pile are found to be the most sensitive variables.
Keywords
Pile Foundation, Two Layer Soil System, Lateral Spread, Limit Equilibrium, Probability of Failure
1. Introduction
The seismic behavior of pile foundation embedded in liquefiable soil is complex due to complicated nonlinear dynamic soil-pile interaction; progressive built up of pore water pressure and an almost complete loss in soil stiffness and strength. Assessment of this complex seismic response taking into account the effect of uncertainties in the input ground motion and properties of soil-pile system, requires the use of seismic effective stress analyses with sophisticated constitutive models; multiple model parameter values and multiple input ground motion [1,2]. Such rigorous assessment prompt the researchers to gather high quality field data for constitutive model calibration, develop advanced computational techniques, prepare, perform and interpret the analysis.
Because of the abovementioned complexity, it is desirable to develop a rational method of estimating the response of pile that can reliably predict the pile performance in order to avoid structural or operational failure of the foundation. Strictly speaking, the performance of 3D elastoplastic rational analyses of the liquefied ground response during shaking, taking into account the soil-pile interaction are certainly possible today [3-5], however they are still considered well beyond limits for common applications in practice. As a consequence, the probabilistic analysis is performed using one of the simplified pseudo-static methods. In these methods, the loads or displacements applied by the laterally spreading ground are being estimated independently, from empirical relationships, and subsequently applied as external loads to the pile. The pseudo-static methods may be divided in two categories; the P–y method (nonlinear load–displacement (P–y) relationship) [6] and the Limit equilibrium Method [7].
Recently, a probabilistic procedure has been suggested by Bradley and his co-workers [8]. In the procedure, the pseudostatic, first category (P-y method) is coupled with the MCS. The pseudo-static model involves applying static displacements and forces to a typical beam-spring model. It has been reported that uncertainties in the Pseudostatic analysis result in significant uncertainty in the two basic components of pile response; the maximum moment developing along the pile and the associated maximum pile deflection. Therefore, it is stressed that a single reference model is potentially erroneous.
To the author`s knowledge, the above mentioned probabilistic framework is the only probabilistic method in the literature to determine the reliability of a pile under lateral spread. As an alternative method to this simulation-based method, the present paper introduces a gradient based method. In the proposed method, the principles of the (LEM) are applied to a Finite Element, FE-model which is coupled with the (SORM) using the (RSM). In the LE-based FE model, the soil is represented by 3D solid elastoplastic (Drucker-Prager failure criterion) while the pile is represented by elastic 3D beam element. The suggested methodology is verified and elaborated using numerical examples. Both operational and structural limit state are studied. Furthermore, the most sensitive variables are determined. In one computer session, the computed damage of the piles in the numerical analysis can be compared to the actual damage observed in the field inspection. The method is simple and is implemented using common commercial programs.
2. Design Cases of Piles in Laterally Spreading Ground
In the last decades, many of research works and studies have been focused on lateral spreading loads due to a liquefying layer with or without an upper non-liquefiable stratum. In practice, two design cases are generally encountered; two-layer soil profile and three-layer soil profiles. In the two-layer soil system, the non-liquefiable layer is either under the liquefiable layer as a bed stratum or above it as a shallow crust, i.e, floating pile, see Figure 1-a. In this case the pile is embedded in the non-liquefiable layer and acts as a cantilever beam. While in the three layers soil case, the liquefiable layer is confined between the two non-liquefiable layers, the crust and the bed, as shown in Figure 1-b. The two-layer soil system is studied in the present paper while the three-layer soil system is analyzed in another one [9].
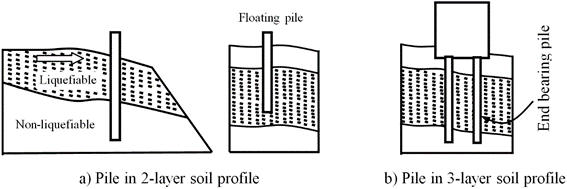
Figure 1. Pile foundation in laterally spreading ground.
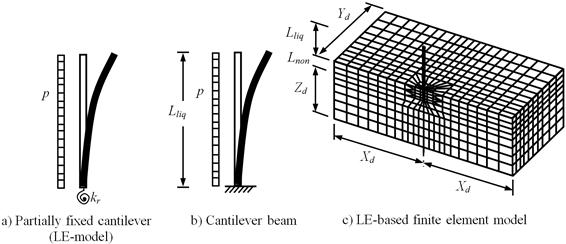
Figure 2. Models of 2-Layer Soil Profile.
3. Limit Equilibrium Model
Dobry and his co-researcher [7], have proposed and calibrated a LEM. According to this method, the pile in two-layer soil system behaves as a partially fixed cantilever beam of length equals to the thickness of the liquefied layer, Lliq, and is subjected to an assumed uniform distributed load, pDP, where DP is the pile diameter and p= 10.3 ±1.5 kPa, is an assumed uniform pressure perpendicular to its axis. The cantilever has a spring of rotational flexibility kr = 5738 kN m/rad, which represents the flexibility of the bottom non-liquefiable layer, as shown in Figure 2-a. It has been reported that, the LE-model predicts the pile response with good agreement between predicted and observed performance. In other words, the applicability of the above values measured in the centrifuge tests to the field are confirmed for a range of pile and liquefied soil conditions. For the LE-model, the moment, M and the drift, ux can be expressed as:
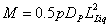 (1)
(1)
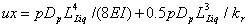 (2)
(2)
where: E is the pile elastic modulus and I is the pile second moment of inertia. The other variables are defined before. If the bed layer is a rock layer and the pile is sufficiently fixed in it, the LE-model becomes a simple cantilever beam, as shown in Figure 2-b. In this situation, the moment remains as in Eq. (1), while the pile head deflection, (ux) is expressed as in the elastic beam theory.
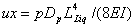 (3)
(3)
where: the variables are defined before.
Proposed LE-Based FE Model
In the present work, the LEM is coupled with the (SORM) to extract a quick estimation of probability of failure, Pf. To incorporate the soil nonlinearity into consideration, a LE- based finite element model is built up. Then it is integrated with SORM via the RSM. In this model, the non-liquefied layer is represented by a three dimensional nonlinear elasto-plastic (Drucker-Prager) element, while the pile is presented by elastic three dimensional beam elements subjected to the soil pressure (p). The Drucker-Prager element is defined in the in hand FE-program (COSMOS 2000 [10]) using four parameters; the angle of internal friction (j); soil cohesion (c); elastic modulus of soil (Es) and the soil density (gs). The LE-based finite element model is shown in Figure 2-c, where, Lnon the thickness of non-liquefied layer, Xd, Yd and Zd, are distances in the space those represent the soil domain of interest.
4. Response Surface Methodology
The reliability evaluation using the gradient-based methods, first or second order reliability method, FORM/SORM, requires that the limit state function to be available in an explicit form. This requirement is not available for complex structural system like soil-pile system under lateral spread. This obstacle is overcome using the response surface method which approximates the response in an explicit form. For this propose linear or quadratic polynomials are usually used as in Eq. (4) and Eq. (5). The linear polynomial Eq. (4), is usually used in preliminary analysis as it is seen in the examples.
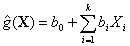 (4)
(4)
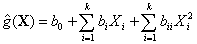 (5)
(5)
where Xi (i = 1, 2,¼, k) is the ith random variable, and b0, bi, and bii, are unknown coefficients to be determined from the deterministic analyses of the problem at specific data points, commonly known as experimental sampling points.
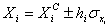
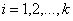 (6)
(6)
where 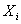 is the coded ith variable,
is the coded ith variable, 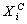 and
and 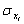 are the coordinates of the centre point and the standard deviation of a random variable Xi, respectively;
are the coordinates of the centre point and the standard deviation of a random variable Xi, respectively; 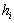 is an arbitrary factor that defines the experimental region, and k is number of random variables in the formulation [11].
is an arbitrary factor that defines the experimental region, and k is number of random variables in the formulation [11].
Selection of the center point around which the sampling points are selected is the next task in RSM. The initial center point 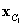 is selected to be the mean values of the random variable Xi’s. Then, using the values of g(X) obtained from the deterministic FEM evaluations for all the experimental sampling points around the center point, the response surface
is selected to be the mean values of the random variable Xi’s. Then, using the values of g(X) obtained from the deterministic FEM evaluations for all the experimental sampling points around the center point, the response surface 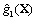 can be generated explicitly in terms of the random variables, X. Once a closed form of the limit state function,
can be generated explicitly in terms of the random variables, X. Once a closed form of the limit state function,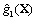 , is obtained, the coordinates of the checking point
, is obtained, the coordinates of the checking point 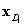 can be estimated using FORM/SORM, first or second order reliability method. The actual response can be evaluated again at the checking point
can be estimated using FORM/SORM, first or second order reliability method. The actual response can be evaluated again at the checking point 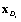 , i.e., g(
, i.e., g(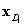 ) and a new center point
) and a new center point 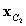 can be selected using linear interpolation from the center point
can be selected using linear interpolation from the center point 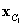 to
to 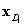 such that g(X) = 0; i.e.,
such that g(X) = 0; i.e.,
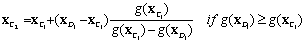 (7)
(7)
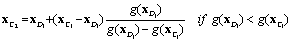 (8)
(8)
where, 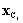 and
and 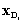 are the centre and design points, respectively, in the ith iteration, and
are the centre and design points, respectively, in the ith iteration, and 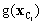 and
and 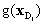 are the response surface values at centre and design points, respectively. This iterative scheme can be repeated until a pre-selected convergence criterion of
are the response surface values at centre and design points, respectively. This iterative scheme can be repeated until a pre-selected convergence criterion of 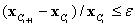 is satisfied. The convergence is satisfied in the last iteration. In the present work, ε is considered to be |0.05|.
is satisfied. The convergence is satisfied in the last iteration. In the present work, ε is considered to be |0.05|.
5. Statistical Description of Random Variables
The piles can be made of different materials. In the present work, piles of reinforced concrete or Polyetherimide ULTEM 1000, -used in centrifuge tests- are used in the analysis. The pile parameters are considered to be random; modulus of elasticity of the pile, (E), the external radius (r) and thickness (t). Besides the pile unit density (g) and Poisson’s ratio (v) as in (NBS) [12]. On the other hand, the soil elastic modulus (Es), the cohesion strength (c), the angle of internal friction (j), the soil unit density (gs) and the soil Poisson’s ratio (vs) are considered to be random variables (JCSS) [13]. The uncertainty in the lateral displacement depends on the uncertainties in both soil properties and the earthquake characteristics including accelerations, time histories, duration, etc. In the present work, both the lateral displacement and the soil pressure (p), are assumed to follow the probability distribution of extreme value Type 1 (EV-I) distribution. For all the design related variables, the statistical characteristics are gathered from the literature for each example.
6. Pile Limit State Function
As it is well known, the lateral spreading can cause failure of the pile in either ultimate or serviceability performance, i.e., when the allowable strength or the allowable lateral drift is violated. In the present study, both the flexural strength and lateral drift limit states, denoted hereafter as 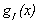 and
and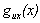 , respectively, are considered:
, respectively, are considered:
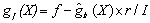 (9)
(9)
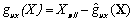 (10)
(10)
where, f and Xall, are the characteristic strength of the pile material and the allowable drift, respectively, and 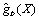 and
and 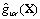 are the bending and drift response surface functions, respectively.
are the bending and drift response surface functions, respectively.
7. Numerical Examples
The suggested method is verified, implemented and further elaborated with the help of three examples. The three examples are called namely; pile embedded in rock bed; Centrifuge Test Model and Limit Equilibrium Finite Element model, (LEFE). The results are validated using Monte Carlo simulation Method as it is seen hereafter.
7.1. Example 1: Pile Fixed in Rock Layer
An assumed reinforced concrete (RC) pile of radius r = 30 cm is driven in a liquefiable layer and embedded in a rock bed layer (sufficiently deep to assure fixity). The thickness of the liquefiable soil layer LLiq=7.00 m. The lateral spread is represented as an assumed uniform distributed pressure, p=10.5 kN/m2. The system variables are assumed to be uncertainties with statistical properties which are gathered from the literature [12,14] and listed in Table 1.
According to the limit equilibrium method, the above pile behaves as a fixed cantilever beam subjected to pressure p = 10.5 kN/m2, as shown in Figure 2-b. Assuming the allowable drift is Xall = 5 cm, the limit state can be obtained by substituting Eq. 3 in Eq. 10:
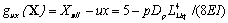 (11)
(11)
Using Monte Carlo simulation, the probability of failure and the safety index are found to be Pf-MCS =1.40×10-3 and b-MCS=2.196, respectively. These values are considered as reference values. Re-computing them again using FORM/SORM, they are found to be; 1.38×10-2, 2.203, 1.42×10-2, 2.191, respectively, as listed in Table 2. The variable sensitivities are also listed in the Table.
Table 1. Statistical Characteristic of Random Variables - Example 1.
| | Random variables | Symbol | Distribution | Nominal | Mean | COV | Reference |
| 1 | Lateral pressure | p | EV-I | 10.50 kN/m2 | 10.50 | 0.45* | * |
| 2 | Radius | r | LN | 0.30 m | 0.30 | 0.10 | [14] |
| 3 | Length | LLiq | N | 7.00 m | 7.00 | 0.04* | * |
| 4 | E-modulus of R.C. | E | LN | 2.0×107 kN/m2 | 2.01×107 | 0.18* | [12] |
* Data not available. Assumed parameters are based on engineering judgment.
Table 2. Results of Reliability Analysis- Example 1.
| | | Variables sensitivities | β | Pf | No. of function calls |
| | | p | r | E | LLiq |
| | i) Explicit limit state | | | | | | | |
| 1 | Monte Carlo simulation* | | | | | 2.196 | 1.40×10-2 | 105 |
| 2 | FORM | -0.696 | 0.592 | 0.306 | -0.268 | 2.203 | 1.38×10-2 | 1 |
| 3 | SORM | -0.696 | 0.592 | 0.306 | -0.268 | 2.191 | 1.42×10-2 | 1 |
| | ii) Response surface | | | | | | | |
| 4 | FORM | -0.591 | 0.697 | 0.311 | -0.262 | 2.183 | 1.45×10-2 | 9 |
| 5 | SORM | -0.591 | 0.697 | 0.311 | -0.262 | 1.938 | 2.63×10-2 | 9 |
Then, the response surface is performed using the quadratic polynomial function, Eq. (4), and following the iterative scheme, the drift is represented by the following limit state function:
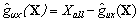
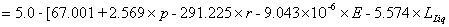
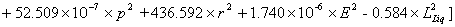 (12)
(12)
Using FORM and SORM, the safety-index is found to be 2.183 and 1.938 (11.5% and 0.6% less than b-MCS). It can be noted that the variables importance are found to be 59.1%; 69.7%; 31.1% and 26.2% for the soil pressure (p), pile radius (r); pile elastic modulus (E) and the thickness of the liquefied layer (LLiq), respectively. In other words, the sensitivities of the variables using the response surface function are similar to those resulted using the explicit limit state function.
7.2. Example 2: Model of Centrifuge Test
An 8 m- pile length is derived in a 6 m layer of liquefiable sand overlaying a 2 m layer of non-liquefiable sand. The pile has a circular section of radius 30 cm and has a bending stiffness EI=8000 kNm2. This example is the actual model of a centrifuge test model (3) performed by Dobry and his co-workers [7]. The pile is manufactured of Polyetherimide ULTEM 1000. Assuming that the modulus of elasticity and the flexural strength E= 3300 and f = 1600 MPa, respectively, the pile thickness is found to be t = 3.4 cm, (ULTEM ® PEI Resin Product Guide Eng/6/2003 CA). The statistical characteristics are summarized in Table 3, [14]. The Table involves rotational flexibility kr = 5738 kN m/rad and the applied pressure p = 10.5 kN/m2., of the partially fixed LE-model.
Assuming the allowable drift is assumed Xall = 50 cm, the limit state can be obtained by substituting Eq. 2 in Eq. 10:
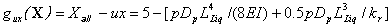 (13)
(13)
7.2.1. Monte Carlo Simulation
Calling the limit state function in risk calculation, it is found that the safety index in case of Monte Carlo simulation, b-MCS =2.236and in case of second order reliability method, b-SORM=2.235, respectively. These values are calculated using six random variables as shown in Table 4, and these values represent reference values.
7.2.2. Preliminary Response Surface-Based Analysis
In reliability analysis using RSM, it is a good practice to perform a preliminary analysis using the first order polynomial, Eq. (4). This is particularly when the number of variables is large. This example has a relatively large number of variables, k = 6. Therefore, a sensitivity analysis is carried out. It is found that, the pile elastic modulus and the pile thickness, E and t (have low sensitivities 5.4% and 3.7%; respectively). Consequently, they are considered as deterministic variables, reducing the number of variables to four variables. The results of preliminary analysis is shown in Table 4
7.2.3. Response Surface
Using the quadratic polynomial, the following response surface function is obtained.
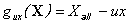
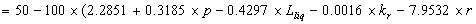
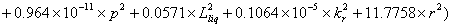 (14)
(14)
In the safety computations, the safety-index is found to be 1.916 (13.2% less than b-MCS) while the probability of failure equals 2.77×10-2. The most important variables are found to be; soil pressure (p); the thickness of the liquefied layer (LLiq); the rotational stiffness (kr) and the pile diameter (r), with relative importance; 84.3%; 34%; 30.5% and 21.1%; respectively. It is obvious that the sensitivities of response surface method are very close to that of the actual explicit limit state using SORM, (Case 2 in Table 4.)
Table 3. Statistical Characteristic of Random Variables - Example 2.
| | Random variables | Sym. | Dist. | Nominal | Mean | COV | Ref. |
| 1 | Lateral pressure | p | EV-I | 10.5 kN/m2 | 10.5 | 0.25* | * |
| 2 | Radius | r | LN | 0.30 m | 0.30 | 0.10 | [14] |
| 3 | Thickness | t | LN | 3.4 cm | 3.4 | 0.05 | [14] |
| 4 | Length | LLiq | N | 6.00 m | 6.00 | 0.04* | * |
| 5 | Pile E-modulus | E | LN | 3300 MPa | 3300 | 0.06* | * |
| 6 | Rotational spring | kr | LN | 5738 kN m/rad | 5738 | 0.21* | * |
* Data not available. Assumed parameters are based on engineering judgment.
Table 4. Results of Reliability Analysis - Example 2.
| | | Variables sensitivities | β | Pf | No. of calls |
| | | p | LLiq | kr | r | E | t | | | |
| | i) Explicit limit state | | | | | | | | | |
| 1 | Monte Carlo* | | | | | | | 2.209 | 1.36×10-2 | 105 |
| 2 | SORM | -0.838 | -0.398 | 0.283 | 0.213 | -0.093 | 0.064 | 2.213 | 1.35×10-2 | 1 |
| | ii) Response surface | | | | | | | | | |
| 3 | Preliminary analysis | -0.946 | -0.245 | 0.163 | 0.116 | 0.054 | 0.037 | 2.602 | 4.64×10-3 | 13 |
| 4 | Quadratic response | -0.843 | -0.340 | 0.305 | 0.211 | ----- | ----- | 1.916 | 2.77×10-2 | 9 |
7.3. Example 3: Limit Equilibrium Finite Element Model (LEFE)
Herein, example 2 is resolved but using the LE-based finite element method. As mentioned above, in the LE-based FE model, the soil is represented by 8-node solid Drucker Prager element while the pile is modeled by 3-D beam element, as shown in Figure 1-c. By this presentation, the soil nonlinearity as well as more other variables is taken into account. Table 5, shows the statistical properties of the system-related variables (11 variables). These properties are gathered from the literature [12-14].
7.3.1. Monte Carlo Simulation
The flexural strength of the pile is assumed the same as the reinforced concrete, fc = 2250 kN/m2. The limit state can be obtained by substituting Eq. 1 in Eq. 9:
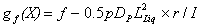 (15)
(15)
7.3.2. Response Surface Integrated with LEFE Model
The analysis is started by setting up the FE model. The moment of the model is 112.1 k.Nm, which is in good agreement with the moment of the centrifuge model, 113 k.Nm, as in [7]. As the model moment is approximately the same moment value of the test, no model correction is used.
As in the above example, a preliminary analysis is performed using the first order polynomial. Hence, the variables of low sensitivities are excluded from the formulation. This large number of variables is reduced to only 4 variables; the soil pressure (p), the pile radius, (r), the thickness of the liquefied layer (LLiq) and the pile thickness (t) with sensitivities; 0.78; 0.41; 0.18 and 0.12; respectively.
Following the same procedure as in the above example, the reliability analysis is preformed using the quadratic polynomial. The response surface function is derived as follow:
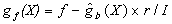
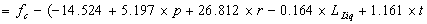
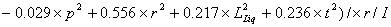 (16)
(16)
Table 5. Statistical Characteristic of Random Variables - Example 3.
| | | Random variables | Sym. | Dist. | Nominal | Mean | Bias | COV | Ref. |
| 1 | Load | Lateral pressure | p | EV-I | 10.5 kN/m2 | 10.5 | 1.0 | 0.25* | |
| 2 | Pile | Pile E-modulus | E | LN | 3.3×106 kN/m2 | 3300 | 1.0 | 0.06* | |
| 3 | | Poisson’s ratio | vc | LN | 0.2 | 0.2 | 1.0 | 0.10 | * |
| 4 | | Concrete density | γC | N | 25 kN/m3 | 25 | 1.0 | 0.10 | [12] |
| 5 | | Radius | r | LN | 0.30 m | 0.30 | 1.0 | 0.10 | [14] |
| 6 | | Thickness | t | LN | 3.4 cm | 3.4 | 1.0 | 0.05 | [14] |
| 7 | | Length | LLiq | N | 6.00 m | 6.00 | 1.0 | 0.04* | * |
| 8 | Soil layer | Soil E-modulus | E | LN | 1500 kN/m2 | 1725 | 1.15 | 0.21* | [13] |
| 9 | | Friction angle | φ | LN | 35º | 36.05 | 1.03 | 0.20 | [13] |
| 10 | | Poisson’s ratio | vs | LN | 0.4 | 0.4 | 1.0 | 0.10 | [13] |
| 11 | | Soil density | γs | LN | 17 kN/m2 | 17 | 1.0 | 0.10 | [13] |
| 12 | | Flexural strength | fc | LN | 2250 kN/m2 | 2250 | 1.0 | 0.18* | [12] |
* Data not available. Assumed parameters are based on engineering judgment
Table 6. Results of Reliability Analysis- Example 3.
| | | Variables sensitivities | β | Pf | No. of calls |
| | | fc | p | r | LLiq | t |
| | i) Explicit limit state | | | | | | | | |
| 1 | Monte Carlo* | | | | | | 1.522 | 6.40×10-2 | 105 |
| 2 | SORM | 0.436 | -0.789 | 0.345 | -0.231 | 0.120 | 1.506 | 6.60×10-2 | 1 |
| | ii) Response surface | | | | | | | | |
| 3 | First order polynomial | 0.423 | -0.781 | 0.405 | -0.184 | 0.116 | 1.455 | 7.29×10-2 | 25 |
| 4 | Quadratic polynomial | 0.450 | -0.780 | 0.334 | -0.250 | 0.123 | 1.482 | 6.91×10-2 | 9 |
The most important variables are listed in Table 6. They are; fc; p; r; LLiq and t, with sensitivities; 0.45; -0.780; 0.334; -0.250 and 0.123, respectively.
8. Discussion
In example 1 and example 2, it is obvious that the response surface method yields results in good agreement with that of actual explicit limit state function. While in example 3, more variables are incorporated in the LE-based finite element model. In other words, more uncertainties can be taken into account. Coupling the LEM with the response surface method enables the analyst to predict the failure. In short time, the failure information can be predicated and evaluated. Both the drift and strength safety can be investigated.
The suggested method is an approximate method as it is based on the simplified LEM. The LEM can take the effect of pile cap and the effect of the densified sand around the pile into consideration. In the LE-based FE-model, the flexibility of the bottom non-liquefiable layer is more realistic represented using 3D beam element for the pile and Drucker-Prager model for the non-liquefied layer.
On the other hand, the method does not take the interaction with adjacent piles into account. Many soil parameters are not included in the formulation to simplify the problem. Moreover, there is an endless number of other soil profiles and pile head constraints that may be encountered in practice, but could not be included to this study.
9. Conclusion
In the literature, the risk of pile failure subjected to lateral spread can be predicted by conducting the typical beam-spring model with the Monte Carlo Simulation. As another alternative method, the paper introduces a quick method to predict pile failure induced by lateral spread. In the proposed methodology, the Finite element method (FEM), is used to build up a LE-based finite element model. This model is coupled with (SORM) via the response surface method (RSM). The finite element model represents the soil by 3D solid elastoplastic (Drucker-Prager failure criterion) while the pile is represented by elastic 3D beam element. The method is validated using Monte Carlo Simulation. Both operational and structural limit states are used. For the considered example, the soil pressure and the radius of pile are found to be the most sensitive variables.
Nomenclature
| b0, bi, bii, and bij | Unknown coefficients of a polynomial to be determined. |
| c | The soil cohesion strength. |
| Dp | The diameter of pile. |
| E, Es | The young's modulus of pile material and soil, respectively. |
| EI | The flexural rigidity of the pile. |
| FORM | First order reliability methods. |
| f, fc | The flexural strength of the pile material and reinforced concrete, respectively. |
| 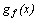 , ,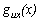
| Explicit expression of flexural and drift limit state function, respectively |
| g(X) | Limit state function. |
| 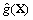
| Response surface function. |
| 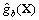 , , 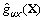
| The response surface function of bending moment and drift, respectively. |
| 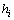
| A chosen factor that defines the experimental/sample region. |
| Lliq | The thickness of the liquefiable soil layer |
| I | Second moment of inertia of the pile. |
| k | The number of random variables in the formulation. |
| kr | The rotational stiffness of the pile base. |
| Lliq | the thickness of the liquefiable soil layer |
| M | The bending moment. |
| MCS | Monte Carlo Simulation. |
| p | Soil pressure. |
| pₒ | The numbers of coefficients necessary to define a polynomial. |
| Pf | The probability of failure. |
| r | The pile radius. |
| RSM | Response surface method. |
| SORM | Second order reliability method. |
| t | The pile thickness. |
| ux | The pile head displacement. |
| Xall | The allowable drift. |
| 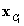 , , 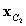
| First and second center point. |
| 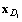
| The coordinates of the design point. |
| Xi (i = 1, 2,¼, k) | The ith random variable |
| 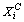
| The coordinates of the centre point, i. |
| b | b-index =Reliability index. |
| ε | Pre-selected convergence criterion |
| 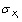
| The standard deviation of a random variable Xi. |
| v, vs | Concrete and soil Poisson’s ratio, respectively. |
| γ, γs | Unit density of reinforced concrete and soil, respectively. |
| φ | The angle of internal friction. |
References
- Bradley, B., Cubrinovski, M., Dhakal, R., and MacRae, G., Probabilistic seismic performance and loss assessment of a bridge–foundation–soilsystem. Soil Dynamics and Earthquake Engineering2009.
- Cubrinovski, M., Uzuoka, R., Sugita, H., Tokimatsu, K., Sato, M., and Ishihara, K., Prediction of pile response to lateral spreading by 3-Dsoil-water coupled dynamic analysis: shakingin the direction of ground flow. Soil Dynamics and Earthquake Engineering, 2008.
- Valsamis, A., Bouckovalas, G., and Papadimitriou, A., Parametric investigation of lateral spreading of gently sloping liquefied ground. Soil Dynamics and Earthquake Engineering, 2010. 30(6): p. 490–508.
- Andrianopoulos, K., Papadimitriou, A., and Bouckovalas, G., Explicit integration of bounding surface model for the analysis of earthquake soil liquefaction. Journal for Numerical and Analytical Methods in Geomechanics, 2010.
- Andrianopoulos, K., Papadimitriou, A., and Bouckovalas, G., Bounding surface plasticity model for the seismic liquefaction analysis of geostructures. Soil Dynamics and Earthquake Engineering, 2010.
- Valsamis, A.I., Bouckovalas, G.D., and Chaloulos, Y.K., Parametric analysis of single pile response in laterally spreading ground. Soil Dynamics and Earthquake Engineering, 2012. 34(1): p. 99-110.
- Dobry, R., Abdoun, T., O’Rourke, T., and Goh, S., Single Piles in Lateral Spreads: Field Bending Moment Evaluation. Journal of Geotechnical and Geoenvironmental Engineering, 2003. 129(10): p. 879-889.
- Bradley, B., Cubrinovski, M., and Haskell, J., Probabilistic pseudo-static analysis of pile foundations in liquefiable soils. Soil Dynamics and Earthquake Engineering, 2011. 31(10): p. 1414-1425.
- Farag, R., Limit Equilibrium Safety Analysis of Pile In Lateral Spread: Three-Layer, in International Conference on Advances in Structural and Geotechnical Engineering, ICASGE’15, 2015: Hurghada, Egypt.
- Structural Research and Analysis Corporation (SRAC), COSMOSM. V. 2.6: FE Program. 2000.
- Haldar, A. and Mahadevan, S., Probability, Reliability and Statistical Methods in Engineering Design. 1st ed. 2000a, New York: John Wiley & Sons.
- National Bureau of Standard (NBS), Development of a Probability Based Load Criterion for American National Standard A58: Building Code Requirements for Minimum Design Loads in Buildings and Other Structures., in special publication 5771980, U.S. Department of Commerce,.
- Joint Committe on Structural Safety (JCSS), Probabilistic Model Code: Soil properties, 2006, Available from: www.jcss.ethz.ch., http://www.jcss.byg.dtu.dk/.
- Bednar, H., Pressure Vessel Design Handbook. 1986, Malabar, Florida: Van Nostrand Reinhold.