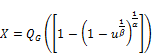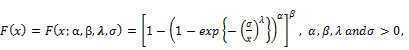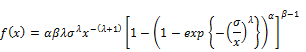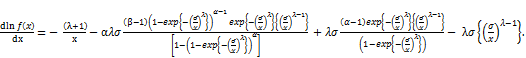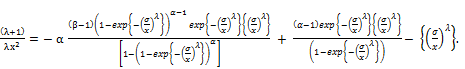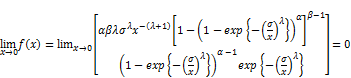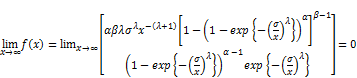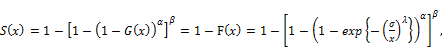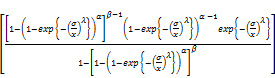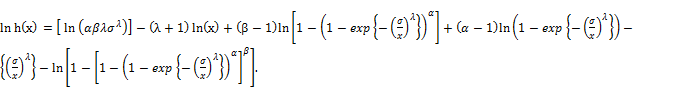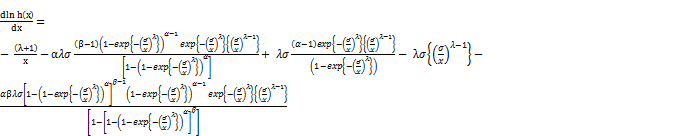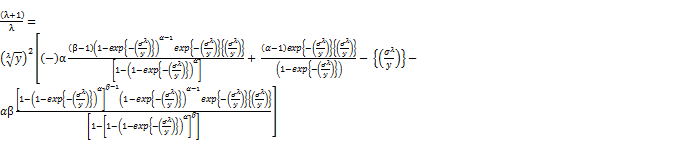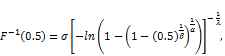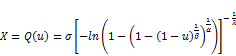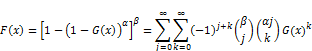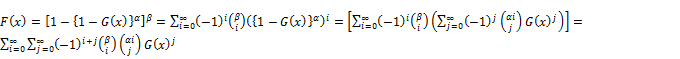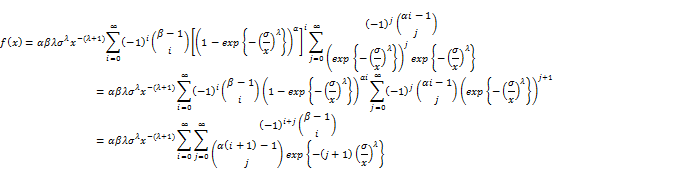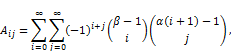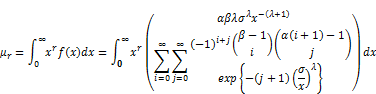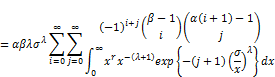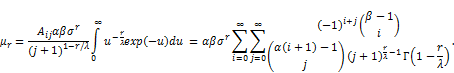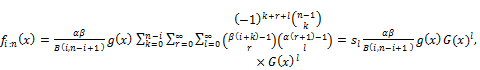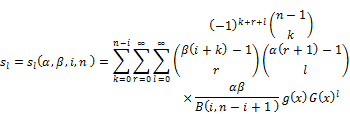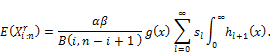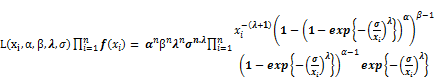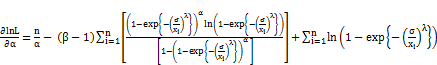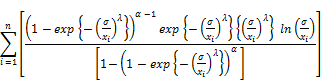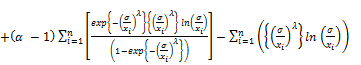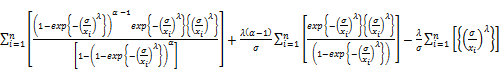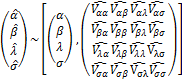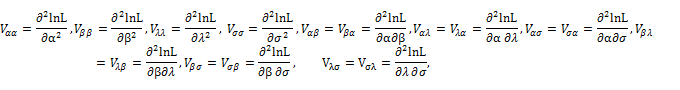Exponentiated Generalized Fréchet Distribution
Abd-Elfattah A. M.1, Assar S. M.2, Abd-Elghaffar H. I.3, *
Institute of Statistical Studies & Research, Department of Mathematical Statistics, Cairo University, Cairo, Egypt
Email address

(Abd-Elfattah A. M.)

(Assar S. M.)
hanaaibrahim.2013@gmail.com (Abd-Elghaffar H. I.)
*Corresponding author
Citation
Abd-Elfattah A. M., Assar S. M., Abd-Elghaffar H. I. Exponentiated Generalized Fréchet Distribution. International Journal of Mathematical Analysis and Applications. Vol. 3, No. 5, 2016, pp. 39-48.
Abstract
Recently Cordeiro et al. [1] proposed a new class ofdistributions that extends exponentiated type distributions, named as exponentiated generalized class of distributions. Many special models are obtained from this class; one of them is exponentiated generalized Fréchet distribution. In this paper, some properties of the exponentiated generalized Fréchetdistribution will be discussed, including the shape of the probability density function, hazard rate function, and quantile function. The moment, the moment generating function and order statistics are obtained. Finally, the statistical properties of the model are provided and the method of maximum likelihood estimation was proposed in estimating its parameters.
Keywords
Exponentiated Generalized Fréchet Distribution, Hazard Function, Quantile Function, Moments, Order Statistics, Maximum Likelihood Method
1. Introduction
Statisticaldistributions are very useful in describing and predicting real data analysis. Although many distributions have been developed, there are always techniques for developing distributions which are either more flexible or for fitting specific real data analysis. In recent years, some different generalizations of continuous distributions have received great attention in the literature.Broadly speaking, there has been an increased interest in defining new generators for univariate continuous families of distributions by introducing one or more additional shape parameter(s) to a baseline distribution. The Exponentiateddistributionshave been studied widely in statistics since 1995 and a number of authors have developed various classes of these distributions. One of thesegenerators is the exponentiated generalized (EG) class of distributions pioneered by Cordeiro et al. [1]. For an arbitrary baseline cumulative distribution function (cdf) G(x), they defined the probability density function (pdf) f(x) and the cdf F(x) by
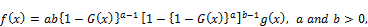 (1)
(1)
and
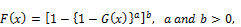 (2)
(2)
respectively, where 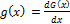 and a, b are two extra shape parameters to those of the G distribution. A new method of adding two parameters to a continuous distribution that extends the idea first introduced by Lehman [2] and exponentiated distributions have been studied by several authors, the exponentiated Fréchet (EF) distribution is a special case of general class of exponentiated distribution proposed by Gupta et al. [3]; Nadarajah and Kotz [4] studied some of the mathematical properties of the standard Fréchet distribution and the cdf is given by
and a, b are two extra shape parameters to those of the G distribution. A new method of adding two parameters to a continuous distribution that extends the idea first introduced by Lehman [2] and exponentiated distributions have been studied by several authors, the exponentiated Fréchet (EF) distribution is a special case of general class of exponentiated distribution proposed by Gupta et al. [3]; Nadarajah and Kotz [4] studied some of the mathematical properties of the standard Fréchet distribution and the cdf is given by
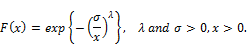
They introduced the exponentiated exponential (EE) distribution as a generalization of standard exponential distribution. The exponentiated exponential (EE) distribution is defined by cumulative distribution function (cdf) 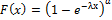 , where x, λ, α
, where x, λ, α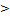 0, and α-th is a power of standard exponential cumulative distribution.They defined the cdf of the new distribution called generalized Fréchet (GF) distribution and defined the form by:
0, and α-th is a power of standard exponential cumulative distribution.They defined the cdf of the new distribution called generalized Fréchet (GF) distribution and defined the form by:
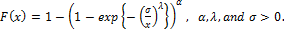 and the pdf
and the pdf
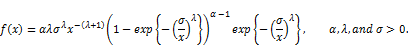
In this model, 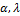 are shape parameters and
are shape parameters and 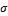 is a scale parameter.
is a scale parameter.
Abd-Elfattah et al.[5] extended this work and written the families of exponentiated distributions which given by 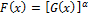 , where
, where  is the distribution function of a corresponding non-generalized distribution and
is the distribution function of a corresponding non-generalized distribution and 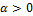 denotes the generalized parameter.They estimated unknown parameters by maximum likelihood (ML) method and used in Fisher information matrix for GF models, they application for queues in supermarkets, sea currents, wind speeds and track race records, Abd-Elfattah et al. [6] proposed goodness of fit test for generalized Fréchet distribution.
denotes the generalized parameter.They estimated unknown parameters by maximum likelihood (ML) method and used in Fisher information matrix for GF models, they application for queues in supermarkets, sea currents, wind speeds and track race records, Abd-Elfattah et al. [6] proposed goodness of fit test for generalized Fréchet distribution.
Silva et al. [7] studied some of its structural properties and the exponentiated Fréchet model, but they adopt the EF terminology since
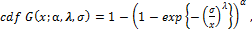 is not in the typical exponentiated form and the pdf is given by:
is not in the typical exponentiated form and the pdf is given by:
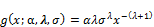
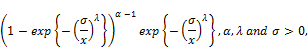
and extended this distribution proposed by called exponentiated generalized (EG) class of distribution.
Cordeiro et al. [1] obtained a new method for adding two parameters to a continuous distribution that extends the first idea of exponentiated type distribution, and they obtained some of its structural. The cdf and pdf are given by:
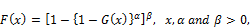 (3)
(3)
and
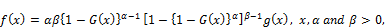 (4)
(4)
where α and β are two additional shape parametersand 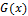 is the standard cumulative distribution function. In this Equation (4) there is no complicated in contrast with the beta generalization family (Eugene et al. [8]), which also includes two extra parameters but involves the beta incomplete function. We can use the special form for simulations sinceits quantile function takes a simple form, called
is the standard cumulative distribution function. In this Equation (4) there is no complicated in contrast with the beta generalization family (Eugene et al. [8]), which also includes two extra parameters but involves the beta incomplete function. We can use the special form for simulations sinceits quantile function takes a simple form, called
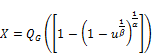 ,
,
where QG(u) is the baseline quantile function. 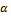 and
and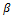 are two additional shape parameters,
are two additional shape parameters,
The EG family of densities f(x) allows for greater flexibility of its tails and canbe widely applied in many areas of engineering and biology. If 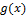 is a symmetric distribution, the distribution
is a symmetric distribution, the distribution  will not be a symmetric distribution. The two extra parameters in Equation (4) can control both tail weights and possibly add entropy to the center of the EG density function.
will not be a symmetric distribution. The two extra parameters in Equation (4) can control both tail weights and possibly add entropy to the center of the EG density function.
For short the exponentiated-G (Exp-G) distribution an alternative for parent distribution 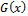 and called Lehmann type I distribution Expc(G).
and called Lehmann type I distribution Expc(G).
Cordeiro et al. [1] said X ~ ExpcG, if X has a cumulative function as defined by 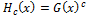 and density functions as defined by
and density functions as defined by 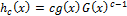 for c > 1 and c < 1 and for larger values of x, the multiplicative factor
for c > 1 and c < 1 and for larger values of x, the multiplicative factor 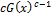 is greater and smaller than one, respectively. The reverse assertion is also true for smaller values of x. We can imply that the ordinary moments associated with the density function
is greater and smaller than one, respectively. The reverse assertion is also true for smaller values of x. We can imply that the ordinary moments associated with the density function 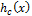 are strictly larger (smaller) than those associated with the density
are strictly larger (smaller) than those associated with the density 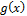 when c > 1 and c < 1.There is a dual transformation
when c > 1 and c < 1.There is a dual transformation 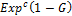 , referred to as the Lehmann type II distribution corresponding to the cdf
, referred to as the Lehmann type II distribution corresponding to the cdf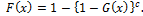
If α = 1, the Lehmann type I take the form 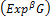 distributions.
distributions.
If β = 1, the Lehmann type II take the form  distributions.
distributions.
If α and β are positive integers the double transformation takes the form 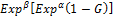 generates the EG class of distributions and deviate of several properties of the EG class by this double transformation.The class of EG distributions shares an attractive physical interpretation whenever α and β are positive integers.
generates the EG class of distributions and deviate of several properties of the EG class by this double transformation.The class of EG distributions shares an attractive physical interpretation whenever α and β are positive integers.
Let Xj1,…, Xjα denote the lifetimes of the subcomponents within the jth component, j = 1,…, β; with common cdf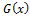 .
.
Let Xj denote the lifetime of the jth component and let X denote the lifetime of the device. We consider a device made of β independent component in a parallel system and each component is made of α independent subcomponents identically distributed according to 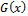 in a series system. The device fails if all β components fail and each component fails if any subcomponent fails.Then, the CDF of X is:
in a series system. The device fails if all β components fail and each component fails if any subcomponent fails.Then, the CDF of X is:
P(X ≤ x) = P(X1 ≤ x,…, Xβ ≤ x) = P(X1 ≤ x)β= [1 - P(X1> x)]β
= [1 - P(X11> x,…, X1α> x)]β = [1 - P(X11> x)α]β
=[1-{1-P(X11≤x)}α]β.
So, the lifetime of the device dependent on the EG family of distributions.
Many authors extended the special cases for exponentiated generalized class of distributions and studied some of the mathematical properties.
The rest of the paper is organized as follows. In Section 2, we define the EGF distribution and shapes of the density function, explicit expressions for cumulative and density function. Asymptotic behavior, hazard rate function in Section 3. Also, some important statistical properties of the exponentiated generalized Fréchet distribution (EGF) such as the quantile function, expansions for the density function were discussed and we derive closed form expressions for the moment, moment generating function and order statistics of the EGF distribution in Section 4. Finally the maximum likelihood estimates (MLEs) of the four parameters are given Section 5.
2. Some Properties of Special Model for Exponentiated Generalized Class Distributions
In this section, we present special models of the EG class corresponding to the Fréchet distribution.
2.1. Exponentiated Generalized Fréchet Distribution
The EGF distribution was proposed by Codeiro et al. [1], but they did not study its mathematical properties.The cumulative distribution function cdf of baseline 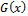 , and probability density function pdf of
, and probability density function pdf of 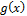 , of the EGF distribution given by:
, of the EGF distribution given by:
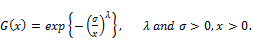 (5)
(5)
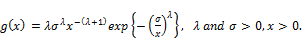 (6)
(6)
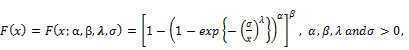 (7)
(7)
and
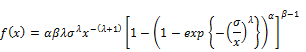
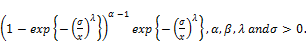 (8)
(8)
In this model, 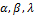 are shape parameters and
are shape parameters and 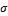 is a scale parameter. Where
is a scale parameter. Where 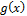 is symmetric distribution, the resulting model in Equation (8) will not be a symmetric model because the two parameters
is symmetric distribution, the resulting model in Equation (8) will not be a symmetric model because the two parameters 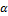 and
and 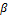 can control the tail weights and possibly add entropy to the center of the exponentiated generalized family of distribution.
can control the tail weights and possibly add entropy to the center of the exponentiated generalized family of distribution.
(See, Cordeiro et al. [1]).
Note, a random variable X having density function (8) is denoted by X~ EGF (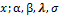 ) in order to eliminate the dependence on the model parameters.The standard Fréchet distributionin Equation (5) is cleary a special case of (7) when
) in order to eliminate the dependence on the model parameters.The standard Fréchet distributionin Equation (5) is cleary a special case of (7) when 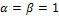 . Setting,
. Setting, 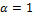 given the exponentiated type distributions defined by Gupta et al. [3], and we can be obtained exponentiated generalized Fréchet (EGF) distributions and exponentiated generalized Gumbel (EGu) if
given the exponentiated type distributions defined by Gupta et al. [3], and we can be obtained exponentiated generalized Fréchet (EGF) distributions and exponentiated generalized Gumbel (EGu) if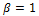 as defined by Cordeiro et al. [1] and Andrade et al. [9] respectively.
as defined by Cordeiro et al. [1] and Andrade et al. [9] respectively.
2.2. Shape of the Probability Density Functions
The first derivative of ln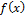 for the exponentiated generalized Fréchet distribution is obtaind as followes:
for the exponentiated generalized Fréchet distribution is obtaind as followes:
 (9)
(9)
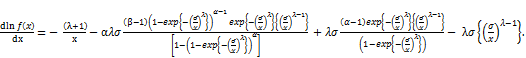 (10)
(10)
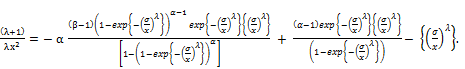 (11)
(11)
Standard calculations based on this derivative show that f(x) exhibits a single mode at x = x0 is a root of (11) with 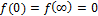 , where x0 is the solution of dln f(x)/dx=0, the critical values of f(x) are a root of (11), then we can classify it as local maximum, local minimum or inflection point we have,
, where x0 is the solution of dln f(x)/dx=0, the critical values of f(x) are a root of (11), then we can classify it as local maximum, local minimum or inflection point we have,  where
where  (See, Nadarajah & Kotz [10]).
(See, Nadarajah & Kotz [10]).
Figures 1 and 2 illustrate plots for the pdf and cdf of EGF distribution for selected values of the parameters.
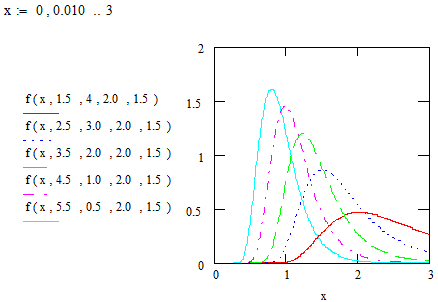
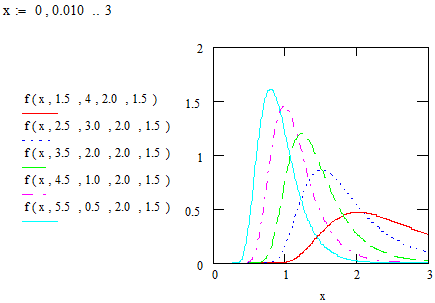
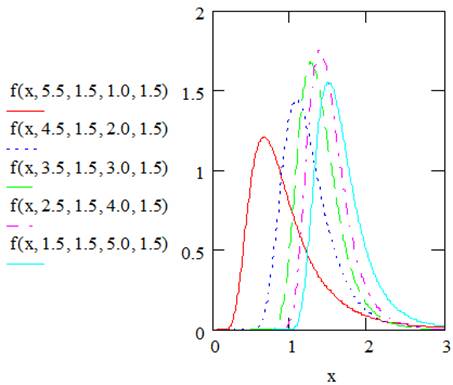
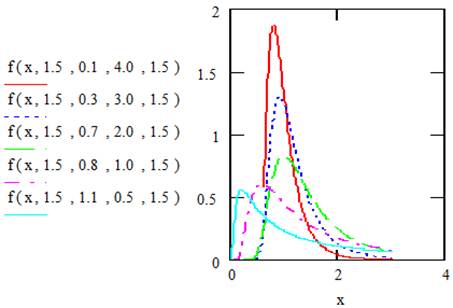
Figure 1. Plots of the probability density functionof EGF distribution.
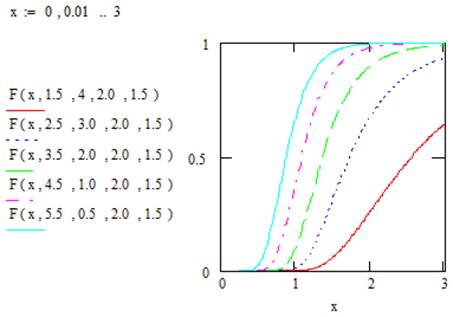
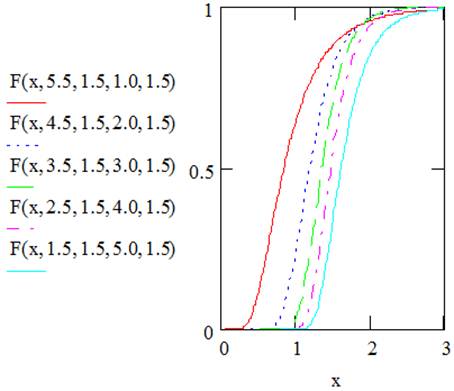
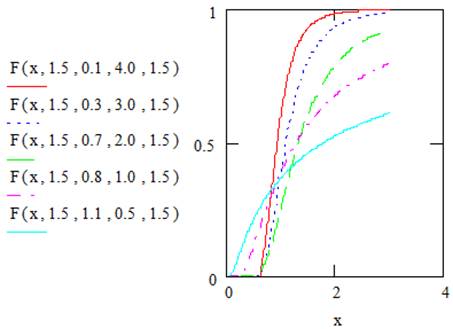
Figure 2. Plots of the cumulative function of the EGF distribution.
3. Properties of the Proposed Model
In this section, we present the structural properties of the EGF distribution
3.1. Asymptotic Behavior
we can obtain the investigation of the behavior of proposed model as given in Equation (8) as 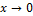 and
and 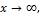 and taking limiting for
and taking limiting for 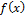
where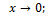
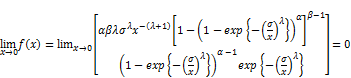 (12)
(12)
And 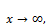
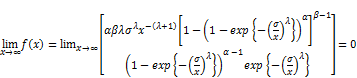 (13)
(13)
These results confirm further that the proposed distribution has a mode.
(See, Oguntunde et al. [11]).
3.2.Hazard Rate Function
The survival and hazard rate function of the (EGF) distributions are defined by:
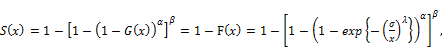 (14)
(14)
and the hazard rate function of EGF is given by:
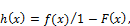 (15)
(15)
is an important quantity characterizing life phenomena for the EGF distribution, h(x) take the form
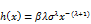
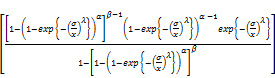 (16)
(16)
we can calculate the first derivative of ln h(x) with respect to x as follows:
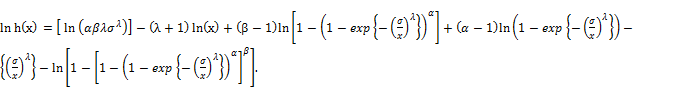 (17)
(17)
Then
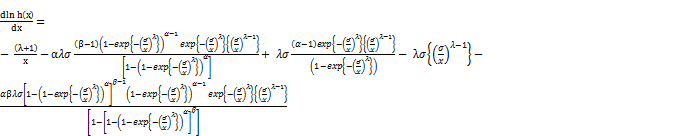 (18)
(18)
Then
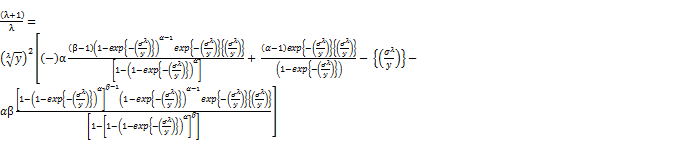 (19)
(19)
Standard calculations based on this derivative show that h(x) exhibits a single mode at x = x0 with h(0) = h( ) = 0, where y0 =
) = 0, where y0 =  is the solution of (19) respectively.
is the solution of (19) respectively.
(See, Nadarajah & Kotz [10]).
Figures 3 and 4 illustrate plots of survival and hazard rate functions of EGF distribution for selected values of the parameters.
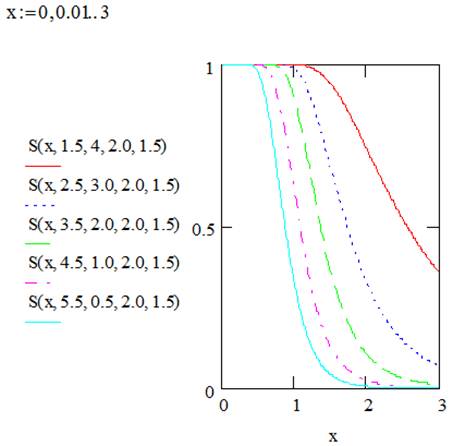
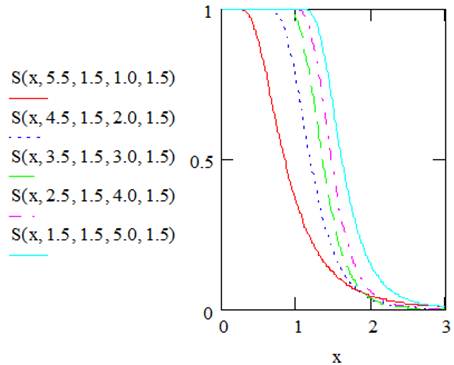
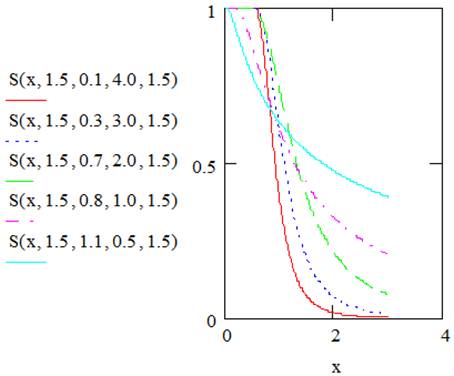
Figure 3. Shows plots of survival functions of EGFdistribution.
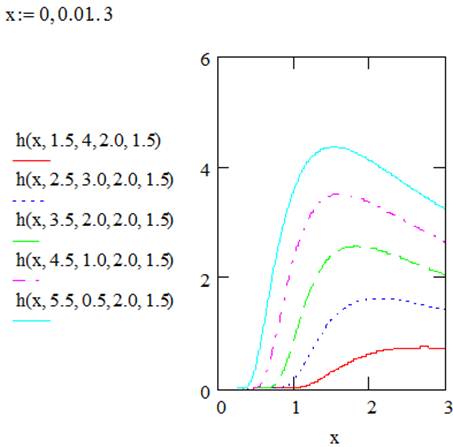
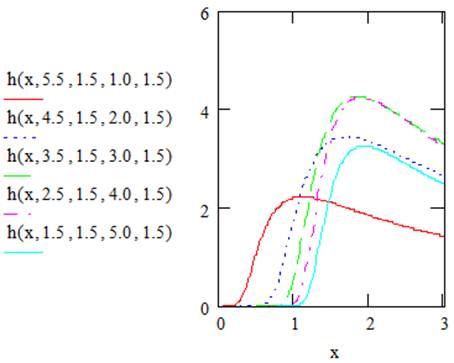
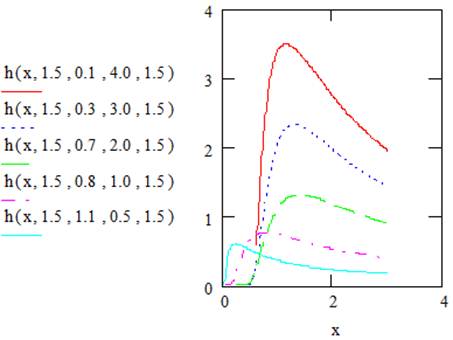
Figure 4. Shows plots of the hazard rate functions of the EGFdistribution.
4. Some Properties of Exponentiated Generalized Fréchet Distribution
In this section, we study some statistical properties of EGF distribution, specifically quantile function, expansions for the density function and order statistics.
4.1. Quantile Function
The quantile function and median are given by:
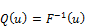
Therefore, the corresponding quantile function for the proposed model is given by:
 (20)
(20)
Let U has the uniform U(0, 1) distribution. we obtain the median by substituting u=0.5. here the median of the proposed model is given by:
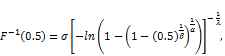 (21)
(21)
(See, Oguntunde et al.[11], and Elbatal and Hiba [12]), to simulate the EGF distribution is a quite strength forward using the means of inverse transformation method, we consider the random variable x given by:
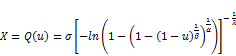 , (22)
, (22)
the effect of the additional shape parameter 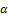 , and
, and  for stander Fréchet distribution on skewness and kurtosis of a new distribution based on quantile measure.
for stander Fréchet distribution on skewness and kurtosis of a new distribution based on quantile measure.
4.2. Expansions for Cumulative Distribution and the Density Function
The power series expansion for real non-integer β given by:
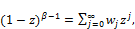 (23)
(23)
where
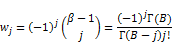
Which is valid for 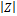 < 1. Replace (23) by (3) and using the binomial expansion for a positive real power
< 1. Replace (23) by (3) and using the binomial expansion for a positive real power
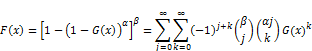
Then
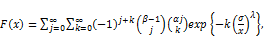 (24)
(24)
and
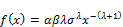
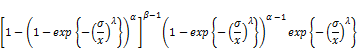
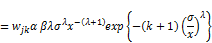
where
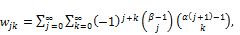 (25)
(25)
(See, Cordeiro et al. [1]).
4.3. Moments
In this section, we discuss the general formulae for the r th moment for EGF distribution is given by:
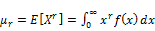 (26)
(26)
general formulae for the moments where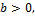 and real noninteger, we have the infinite power series
and real noninteger, we have the infinite power series
 (27)
(27)
where the binomial coefficient is defined for any real b, 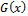 is EGF distribution if b is an integer, the index i in previous sum stop at b-1 from Equation (1) and from Equation (3) the cdf is:
is EGF distribution if b is an integer, the index i in previous sum stop at b-1 from Equation (1) and from Equation (3) the cdf is:
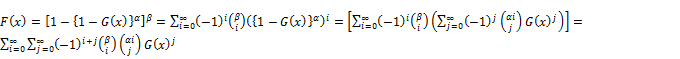 (28)
(28)
from Equations (5) and (7)we have a cumulative function
 (29)
(29)
and from Equation we have a probability density function(8)
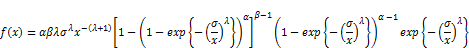
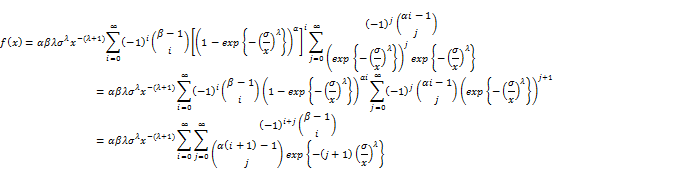
Then
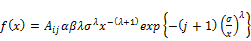 (30)
(30)
where
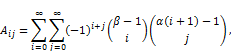
from Equation (26) and (30), we can obtain
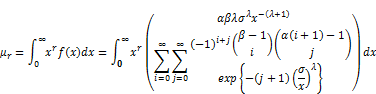
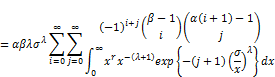
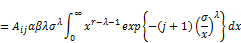
Setting 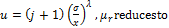
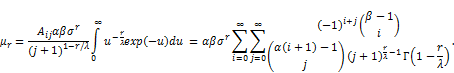
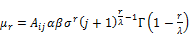 (31)
(31)
4.4. Moment Generating Function
In this section, we derive the moment generating functionofEGF distribution. Let 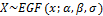 distribution then moment generating function (mgf)
distribution then moment generating function (mgf) 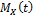 is given by:
is given by:
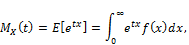
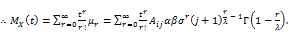 (32)
(32)
since 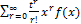 the integral converges for all t close to 0 the mgf
the integral converges for all t close to 0 the mgf 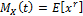 by replacing
by replacing  the Equation (31) the result is obtained Equation (32).
the Equation (31) the result is obtained Equation (32).
(See, Cordeiro et al. [1], Elbatal and Hiba [12]).
4.5. Order Statistics
In this section, we derive closed form expressions for the pdfsof theith order statistic of the EGF distribution;
Let Y1,…,Yn random variables from iid, i=1,…,n.
The density 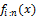 of the ith order statistic is given by
of the ith order statistic is given by
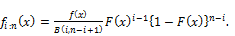 (33)
(33)
where 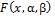 and
and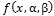 are the cdf and pdf of the EG Class distribution given by (3) and (4) respectively, and
are the cdf and pdf of the EG Class distribution given by (3) and (4) respectively, and 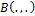 is the beta function. Substituting equation (3) and (4) and we can be written
is the beta function. Substituting equation (3) and (4) and we can be written
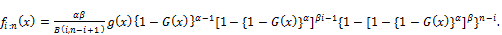 (34)
(34)
The binomial series expansion, 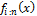 can be used and written by
can be used and written by
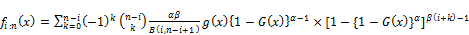 (35)
(35)
we can be replaced equation (23) where  real non integer to the last term and we can obtain
real non integer to the last term and we can obtain
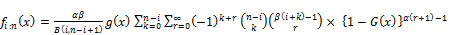 (36)
(36)
This Equation can be rewritten as
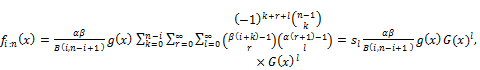 (37)
(37)
Where the coefficients 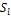 can be calculated as
can be calculated as
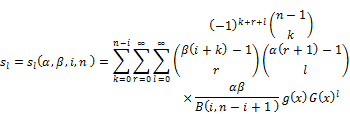
We can be rewritten the Equation (37) of the Exp-G density functions as
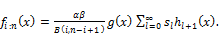 (38)
(38)
The Equation (38) is the main result because, the density function of the EGF order statistic is a linear combination of Exp-G densities.We canobtain several mathematical properties such as incomplete moments, generating functionand mean deviations.The ithordinary moment of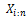 isdefined by
isdefined by
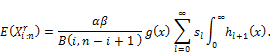
(See, Cordeiro et al. [1], and Elbatal and Hiba [12]).
5. Maximum Likelihood Estimators (ML)
In this section, the problem of estimation of the unknown four parameters for the special models of the exponentiated generalized (EG) class distributions will be discussed.
The maximum likelihood estimates (MLEs) of theparameters of the EG distribution from complete samples.
LetX1,…,Xn be a random sample of size n from an exponentiated generalized Fréchet distribution with unknown parameters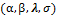 , the likelihood function takes the form
, the likelihood function takes the form
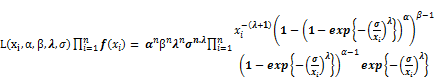 (39)
(39)
Then the log-likelihood function 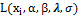 can be written as
can be written as
 (40)
(40)
The normal equations become
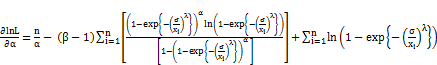 (41)
(41)
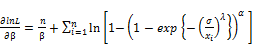 (42)
(42)
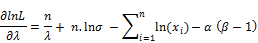
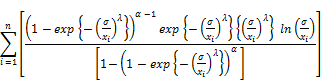
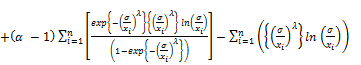 (43)
(43)
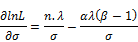
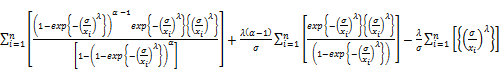 (44)
(44)
The MLE of can be obtained by solving theEquations (41), (42), (43) and (44) using
can be obtained by solving theEquations (41), (42), (43) and (44) using
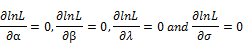
we can't be solved analytically and require statistical software with iterative numerical techniques.
we can use software package Math Cad (2001) to solve a nonlinear equation.
Also, we obtain the 4 4 observed information matrix through,
4 observed information matrix through, 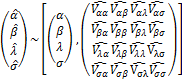
The inverse of the matrix results in the well-known variance-covariance matrix. we can calculate the observed information since its expectation requires numerical integration. The 4×4 observed information matrix is approximate Fisher information matrix 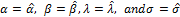

where
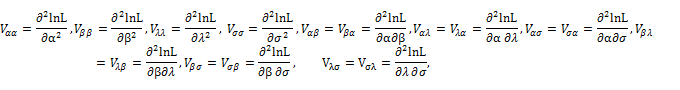
By solving this inverse dispersion matrix these solution will yield asymptotic variance and covariance's of these ML estimators for 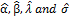 .We approximate
.We approximate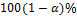 confidence intervals for
confidence intervals for 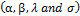 are determined respectively as
are determined respectively as 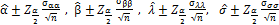 . where
. where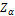 is the upper 100
is the upper 100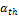 the percentile of the standard normal distribution.
the percentile of the standard normal distribution.
(See, AbdElfattah and Omima [5], Oguntunde et al. [11] and Elbatal and Hiba ([12]).
6. Conclusions
In this paper, we study a new four-parameter for the exponentiated generalized Fréchet (EGF) distribution. This model generalizes the Fréchet distribution, which is one of the most important models for fitting data with support and using Math Cad (2001). We provide some mathematical properties of the EGF distribution including ordinary moment, moment generating and quantile functions.
The density function of the order statistics is obtained as a mixture of exponentiated Fréchet densities. We discuss the parameter estimation by maximum likelihood and provide the observed information matrix. We provide a Monte Carlo simulation study to evaluate the maximum likelihood estimation of the model parameters. Further, using a goodness of fit test based on correlation coefficient test.
References
- Cordeiro, G. M., Ortega E. M. and Cunha D. C. (2013). The Exponentiated Generalized Class of Distributions, "Journal of Data Science", 11: 1-27.
- Lehmann, E. L. (1953). The power of rank tests. Annals of Mathematical Statistics 24(1):23-43.
- Gupta, R. C., Gupta P. L., and Gupta R. D., (1998) Modeling failure time data by Lehman alternatives. "Communications in Statistics, Theory and Methods", 27:887–904.
- Nadarajah S., and Kotz S. (2006). The exponentiated type distributions. "ActaApplicandaeMathematicae", 92(2): 97-111.
- Abd-Elfattah A. M., Omima A. M. (2009). Estimation of Unknown Parameters of Generalized Fréchetdistribution,"Journal of Applied SciencesResearch", 5(10):1398-1408.
- Abd-Elfattah A. M., Fergany H. A., Omima A. M. (2010). Goodness-Of- Fit Test for the Generalized Fréchet distribution," Australian Journal of Basic and Science", 4(2):286-301.
- Silva R. V., Andrade T. A. N., Maciel D. B. M., Campos R. P. S., and Cordeiro G. M. (2013) A new lifetime model: The Gamma extended Fréchet distribution." Journal of Statistical Theory and Applications", 12(1): 39-54.
- Eugene N., Lee C. and Famoye F. (2002). Beta-normal distribution and its applications. "Communications in Statistics - Theory and Methods", 31(4):497-512.
- Andrade T., Rodrigues H., Bourguignon M., and Codeiro, T. (2015). the Exponentiated Generalized Gumbel distribution."RevistaColombiana",38(1):123-143.
- Nadarajah S., and Kotz S. (2003) The exponentiatedFréchet distribution, Statisticson the Internet. http://interstat.statjournals.net/YEAR/2003/articles/0312002.pdf
- Oguntunde P. E., Adejumo A. O., and Balogun O. S. (2014). Statistical properties of theexponentiated generalized inverted exponential distributions. "Applied Mathematics",4(2):47-55.
- ElbatalI., and Muhammed H. Z. (2014). exponentiated generalized inverted exponential distributions."Applied Mathematics Sciences",8(81):3997-4012.
- Kenney J. F. and Keeping E. S. (1962). Mathematics of Statistics, Part 1, 3rd edition.VanNostrand, New Jersey
- Moors J. J. (1988). A quantile alternative for kurtosis, "Journal of the Royal Statistical Society", Series D37: 25–32.

 (Abd-Elfattah A. M.)
(Abd-Elfattah A. M.)  (Assar S. M.)
(Assar S. M.)