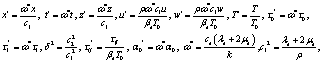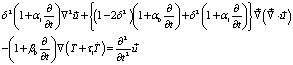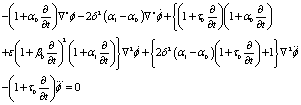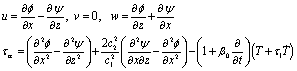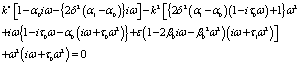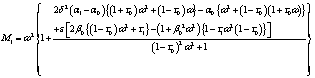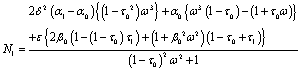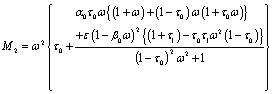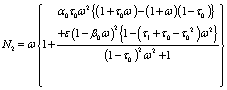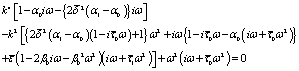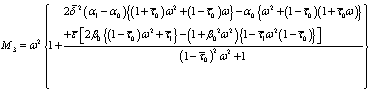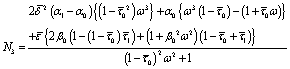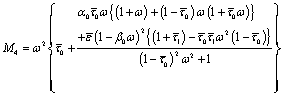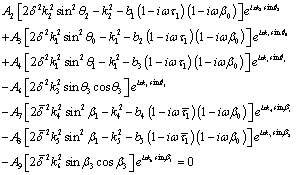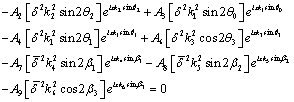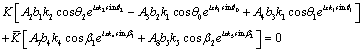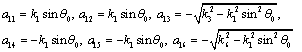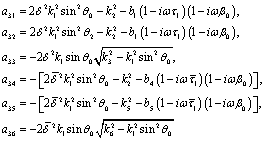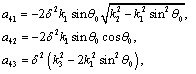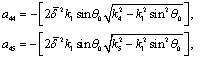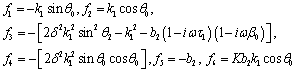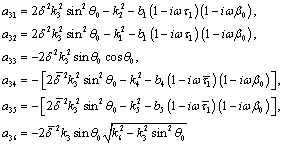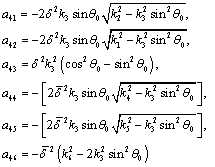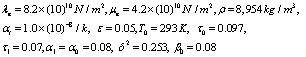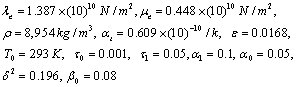Reflection and Refraction of Generalized Visco-Thermoelastic Waves at an Interface Between Two Half Spaces
Sutapa Santra1, A. Lahiri2, N. C. Das2
1Department of Mathematics, Gargi Memorial Institute of Technology, Baruipur, Kolkata
2Department of Mathematics, Jadavpur University, Jadavpur, Kolkata
Email address

(S. Santra)

(A. Lahiri)

(N. C. Das)
Citation
Sutapa Santra, A. Lahiri, N. C. Das. Reflection and Refraction of Generalized Visco-Thermoelastic Waves at an Interface Between Two Half Spaces. Computational and Applied Mathematics Journal. Vol. 2, No. 1, 2016, pp. 12-22.
Abstract
The reflection and refraction due to generalized thermoelastic incident P- and SV- waves at a plane interface between two dissimilar half spaces of visco-thermoelasitic materials have been investigated. Magnitude of coefficient ratios for both the cases of P- and SV- waves have been found out. Several graphs have been drawn to study the nature of variation of the amplitude ratios when the angle of incidence varies. Thermal and viscous effects are compared with the corresponding classical elastic cases.
Keywords
Reflection, Refraction, Visco-Thermoelastic Waves, P-wave, SV-wave
1. Introduction
Biot [1] established the formulation of the classical coupled dynamic theory of thermoelasticity in which the coupling of strain and temperature fields is taken into account. Chadwick [2] solved a few dynamical problems which exhibit the characteristic features of the linear as well as non-linear versions of the theory. Other significant work following this theory are due to Nowacki [3], Parkus [4], Nowinski [5], Kovalenko [6], Boley and Wiener [7], Sneddon [8], Paria [9] etc. In each of the work, the energy equation is of parabolic type resulting parabolic type of heat transport equation. As a consequence, infinite speed of propagation of thermal disturbance is predicted, which is unrealistic from the practical point of view. The equation of motion in this context is hyperbolic in nature and as such predicts finite speed of propagation of the elastic disturbances. Experimental investigations conducted by Ackerman [10], Roger [11], Jackson and Walker [12] etc. for example, have shown that heat pulses do propagate with finite speed. In order to eliminate the paradox of infinite speed of propagation of thermal disturbance, the first generalized mathematical model is presented by Lord and Shulman (L-S) [13], in which the classical Fourier heat conduction equation has been modified by introducing a parameter called ‘relaxation time’, and the heat transport equation becomes hyperbolic in nature and thus finite speed of propagation of heat pulses is predicted. Green and Lindsay (G-L) [14] put forward another model in which the Fourier law of heat conduction remains unchanged whereas the classical energy equation and the constitutive equation are modified by introducing temperature-rate-dependent terms. In G-L model two relaxation time parameters are involved. Another theoretical model on this subject is due to Green and Nagdhi (G-N) [15-17] who provided sufficient basic modification in this constitutive equations that permit treatment of a much wider class of
heat flow problems. Following these generalized theories a host of papers of different nature are being published exhibiting thermoelastic interactions. So far as the presented authors are aware very few papers are published where the reflection of waves in a half space or reflection and refraction in a bonded half spaces are concerned. Sinha et al. [18] considered the reflection and refraction of thermoelastic waves at an interface of two semi-infinite media following G-L model theory. Sharma et al. [19] investigated the problem of generalized thermoelastic wave reflection from the insulated and isothermal stress free as well as rigidly fixed boundary. Singh and Tomar [20] considered the problem of plane waves in thermoelastic materials with voids. Das et al. [21] solved the problem of reflection of generalized thermoelastic waves from isothermal and insulated boundaries of a half space in a different approach. Lahiri et al. [22] considered the reflection and refraction at an interface between two semi infinite media following G-L model. In the present paper, we have considered the reflection and refraction of P- and SV- waves at a plane interface between two dissimilar half spaces of visco-thermoelastic materials. The results in different cases have been analyzed and presented graphically.
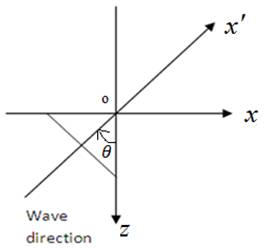
Fig. 1. Intersection of the wave front by 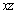 -plane.
-plane.
2. Basic Equations and Formulation of the Problem
In absence of thermal field when an elastic wave reaches a boundary between two media, in general, four waves are generated. Two of these are refracted into the second medium, and two are reflected back. If a thermoelastic incident wave is considered then two additional waves result in due to reflection and refraction respectively.
The basic equations for the study of these waves may be presented as follows:
Let the origin of the rectangular Cartesian coordinate system be fixed on the boundary of the homogeneous, isotropic elastic half space with 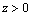 axis directed normally inside the medium with
axis directed normally inside the medium with 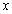 -axis along the horizontal direction. The axis of
-axis along the horizontal direction. The axis of 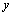 is taken in the direction of the line of intersection of the plane wave front with the plane surface (Fig. 1). If we restrict our analysis to the plane strain in the
is taken in the direction of the line of intersection of the plane wave front with the plane surface (Fig. 1). If we restrict our analysis to the plane strain in the 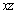 -plane, then all the field variables may be taken as functions of
-plane, then all the field variables may be taken as functions of 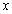 ,
, 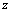 and
and 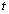 . The displacement vector
. The displacement vector 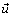 and temperature T may be taken as
and temperature T may be taken as 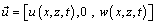 ,
, 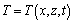 .
.
Following GL-model of generalized thermoelasticity, the equations of motion in absence of body force; the heat conduction equation in absence of heat source; and the stress-strain relation for an isotropic, homogeneous, thermally conducting viscoelastic solid, may be taken as
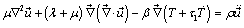 (1)
(1)
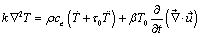 (2)
(2)
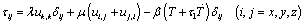 (3)
(3)
where 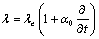 ,
, 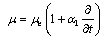 are Lame constants;
are Lame constants; 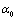 and
and 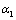 are viscoelastic constants;
are viscoelastic constants;
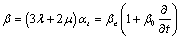 ,
, 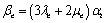 ,
, 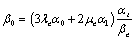 ;
; 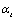 is the linear thermal expansion;
is the linear thermal expansion; 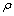 and
and 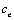 are the density and specific heat at constant strain respectively; k is the thermal conductivity; T is the temperature change;
are the density and specific heat at constant strain respectively; k is the thermal conductivity; T is the temperature change; 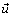 is the displacement vector;
is the displacement vector; 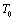 is the reference temperature;
is the reference temperature; 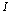 is the unit vector;
is the unit vector; 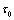 and
and 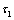 are relaxation parameters satisfying the inequality:
are relaxation parameters satisfying the inequality: 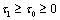 ; a superposed dot represents differentiation with respect to time variable. Equations (1) and (2) are hyperbolic in nature and as such both the viscoelastic and thermal disturbances propagate with finite speed.
; a superposed dot represents differentiation with respect to time variable. Equations (1) and (2) are hyperbolic in nature and as such both the viscoelastic and thermal disturbances propagate with finite speed.
In order to non-dimensionalize the above equations, we define the following quantities:
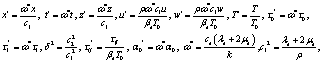
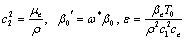 (4)
(4)
Introducing (4) in equations (1)- (3) and suppressing the primes, we obtain
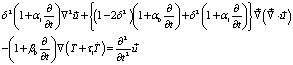 (5)
(5)
 (6)
(6)
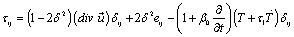 (7)
(7)
Let us consider a decomposition of the displacement vector in the form:
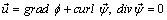 (8)
(8)
where 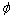 and
and 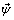 are the thermoelastic potential functions representing P- and SV- wave respectively. Submitting (8) in (5) - (6), we obtain the following equations:
are the thermoelastic potential functions representing P- and SV- wave respectively. Submitting (8) in (5) - (6), we obtain the following equations:
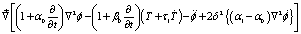
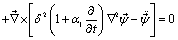 (9)
(9)
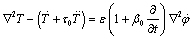 (10)
(10)
Equation (9) will be satisfied if
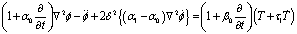 (11)
(11)
and
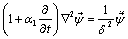 (12)
(12)
From equation (11) and (12) we notice that the P-wave is affected in the presence of the thermal field while SV-wave remains unaffected.
Eliminating T from the equations (10) and (11), we get
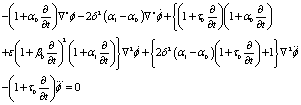 (13)
(13)
Choosing 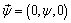 , the equation (12) takes the form
, the equation (12) takes the form
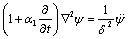 (14)
(14)
Thus the potential 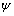 correspond to the displacement in the
correspond to the displacement in the  -plane due to SV-wave. We now write down the displacement components and the stresses in terms of the potential functions as follows:
-plane due to SV-wave. We now write down the displacement components and the stresses in terms of the potential functions as follows:
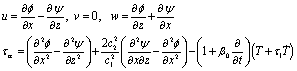
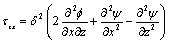 (15)
(15)
For plane P-wave propagating in 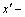 direction (as in Fig. 1) we have
direction (as in Fig. 1) we have
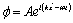
where, k is the wave number and 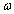 is the circular frequency of the wave. Now
is the circular frequency of the wave. Now 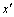 can be calculated as
can be calculated as
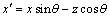
where 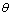 is the angle of inclination of the incident wave with the normal to the surface. Thus
is the angle of inclination of the incident wave with the normal to the surface. Thus 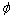 becomes
becomes
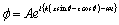 (16)
(16)
Substituting (16) in (13), we get a quadratic equation in  as
as
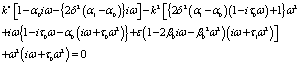 (17)
(17)
Considering the coupling factor 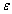 be small, the roots of the equation (17) can be calculated as
be small, the roots of the equation (17) can be calculated as
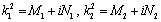 (18)
(18)
where
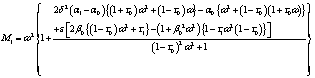
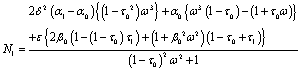
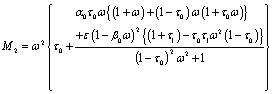
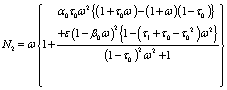
In the same way we can also write down the solution of (16) as
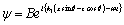
where 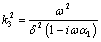 (19)
(19)
3. Case I: Plane P-wave Incident Upon a Plane Surface
Let the angle of incidence with the normal to the surface be 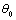 . Other angles are the angle of reflections of P-wave, thermal wave, and SV-wave respectively with the surface normal (See Fig. 2). Then for the P-wave, we may take the following forms:
. Other angles are the angle of reflections of P-wave, thermal wave, and SV-wave respectively with the surface normal (See Fig. 2). Then for the P-wave, we may take the following forms:
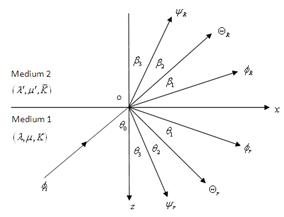
Fig. 2. Incident P-wave and corresponding reflected waves.
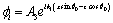 (20)
(20)
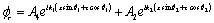 (21)
(21)
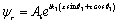 (22)
(22)
where, the suffix i and r correspond to incident and reflected waves respectively. The term 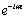 has been omitted from the equations (20) - (22) for simplicity.
has been omitted from the equations (20) - (22) for simplicity.
Since 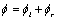 , so
, so 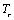 can now be calculated from equation (10) as
can now be calculated from equation (10) as
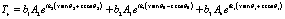 (23)
(23)
where 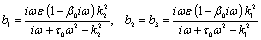 (24)
(24)
If all the above equations refer to the medium 1, then the corresponding counterparts of 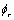 ,
, 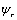 and
and 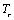 denoted as
denoted as 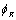 ,
, 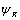 and
and 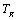 respectively for the medium 2 may be written as:
respectively for the medium 2 may be written as:
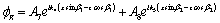 (25)
(25)
where 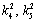 are the roots of the quadratic equation in
are the roots of the quadratic equation in  as follows:
as follows:
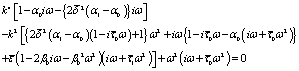 (26)
(26)
where 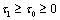 . The counter part of equation (14) is
. The counter part of equation (14) is
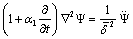 (27)
(27)
The solution of (27) may be written as
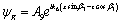 (28)
(28)
where, 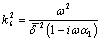 (29)
(29)
The suffix R corresponds to refracted (distorted) wave. 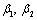 and
and 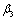 are the angles of the refracted wave directions with the normal to the surface (see Fig. 2).
are the angles of the refracted wave directions with the normal to the surface (see Fig. 2).
The quantities 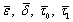 refer to the material parameters of medium 2 corresponding to
refer to the material parameters of medium 2 corresponding to 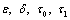 of medium 1. Using (25) we calculate
of medium 1. Using (25) we calculate 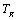 as:
as:
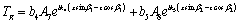 (30)
(30)
where 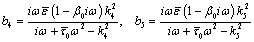 (31)
(31)
Considering the coupling factor 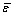 be small, the roots of the equation (26) can be calculated as
be small, the roots of the equation (26) can be calculated as
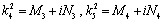 (32)
(32)
4. Boundary Conditions
In order to determine the amplitude ratios we now proceed to apply the boundary conditions as follows:
At the interface, the mechanical boundary conditions require that on the boundary the normal and tangential displacements and stresses must be equal. We write them as
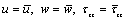 and
and 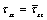 on
on 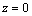 . (33)
. (33)
As in Lavrentyev and Rokhlin [23] the thermal boundary conditions require:
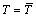 and
and 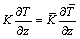 on
on 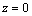 . (34)
. (34)
It may be mentioned that the boundary conditions on the interface (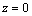 ) are independent of
) are independent of 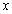 and
and 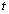 , so the value of the phase velocity and the wave number in
, so the value of the phase velocity and the wave number in 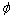 and
and 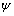 must be the same as those in
must be the same as those in 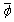 and
and 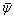 as assumed in the forgoing analysis.
as assumed in the forgoing analysis.
Making use of the potential functions as in (15), we now apply the boundary conditions (33) - (34), where we have taken for Medium 1
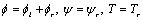 (35)
(35)
and for medium 2 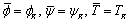 . (36)
. (36)
Thus the boundary conditions (33) and (34) give rise to six equations as follows:
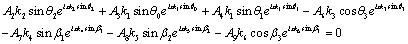 (37)
(37)
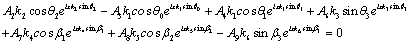 (38)
(38)
In order that the equations (37)-(42) might hold for all values of 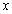 , the terms in the left hand side should be independent of
, the terms in the left hand side should be independent of 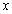 , and this condition is satisfied if
, and this condition is satisfied if
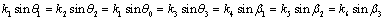 (43)
(43)
Using the conditions as in (43) in the equations (37)- (42) we get a set of six homogeneous linear equations in the seven unknowns 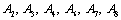 and
and 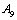 . Hence we prefer to determine the ratios of the amplitudes
. Hence we prefer to determine the ratios of the amplitudes 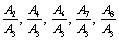 and
and 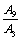 of the P-waves by solving the set of linear equations of the form:
of the P-waves by solving the set of linear equations of the form:
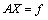 (44)
(44)
where, 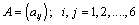
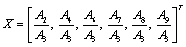 and
and 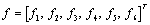
The coefficients of A and the components of 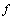 are as follows:
are as follows:
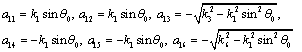
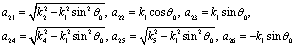
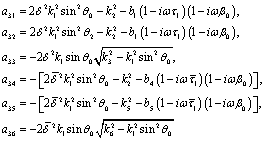
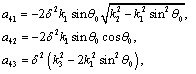
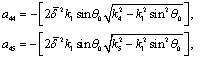
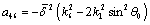
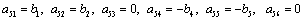
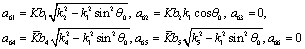
and
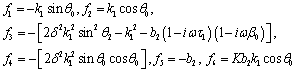
In the above expressions, we have written the coefficient 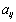 in terms of the angle of incidence
in terms of the angle of incidence 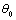 by using (43).
by using (43).
We now solve the system of equations (44) for the six amplitude ratios by pivotal condensation method and shall present some of them in graphs for varying values of the initial angle of incidence 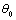 and analyze them in the concluding section.
and analyze them in the concluding section.
5. Case II: Plane SV-wave Incident Upon the Interface
We now proceed to determine the amplitude ratios for an incident SV- wave at the interface see Fig. 2 under the same boundary conditions as in the previous section.
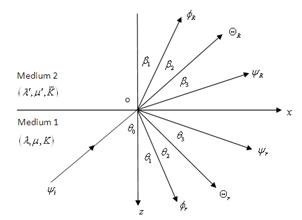
Fig. 3. Incident SV- wave.
We take the incident SV- wave in the medium 1 as (omitting 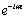 )
)
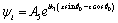 (45)
(45)
Reflected SV-, P-, and thermal waves in the same medium may be taken as
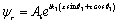 (46)
(46)
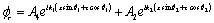 (47)
(47)
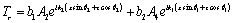 (48)
(48)
Refracted SV-, P-, and thermal waves in the upper medium may be written as
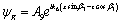 (49)
(49)
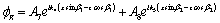 (50)
(50)
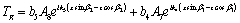 (51)
(51)
where, 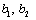 and
and 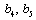 are given in equations (24) and (31) respectively.
are given in equations (24) and (31) respectively.
In this case 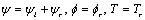 for Medium 1 and
for Medium 1 and 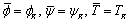 for medium 2. Using equations (24) and (31) we calculated the values of
for medium 2. Using equations (24) and (31) we calculated the values of 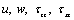 from equations (15) and substituting these values in the boundary conditions (33) and (34) we arrive at the following form of the system of linear equations for the unknown amplitude ratios in the same way as done in the previous section as:
from equations (15) and substituting these values in the boundary conditions (33) and (34) we arrive at the following form of the system of linear equations for the unknown amplitude ratios in the same way as done in the previous section as:
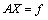 (52)
(52)
where, 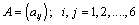
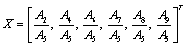 and
and 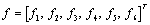
The same argument as in derivation of (43) has been followed in this case also and we get corresponding to (43) the following relations:
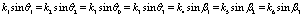
The coefficients are:
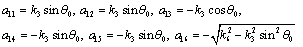
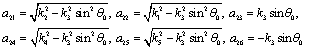
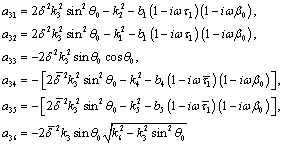
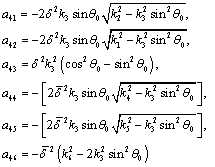
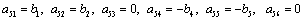
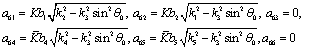
and
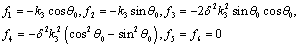
6. Numerical Computations and Analysis of the Result
The coefficients 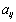 clearly indicate that the amplitude ratios depend on the direction of
clearly indicate that the amplitude ratios depend on the direction of 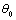 and frequency
and frequency 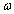 .
.
With a view of illustrating and comparing the results for the different cases following the theory on the model of Green-Lindsay (G-L) and coupled thermoelasticity (CTE), we now depict some graphs and analyze our results. For this purpose, a copper like viscoelastic media (M1) and (M2) are taken as the lower half space and upper half space media.
Four types of graphs representing
i) Classical coupled thermoelasticity (CCTE) :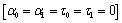
ii) Classical visco-thermoelasticity (CVTE) : 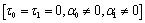
iii) Generalized Temperature rate dependent thermoelasticity (TRDTE) : 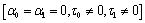 and
and
iv) Generalized Temperature rate dependent visco-thermoelasticity (TRDVTE) : 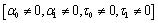
are displayed for the comparison of the nature of their characteristics among each other for both the cases of P- and SV- waves.
As in Sharma and Chand [24], Mallik and Kanoria [25] the values taken as the material parameters in the two media are as follows:
For medium 1 (M1):
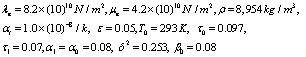
For medium 2 (M2):
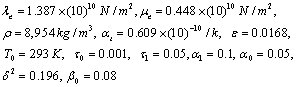
Since the coefficient ratios are dependent on the initial angle of incidence 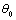 and the frequency of the wave
and the frequency of the wave 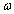 , we prefer to draw the graphs of coefficient ratios for reflections and refraction with respect to the initial angle of incidence
, we prefer to draw the graphs of coefficient ratios for reflections and refraction with respect to the initial angle of incidence 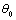 with the choice of
with the choice of 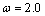 for P-wave and
for P-wave and 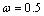 for SV-wave.
for SV-wave.
7. Incident P-wave
Fig. 4 shows that the value of the amplitude ratio 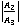 is gradually decreasing with the increase in incident angle for allthe casesi.e. CCTE, CVTE, TRDTE and TRDVTE. The amplitude ratio
is gradually decreasing with the increase in incident angle for allthe casesi.e. CCTE, CVTE, TRDTE and TRDVTE. The amplitude ratio 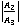 for the four cases CCTE, CVTE, TRDTE, TRDVTE assumes the value 130.2, 121.4, 131.3, 120.8 for
for the four cases CCTE, CVTE, TRDTE, TRDVTE assumes the value 130.2, 121.4, 131.3, 120.8 for 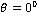 and 127.6, 118.2, 127.6, 116.3 for
and 127.6, 118.2, 127.6, 116.3 for 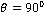 respectively.
respectively.
The amplitude ratio 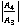 (as in fig. 5) for all the four cases increases sharply and the maximum values are 8.156, 7.228, 8.042, 6.922 occurring at
(as in fig. 5) for all the four cases increases sharply and the maximum values are 8.156, 7.228, 8.042, 6.922 occurring at 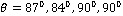 for CCTE, CVTE, TRDTE, TRDVTE respectively.
for CCTE, CVTE, TRDTE, TRDVTE respectively.
In fig. 6 the minimum values of the amplitude ratio 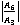 for the case of CCTE, CVTE, TRDTE, TRDVTE are 4.136, 3.841, 4.011, 1.512 at
for the case of CCTE, CVTE, TRDTE, TRDVTE are 4.136, 3.841, 4.011, 1.512 at 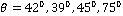 respectively.
respectively.
In fig. 7 the amplitude ratio 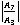 for all the four cases gradually increases.
for all the four cases gradually increases.
The nature of the fig. 8 and fig. 9 is nearly identical. At 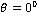 the amplitude ratio
the amplitude ratio 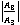 and
and 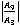 for all the four cases converges to 0.5909 and 1.706 respectively. There is practically no variation in
for all the four cases converges to 0.5909 and 1.706 respectively. There is practically no variation in 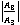 and
and 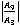 up to
up to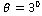 . The amplitude ratio
. The amplitude ratio 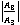 and
and 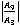 attain maximum values for the cases CCTE, CVTE, TRDTE, TRDVTE are 12.75, 12.21, 11.61, 3.231 at
attain maximum values for the cases CCTE, CVTE, TRDTE, TRDVTE are 12.75, 12.21, 11.61, 3.231 at 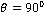 and 41.25, 38.1, 36.35, 11.21 at
and 41.25, 38.1, 36.35, 11.21 at 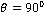 respectively.
respectively.
8. Incident SV-wave
In fig. 10, fig. 11 and fig. 13, the nature of variation of the amplitude ratio 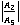 ,
,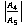 and
and 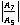 w.r.t
w.r.t 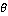 is nearly identical. In fig. 10 and fig. 11, the values of the amplitude ratio
is nearly identical. In fig. 10 and fig. 11, the values of the amplitude ratio 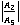 and
and 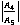 gradually increase up to
gradually increase up to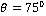 and
and 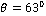 respectively. Maximum value for the amplitude ratio
respectively. Maximum value for the amplitude ratio 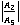 is 1235 at
is 1235 at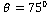 for all the four cases and that for the amplitude ratio
for all the four cases and that for the amplitude ratio 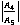 is 1143 for CVTE & TRDVTE and it is 1102 for CCTE & TRDTE at
is 1143 for CVTE & TRDVTE and it is 1102 for CCTE & TRDTE at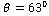 . In fig. 13 the amplitude ratio
. In fig. 13 the amplitude ratio 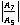 does not show any variation up to
does not show any variation up to 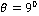 then it increases and attains a maximum value of 284.8 for the case of CVTE & TRDVTE and 275.8 for the case of CCTE & TRDTE at
then it increases and attains a maximum value of 284.8 for the case of CVTE & TRDVTE and 275.8 for the case of CCTE & TRDTE at 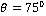 .
.
In fig. 12, the amplitude ratio 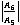 attains minimum value for the case of CCTE, CVTE, TRDTE, TRDVTE of 57.83, 23.02, 54.73, 44.86 at
attains minimum value for the case of CCTE, CVTE, TRDTE, TRDVTE of 57.83, 23.02, 54.73, 44.86 at 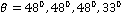 respectively.
respectively.
In fig. 14, the amplitude ratio 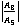 attains 203.2, 203.2, 184.4, 58.67 at
attains 203.2, 203.2, 184.4, 58.67 at 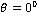 for the case of CCTE, CVTE, TRDTE, TRDVTE respectively and after that it gradually decreases and converges to 3.191 at
for the case of CCTE, CVTE, TRDTE, TRDVTE respectively and after that it gradually decreases and converges to 3.191 at 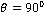 .
.
In fig. 15, the amplitude ratio 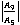 converges to 396.4 at
converges to 396.4 at 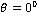 and attains maximum values of 4851, 4851, 4375 at
and attains maximum values of 4851, 4851, 4375 at 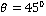 and after that it again converges to 138.6 at
and after that it again converges to 138.6 at 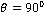 . For TRDVTE, the amplitude ratio attains a maximum value of 1431 at
. For TRDVTE, the amplitude ratio attains a maximum value of 1431 at 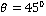 .
.
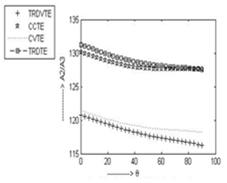
Fig. 4. Variation of A2/A3 for incident P-wave for insulated boundary.
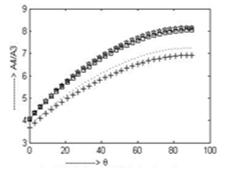
Fig. 5. Variation of A4/A3 for incident P-wave for insulated boundary.
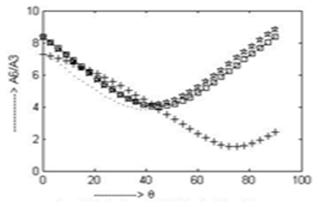
Fig. 6. Variation of A6/A3 for incident P-wave for insulated boundary.
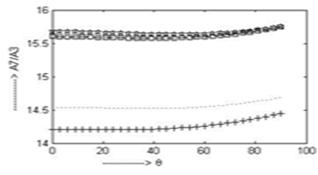
Fig. 7. Variation of A7/A3 for incident P-wave for insulated boundary.
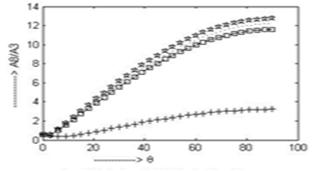
Fig. 8. Variation of A8/A3 for incident P-wave for insulated boundary.
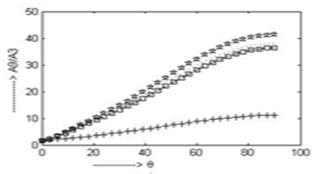
Fig. 9. Variation of A9/A3 for incident P-wave for insulated boundary.
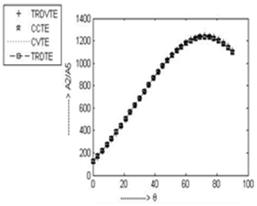
Fig. 10. Variation of A2/A5 for incident SV-wave for insulated boundary.
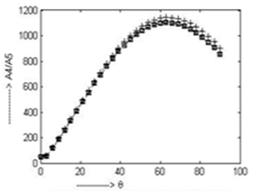
Fig. 11. Variation of A4/A5 for incident SV-wave for insulated boundary.
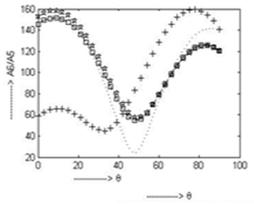
Fig. 12. Variation of A6/A5 for incident SV-wave for insulated boundary.
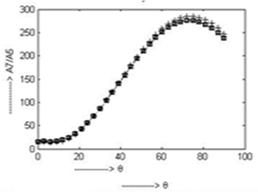
Fig. 13. Variation of A7/A5 for incident SV-wave for insulated boundary.
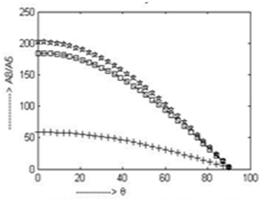
Fig. 14. Variation of A8/A5 for incident SV-wave for insulated boundary.
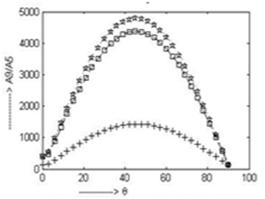
Fig. 15. Variation of A9/A5 for incident SV-wave for insulated boundary.
9. Conclusion
The analytical expressions of the coefficient ratio for both the cases when a P-wave or SV-wave is incident on the boundary of two different bonded medium show that they depend on the initial angle of incidence as well as the frequency of the waves. Apart from the thermal effects it is noticed that the viscoelastic character imparts significant effects as pronounced in the curves for different coefficient ratios both for reflected and refracted phenomena.
Reflection is always represents in terms of reflection coefficient and is defined by as the ratio of the reflected and incident wave amplitudes ie,
Reflection Coefficient (R) =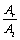 ,
,
Where 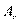 and
and 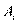 are reflected and incident wave amplitudes respectively. The magnitude of the reflection coefficient is the relation between the magnitudes of reflection from the interface between two medium with different physical properties. The impedance Z of the two medium depends on the magnitude of reflection from the boundary, Z=
are reflected and incident wave amplitudes respectively. The magnitude of the reflection coefficient is the relation between the magnitudes of reflection from the interface between two medium with different physical properties. The impedance Z of the two medium depends on the magnitude of reflection from the boundary, Z= 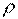 v, where v is the thermalvelocity of the medium.
v, where v is the thermalvelocity of the medium.
The expression of the reflection coefficient and incident angle αi is:
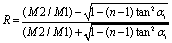 ,
,
Where 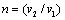
Where 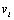 ,
, 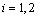 are the velocities of two mediums.
are the velocities of two mediums.
Since the energy is always constant and absorption is not negligible the remaining energy must be transmitted into the other medium and will be refracted since the velocities of the two medium are different.
For the above reason partitioning of energy in the form of amplitude ratios of reflected and transmitted waves is not obeying law of conservation of energy in most of the figures.
Acknowledgement
The authors are thankful to DST-PURSE programme of the Department of Mathematics, Jadavpur University, Kolkata- 700 032.
References
- M. Biot, Thermoelasticity and Irreversible Thermodynamics, J. Appl. Phys., vol. 27, 240-253, 1956.
- P. Chadwick, I. N. Sneddon, Plane Waves in an Elastic Solid Conducting Heat, J. Mech. Phys. Solids, vol. 6, 223-230, 1958.
- W. Nowacki, Some Dynamic Problems of Thermoelasticity, Archiwum Mechaniki Stosowanej, vol. 11, No. 6, 737-750, 1959.
- H. Parkus, Stress in a Centrally Heated Disc, Proc. 2nd U. S. Nat. Congr. Appl. Mech., 307, 1954.
- J. L. Nowinski, W. Olszak and W. Urbanowski, On the Thermoelastic Problem in the Case of Bodies of any type of Curvilinear Orthotropy, Archiwum Mechaniki Stosowanej, vol. 7, No. 2, 247-265, 1955.
- A. D. Kovalenko, Thermoelasticity, Wolters Noordhoff, Groringen,1969.
- B. A. Boley and J. H. Weiner, Theory of Thermal Stresses, John Wiley, N. Y., 1960.
- I. N. Sneddon, Fourier Transforms, McGrawHill Book Company, inc. 1951.
- G. Paria, Coupling of Elastic and Thermal Deformations, Appl. Sci. Res.: sec. a, 7, 463-475, 1959.
- C. C. Acherman, B. Bentman, H. A. Fairbank and R. A. Guyer, Second Sound in Solid Helium, Phys. Rev. Lett., vol. 16, 789-791, 1966.
- S. J. Rogers, Transport of Heat and Approach to Second Sound in Some Isotropically Pure Alkali-Halide Crystals, phys. Rev. b, 3, 1440-1457, 1971.
- H. F. Jackson, C. T. Walker, Thermal Conductivity, Second Sound and Phonon-Phonon Interactions in NaF, Phys. Rev. b, 3, 1428-1439, 1971.
- H. W. Lord and Y. Shulman, A Generalized Dynamic Theory of Thermoelasticity, J. Mech. Phys. Solids, vol. 15, 299-309, 1967.
- A. E. Green and K. A. Lindsay, Thermoelasticity, Journal of Elasticity, vol. 2, 1-7, 1972.
- A. E. Green and P. M. Naghdi, A Re-examination of the Basic Postulate of Thermomechanics, Proc, Roy soc., London Ser. A, vol. 432, 171-194, 1991.
- A. E. Green and P. M. Naghdi, On Undamped Heat Waves in an Elastic Solid, J. Thermal stresses, vol. 15, No. 2, 253-264, 1992.
- A. E. Green and P. M. Naghdi, Thermoelasticity without Energy Dissipation, J. Elasticity, vol. 31, 189-208, 1993.
- S. B. Sinha, and K. A. Elsibai, Reflection and Refraction of Thermoelastic Waves at an Interface of Two Semi-infinite Media with Two Relaxation Time, J. Thermal stresses, vol. 20, 129-146, 1997.
- J. N. Sharma, V. Kumar and Dayal Chand, Reflection of Generalized Thermoelastic Waves from the Boundary of a Half Space, J. of Thermal Stresses, 26: 10, 925-942, 2003, DOI: 10.1080/01495730306342.
- J. Singh and S. K. Tomar, Plane Waves in a Rotating Generalized Thermoelastic Solid with Voids, Int. Jour. Engg. Sc. and Tech., vol. 3, No. 2, 34-41, 2011.
- N. C. Das, A. Lahiri, S. Sarkar, and S. Basu, Reflection of Generalized Thermoelastic Waves from Isothermal and Insulated Boundaries of Half Space, J. Computers and Mathematics with Applications, vol. 56, 2795-2804, 2008.
- A. Lahiri, N. C. Das, M. B. Bera and S. Basu, Reflection and Refraction of Generalized Temperature Rate Dependent Thermoelastic Waves at an Interface Between Two Semi-infinite Media, Int. J. of Applied Mechanics and Engineering, vol. 16, No. 4, 1051-1069,2011.
- A. I. Lavrentyev and S. I. Rokhlin, Anomalous Attenuation Effect on Reflectivity of an Ultrasonic Wave from a Thin Layer Between Dissimilar Materials, J. Acoust. Soc. Am., vol. 101, No. 6, 3405- 3414, 1997.
- J. N. Sharma and Rattan Chand, Transient Thermoviscoelastic Waves in a Half – space due to Thermal Loads, Journal of Thermal Stresses, vol. 28, 233-252, 2005.
- S. H. Mallik and M. Kanoria, Generalized Thermoelastic Functionally Graded Solid with a Periodically Varying Heat Source, International Journal of Solids and Structures, vol. 44, 7633-7645, 2007.

 (S. Santra)
(S. Santra)  (A. Lahiri)
(A. Lahiri)  (N. C. Das)
(N. C. Das)