Investigating Twin Prime Numbers with Mathemagical Twin Black Hole

Mi Zhou, Jun Steed Huang, Zhiqiang Zuo

Suqian College, Jiangsu University, South Huanghe, Jiangsu, P. R. China

Email address

Citation

Mi Zhou, Jun Steed Huang, Zhiqiang Zuo. Investigating Twin Prime Numbers with Mathemagical Twin Black Hole. Computational and Applied Mathematics Journal. Vol. 2, No. 3, 2016, pp. 29-33.

Abstract

Based on the digital black hole findings, this paper provided a novel method for investigating the heated twin prime number issues. That is, writing down the prime numbers in sequence, counting the number of the twin prime numbers, the total number of the prime numbers and the sum of these two numbers from the given natural numeric string of any section length of any prime region respectively. After iteration repeatedly, the finally result will certainly fall into the black hole of either 000 or 022, testifying that there are infinite numbers of twin prime numbers out of the related prime number section of traditional sqaure regions. This new special method deals with the problem of twin prime numbers easily and effectively, with potential application for random number generation for digital media security.

Keywords

Twin Primes, Mathemagical Twin Black Holes, Kaprekar Numbers, Digital Storage

1. Introduction

One of the old problems of the twin prime numbers is that "whether there exists an infinite number of twin prime numbers or not". At present, the best achievement is made by Yitang Zhang [1]. Dr Zhang proved that there is an n less than or equal to 70, 000, 000 such that p, p+n are primes, making a great contribution to the twin prime conjecture as verified by Prof. H. Iwaniec, a famous number theory mathematician [2]. Goldston defined the primes as the natural or counting numbers with exactly two factors, namely 1 and themselves, or equivalently the prime numbers [3].

Albrecht and Firedrake described the theory of Mathemagical Black Holes that apply a step-by-step procedure to the starting number and get a new number, and if the new number is the same as the previous number, then this number is a mathemagical black hole [4]. Jones invented the Kaprekar routine when his wife sent him to the supermarket [5]. Siegel showed that subtractive black holes and black loops are generalizations of Kaprekar’s constants, which provided a rich environment for conjecture and proof [6]. Wiegers proposed that the mathematical universe also contains black holes, seemingly innocuous numbers from which no other number can escape [7]. We look into this set of problems for twin prime numbers with a mathemagical black hole point of view. And try to find an application for the new finding.

The main reason that prime number distribution beiing investigated for many years is that the distribution has no pattern at all. It is this very feature, which attracted a number of engineers, due to its patternless property, we are able to construct the pseudo random number generators. The recent works around this topic can be found in references [13] and [14], where the physical random number generatation is using optical chaos, very close to a pure random number generator, which means that the cost will be high. The quantum random number generator can provide the pure randm number, but again the cost of quantum device is even more expensive than the optical chaotic device. As such, we believe that using the prime number to generate the random number is still a cost effective software based method, as long as we select a relatively strong algorithms, like those recommended by NIST [15].

2. About the Kaprekar Constant

The concept of mathemagical black hole is that one arithmetic number begins with the integers, and then the result of repeated iteration inevitably fall into a fixed number (or several of them), the number(s) is(are) called mathemagical black hole(s) or digital black hole(s). In this paper, we defined a so called number theory twin prime black hole, i.e. the rule is derived from the number theory, and the twin prime numbers, i.e. the ending number is not one, but two. The reason behind it is that every prime number pair has a so-called gender, if one is male, the other will be female. We need two black holes to treat each ending gender.

As Kaprekar [8] described, as long as you input a number of three digits with different numbers in each digit rather than 111, 222 as example, then you rank three number in each digit to get the maximum and minimum number respectively according to the order of numerical value. The maximum subtract the minimum to get a new number, which finally become 495 following the method above repeatedly.

For example: input 352 to get the maximum number 532 and the minimum 235 after ranking, 532 minus 235 to 297. Repeat the same arithmetic above continually to get the new number of 693, 594, 495 respectively.

Four digits black hole 6174: Rank the four-digit numbers from small to large and large to small to get the maximum and minimum numeric strings. The maximum number subtracts the minimum number to get a new number. Then repeat the arithmetic procedure above continually. If the four digits are not same, the numeric number string will become 6174 eventually.

For example, 3109, 9310-0139=9171, 9711-1179=8532, 8532-2358=6174. The number of 6174 will also become 6174, 7641-1467=6174.

Take the four-digit number 5679 arbitrarily. Take the method above as follows:

9765-5679==4086, 8640-0486=8172,

8721-1278=7443, 7443-3447=3996,

9963-3699=6264, 6642-2466=4176

7641-1467=6174 one mathemagical black hole:

One mathemagical black hole called even odd black hole can be defined like this: Set up an arbitrary numeric string and count the amount of even number, odd number and total digits of this arbitrarynumeric string,

For example: 1234567890,

Even: count the number of even number of this numeric string, 2, 4, 6, 8, 0 in this case, a total of five.

Odd: count the number of odd number of this numeric string, 1, 3, 5, 7, 9 in this case, a total of five.

Sum: count the amount of this numeric string, a total of ten in this case.

New number: rank the order according to the "even-odd-sum" to get a new number: 5510.

Repetition: make the new number 5510 operated by the arithmetic above to get a new number: 134.

Repetition: make the new number 134 operated by the arithmetic above to get a new number: 123.

Conclusion: make 1234567890 operated by the arithmetic above to finally get 123.

We can make MATLAB programs with a computer and verify the conclusion to finally get 123 after limited repetition. In other words, the final result of the arbitrary number can not escape from the black hole of 123.

3. The Twin Primes and the Twin Black Holes

Similarly we can make following mathemagical twin black hole:

Write down the natural number successively from any starting number and any ending number, and count the twin prime numbers，the number of the prime numbers and the sum of two numbers. The finally result will certainly fall into the black hole of 000 or 022.

For example:

2 3 5-1 3 4- 0 1 1-0 0 0

2 3 5 7-2 4 6-0 1 1-0 0 0

2 3 5 7 11-2 5 7-1 3 4-0 1 1-0 0 0

2 3 5 7 11 13-3 6 9-0 1 1-0 0 0

2 3 5 7 11 13 17-3 7 10- 0 2 2

…………..

Without the exception, the rule is: after the first arithmetic, it is obtained:

X Y X+Y

If Y is the prime number, it will fall into the black hole of 022. If Y is composite number, it will fall into the black hole of 000.

A twin prime is a prime number that is either 2 less or 2 more than another prime number - for example, the twin prime pair (41, 43). In other words, a twin prime is a prime that has a prime gap of two.

In 1849, de Polignac made the more general conjecture that for every natural number k, there are infinitely many primes p such that p + 2k is also prime. The case k = 1 is the twin prime conjecture.

On April 17, 2013, Yitang Zhang announced a proof that for some integer N that is less than 70 million, there are infinitely many pairs of primes that differ by N.[9][10] Zhang's paper was accepted by Annals of Mathematics in early May 2013. [1] Terence Tao subsequently proposed a Polymath Project collaborative effort to optimize Zhang’s bound. [11] As of April 14, 2014, one year after Zhang's announcement, according to the Polymath project wiki, the bound has been reduced to 246, and recently down to 6 by Prof. Tao’s team, under certain conditions.

Twin prime conjecture: there are infinitely many primes p such that p + 2 is also prime

Conditional Proof:

Let’s assume that the twin black holes have no exception for now, we use Matlab conducted the preliminary search, so far we haven’t found any exception. The program (twin black holes) is available for free download at Matlab server. We now assume that there is a finite number of the twin prime numbers. This number is X. Now, we make a list as follows:

X Y X+Y

Y can be arbitrarily large because of infinite prime numbers. If Y is the prime number and the sum of Y and X is the composite number, X must be the prime number, which will fall into the black hole of 022-022. If X is the composite number, it will fall into the black hole of 011-000, which is not the case. Thus, X must be the prime number.

If Y is the composite number, the sum of Y and X is the prime number, X is odd and composite number and the black hole of 011-000 is obtained. If X is the prime number, the black hole of 022 will be obtained, which is not the case. Thus, X must be the composite number.

X can not be prime number and the composite number at the same time, it is contradictory. As such, the assumption that X is finite is incorrect. Therefore, there are countless twin prime numbers!

End of the conditional proof.

4. Simulations

In this section, we will plot the trace of the twin black hole, showing how the numbers in different sqaure regions, defined by 36n(n+1) (n=1, 2, 3…), will fall into the black hole. We pick the 10 strings Sn; the first string is from region R1, the second string is from the region R1 to R2, and so on so forth, the 10^th string is from region R1 to region R10. The region is the conventional prime number region. Here are the plots.

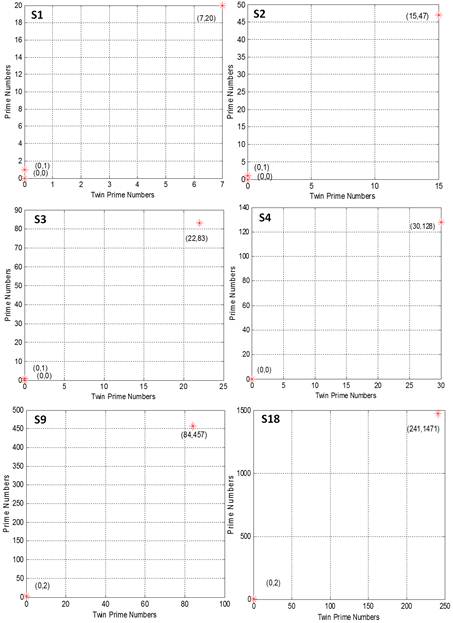
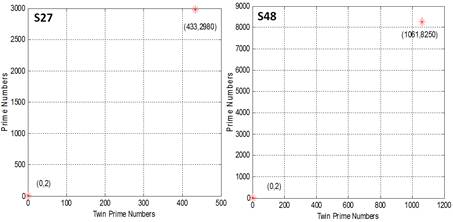
Fig. 1. The trace of the twin black hole made by Matlab program.

S1: 1-72; S2: 1-216; S3: 1-432; S4: 1-720;

S9: 1-3240; S18: 1-123312; S27: 1-27216; S48: 1-84672.

The x-axis is the twin prime numbers, the y-axis is the correspongding prime numbers, from above, where the section ending number is given by 36n(n+1), n is the sequence number of the region for the string section Sn. From which we can see that the most sections fall into the black hole 000, the section number that falls in the 022 black hole is quite random, we can use it to construct the random sequence for encrypting the cloud storage data. Here is the summary table that shows the typical Section and the trace of the string that leading to the twin black holes, where the twin prime distance is defined as the section size divided by the number of twin primes inside the section, e.g. for the first section there are 72 numbers, and 7 twin primes, 72/7=10 roughly is called the average distance. This way, we can calculate the distance, and it should be less than 246 under certain conditions, which worths further investigation.

Note that, the section does not need to be started from R1, it can be from any region, in extreme case, each section can contain only one region, in that case, you will find more sections (regions) fall into the black hole 022, however the distance inside each section grows quickly as the number approach infinite. That is to say, less and less twin primes will be observed as the number becoming large.

Table 1. Presentation of the twin black hole in different prime sections.

5. Conclusion

In this paper, we have proposed a twin black hole constants based on the Kaprekar constants methodology, we further related this mathemagical phenomenon with the twin prime conjecture, we provided a conditional proof of the conjecture, and plotted the trace of the iterations, for the twin prime number region 1 up to region 48. The algorithm can find itself some practical application of preventing the malicious time bomb that could destroy some part of the cloud storage site [12], by using the random property of the fewer black holes 022 campared with the more black holes 000 out of the entire sequence of regions.

References

1. Zhang, Yitang (2014). "Bounded gaps between primes". Annals of Mathematics 179 (3): 1121–1174. doi: 10.4007/annals.2014.179.3.7. MR 3171761.
2. Moh T. T, "Zhang, Yitang’s life at Purdue" (Jan. 1985-Dec, 1991), Mathematics Department, Purdue University, Prime time, Insight, the Science College of Purdue University.
3. D. A. Goldston, Y. Motohashi, J. Pintz, C. Y. Yıldırım, "Small gaps between primes exist", Proc. Japan Acad. Ser. A Math. Sci. 82, no. 4 (2006), 6165.
4. Albrecht, Bob & Firedrake, George (2011) "Mathemagical Black Holes", free ebook, Creative Commons Attribution.
5. Jones Emy, The Kaprekar Routine, July 2008, Master of Arts Thesis for Teaching with a Middle Level Specialization in the Department of Mathematics.
6. Siegel Murray H. (2005). "Subtractive Black Holes And Black Loops" Texas College Mathematics Journal Volume 2, Number 1, Pages 1-9, August 17, 2005 .
7. Wiegers Brandy, (2011) Berkeley Math Circle, April 26, 2011, brandy@msri.org.
8. Kaprekar DR (1980). "On Kaprekar Numbers". Journal of Recreational Mathematics 13 (2): 81–82.
9. McKee, Maggie (14 May 2013). "First proof that infinitely many prime numbers come in pairs". Nature. doi: 10.1038/nature.2013.12989. ISSN 0028-0836.
10. McKee, M. (2013). "First proof that prime numbers pair up into infinity". Nature. doi: 10.1038/nature.2013.12989.
11. Tao, Terence (June 4, 2013). "Polymath proposal: bounded gaps between primes", Polymath Proposals.
12. Brindley D. L, "Filling in a digital black hole", The Observer on Sunday 25 January 2009, from the British Library.
13. Amr Elsonbaty, Salem F. Hegazy, Salah Sabry A. Obayya, "A new technique for ultrafast physical random number generatation using optical chaos", SPIE Photonics Europe 2015.
14. Gabriela Mogos, "Quantum Random Number Generator vs. Random Number Generator", the 11th International Conference on Communications COMM2016.
15. National Institute of Standards and Technology, "NIST Removes Cryptography Algorithm from Random Number Generator Recommendations", 21 April 2014 .