| 1. | ||
| 2. | ||
| 3. | ||
| 4. | ||
| 5. | ||
The Distribution of Periodic Perturbations of the Mass Flow of Gas on an Inclined Site of Gas Pipeline in Isothermal Mode
I. K. Hujaev, Sh. K. Boltibaev*
Laboratory "Modeling of Complex Systems", Center for Development of Software Products and Hardware-Software Complexes, Tashkent, Uzbekistan
Email address
(I. K. Hujaev) 
(Sh. K. Boltibaev) Citation
I. K. Hujaev, Sh. K. Boltibaev. The Distribution of Periodic Perturbations of the Mass Flow of Gas on an Inclined Site of Gas Pipeline in Isothermal Mode. American Journal of Mathematical and Computational Sciences. Vol. 1, No. 1, 2016, pp. 1-9.
Abstract
The analytical decision of a problem on distribution of perturbations of the mass flow of the gas, presented in the form of Fourier series, on a linear site of a gas pipeline under the influence of forces of a friction, gravitation and inertia is received. Thus quasi-one-dimensional equations linearized by I. A. Charny also are presented in the form of the uniform equation concerning pressure and the mass flow. The qualitative analysis of the decision is passed and the separate result of computing experiment under the decision is presented.
Keywords
Modelling of Gas Pipelines, Disturbance Perturbations of Mass Flow of Gas, Analytical Periodic Solution, the Influence of the Forces of Friction and Inertia in the Pipeline
1. Introduction
The work of pneumatic and hydraulic devices on transfer of momentum and energy, the shots made from a weapon in an automatic mode, the work of a jackhammer and many other processes occur in a cyclic mode. In [1] the results of the comparison method of simulation modeling and statistical linearization for the analysis of the statistical properties of the stochastic model of quasi-stationary non-isothermal mode of transporting of natural gas on the linear part of gas pipeline. Method statistical linearization can be used to improve the processing speed, method of simulation modeling provides high precision.
Workload of the main gas pipelines at statistical processing shows daily, weekly and annual repeatability [2]. Mathematical modeling of such processes taking into account the basic factors of forces usually leads to the type of telegraph equation which supposes the solution in linear statement. Below, the system of the equations of gas-dynamic state of an inclined elementary section of a gas pipeline with application of averaging method by Charny I. A. is led to such equation concerning static pressure and the mass flow of gas and solved under conditions when cyclic changes of the mass flow on time are processed on the boundary. A method of solution of a problem offered in this work is useful for cases of other boundary conditions corresponding to the listed above and other periodic processes.
2. Statement of Problem
The problem without initial conditions is stated as follows.
On entrance and exit of the section, which has length of 
, periodic changes of the mass flow of gas are given in the form of Fourier series
, (1)
. (2)
Hereinafter 
– m-th frequency of perturbations; 
– the period of perturbations.
Boundary conditions (1) and (2) can be presented as constant, variable, piecewise constant, piecewise variable values of function or results of experimental data processing [3, 4].
The system of quasi-one-dimensional equations, linearized by Charny I. A., corresponds to isothermal process of transportation of gas with the account of all factors of forces and looks like [5-8]
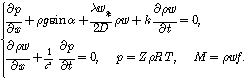(3)
Values of temperature Т, coefficient of supercompressibility Z, gas constant R, characteristic flow speed 
in computational area, diameter of gas pipeline D, the areas of cross-section of a gas pipeline 
and speed of distribution of small perturbations of pressure c we consider as constant parameters. Acceleration of gravitational force g and an average inclination of a gas pipeline from horizon 
are accepted constants (
–leveling height of an axis of the pipeline on cross-section 
). At k=0 the local component of force of inertia of gas is excluded from consideration, and at k=1 – it is considered.
The parameters of gas – pressure р, density 
, the mass flow M and average mass speed w on cross-section of gas pipeline are functions of time t and longitudinal coordinate х.
It is required to find stationary and periodic parts of the solution of the problem.
3. Solution of the Problem
For the solution of the problem we eliminate 
and 
from the system (3) and make the equation relative to mass flow of gas (the similar equation is made also relative to pressure)
. (4)
Here the member with coefficients 
represents the force of friction; and the member with coefficients 
the force of gravitation.
The implementation of the boundary conditions, as equations and conditions are linear, is done in the form of a reduction and superposition of solutions.
The stationary part of the mass flow 
of the whole solution is defined from the second equation of the system (3), in the form 
for stationary statement, in the implementation of the conditions:
.
The equation has a solution only when the condition 
is satisfied. Accordingly, the static part of the mass flow becomes
On the other hand, from the first equation of the system (3) at stationary statement, taking into account the value of mass flow, we have
or
.
The presence of the first derivative from the unknown in this boundary condition means that we need supplementary condition for the determination of the stationary part of the solutions of the task relative to pressure. We consider, that 
is known and search the solution of the equation in the form of
.
Substitution of the solution into the equation leads us to the value of summand
.
The implementation of the boundary condition leads us to the value of coefficient
.
For a horizontal gas pipeline (at 
) the stationary part of pressure in the solution, it is necessary to accept it in the form of
,
which follows from the solution resulted above the equation at limiting transition of 
.
To obtain the non-stationary summands of composed solutions for pressure and mass flow we entered new unknown functions 
and 
corresponding to the fixed frequencies of 
at m=1, 2, 3... In this connection the solution of the problem for pressure takes the form
,
and for the mass flow of gas –
.
At such replacement the equation for separately taken frequency , for example, concerning the components of mass flow, takes a form of
.
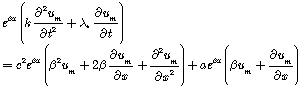Both sides of the equation are simplified by 
. At the same time, we remove the members from the first derivative sought in the space coordinate of х. So we accept the relation 
. Then the equation takes a form of a telegraph equation [9]:
.
For separately taken frequency boundary conditions are transformed and take form of:
The solution is searched with introduction of auxiliary functions in the form of
.
As 
is true, the real part of the solution 
corresponds to the boundary condition 
and an imaginary part 
which have unit amplitude. To find the required solution by using auxiliary functions, it is necessary to multiply the real and imaginary parts of functions by corresponding coefficients of boundary conditions and sum them up [9].
By inserting into the telegraph equation, we receive the ordinary differential equation of the second order with complex coefficient
where 
.
In the exponential form the coefficient of the given equation has a form of
,
where
,
.
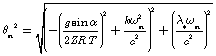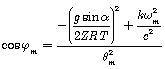The value of 
depends on the sign of 
:
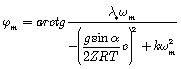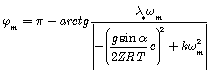when 
when 
.
Since 
by denoting 
, we have 
.
Signs of arithmetic roots of values 
are found from the condition 
, which is true for acceptable values of and 
.
Based on the value of 
solutions of 
are selected in a form of:
.
Separately we construct the solutions for unit amplitude:
– input perturbation 
with conditions: 
– exit perturbation 
with conditions: 
The implementation of input perturbation
leads us to find the values of required coefficients
.
Therefore the solution is to be
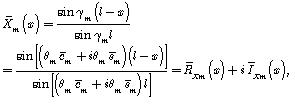
where
,
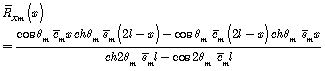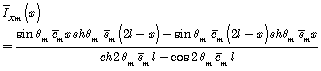
which represent real and imaginary parts of
.
By repeating the procedure for exit perturbation with unit amplitude
we are convinced, that in this case 
and 
. Then by replacing the argument to 
in the expressions 
, we have following relations for exit perturbations
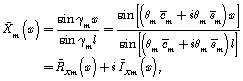
where
,
.
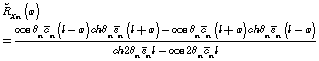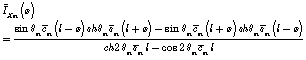We insert the received values of into the solution for
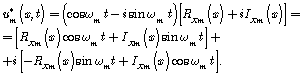
From here we have
for boundary perturbation of 
with unit amplitude
and for –
.
Having provided the unknowns 
with the corresponding overlines and having multiplied them by corresponding coefficients, we have solutions taking into account input and exit perturbations.
Reverse transition to the mass flow gives us:
The solution can be written in an easy form for implementation as follows
Let us proceed to the determination of multiplier 
in a separate component of the solution relative to pressure of gas 
. As noted above, the equation for it takes the form of
.
We compose the boundary conditions for this equation, therefore turn to the first equation of the system (3) and write down it for in the form of
.
By substituting in the left part of the equation we have
,
where the equality 
is considered.
From here at 
it follows
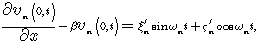
where
.
Similar operations are done for 
and we get
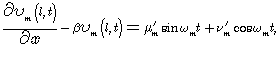
where
Again we introduce auxiliary functions
for input 
and exit 
perturbations with individual amplitude. By using them we obtain the components of as it is done in case .
The factor 
in part of input perturbation 
with unit amplitude is defined according to boundary conditions
and the multiplier 
in part of exit perturbation 
with unit amplitude
Let 
Then we have the following for input perturbation with unit amplitude
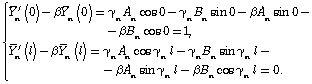
From here it follows
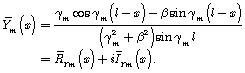
Parts of the solution 
and 
are distinguished, by multiplying numerator and factor of fractional function to conjugation of the doubled denominator 
.
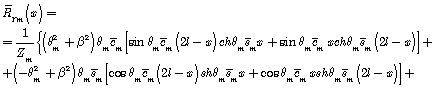
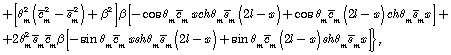
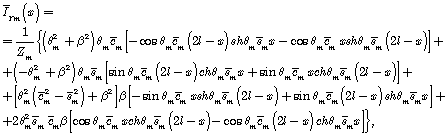
where
Thus, we have obtained the solution for individual input amplitude of the mass flow as a part of pressure
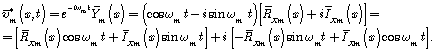
We form the portions of input perturbation of the mass flow in the pressure, corresponding to frequency :
Similarly we find the portions of exit perturbation 
with unit amplitude.
Assume that for exit perturbation the sought function is
The boundary conditions for a part of exit perturbation with unit amplitude are
Realizing these boundary conditions we obtain the solution
here
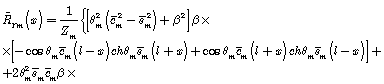
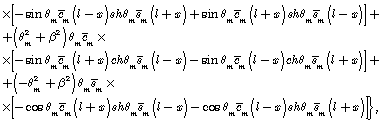
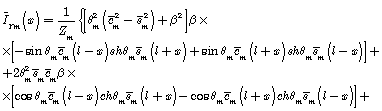
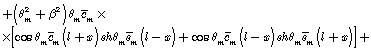
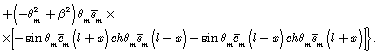
The solution for unit amplitude of exit perturbation makes
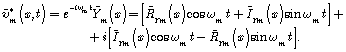
As the first bracket corresponds to , and the second bracket to , having multiplied them to corresponding coefficients and having summed, we have
It is the portion of exit perturbations of the mass flow of gas as a part of the solution of a problem concerning pressure of gas. We make the total solution for pressure of gas
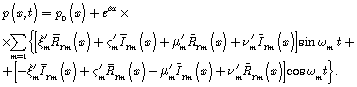
Flow velocity 
is defined under the known formula
.
So, the problem is solved and the values of 
and 
are determined.
4. Discussion of Results
The time variable in solutions is presented by factors and 
, that is typical for periodic processes as a whole. The received solution as a total can describe big and small, including jumping changes of the mass flow of gas in computing area.
The behaviour of the solution for relative to coordinate х can be characterized, based on the values of coefficient
the ordinary differential equation of the second order.
When 
the factors of summands have the form of 
. Such result is expected at zero value of the real part 
, in particular for a horizontal gas pipeline without force of inertia. Actually perturbations decrease in exponential law at removal from the source (borders of section) that is connected to the account of only summands with factors 
for input perturbation and only a summand 
for exit perturbation.
When 
i.e. at 
and 
, the solution of a problem for separate frequency contains factors of a form 
and 
. In this case the discrete step is kept in the solution at distribution of perturbations only from one end of a section and move along the length of a section, transformed only in the end of a section. The case of interaction of opposite perturbations in the field of various forces is the issue of interest.
The case 
corresponds to «seemingly resonance» case: 
. Perturbation linearly increases or decreases depending on the value of coefficient A. With the account of (and without it) the factor is limited to a local maximum in the graph.
These judgments concern separate m-th component of results in limited cases. The similar analysis can be done concerning the pair of forces which represent cases of complex value.
The changes of pressure and the mass flow of gas on a horizontal site of a gas pipeline with a length of 
are presented as an example. On an input we have constant outgo of 
, and in the end of a site gas is consumed as much as possible during the workday (250 kg/s – from 8 o'clock till 17 o'clock and 50 kg/s – the rest of time in a day).
In figure-1 the dynamics of isobars during a day are presented.
In fig. 2 the changes of the mass flow curves for this case are presented.
In case of complex value of , the solution contains factor in the form of 
. It corresponds to sinusoids with decreasing or increasing amplitude.
It is necessary to note, that at considerable slopes of a site from horizon, probably the value of is negative for the first member or for the several first members. Such frequencies result to deeper penetration of perturbations with weak decrease in amplitude.
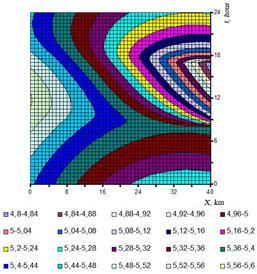
Figure 1. The change of static pressure (in MPa) of gas along the length of gas pipeline during a day with the account of forces of friction and inertia of gas 
, 
, 
, 
, 
, 
, 
, 
, 
, 
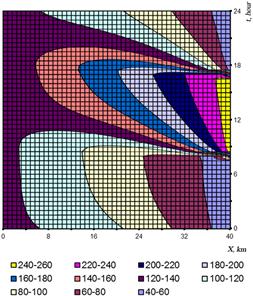
Figure 2. The change of the mass flow of gas (in kg/s) along the length of pipeline during a day with the account of forces of friction and inertia of gas Data see fig. 1.
Generally, the functions 
for the solution concerning the mass flow, and functions 
for the solution concerning static pressure serve as distinctive transfer functions for separately taken frequency. Each case of a combination of factors of forces and each variant of boundary conditions has own components and forms of transfer functions. In conjunction with the stationary components they make up the whole picture of a complex dynamic process of propagation of perturbations of mass flow.
5. Conclusion
The presented material corresponds to the Problem 2 from [10] where the force of resistance of a friction was considered only. On the basis of the method offered in this work we can obtain a solutions of other five problems from [10], and also the problems from [6] taking into account all factors of force and a receiver. Realization of the received solutions in the form of software product allows analyzing gas-dynamic state of gas on a site with the ignorance of separate factors of forces. For example, as already have noted above, at 
the inertial component of force of inertia is not considered; at 
the force of a friction is not considered; and at 
the horizontal site of a gas pipeline (fig. see) is considered.
Materials can be used also for the solution of problems on work of pneumodrives, electric chains and etc.
References
