| 1. | ||
| 2. | ||
| 3. | ||
| 4. | ||
Equivalent Characterizations and Structure Theorem of Right C-wrpp Semigroups
Deju Zhang1, Xiaomin Zhang2, Enxiao Yuan3
1School of Science, Linyi University, Shandong, P. R. China
2School of Logistic, Linyi University, Shandong, P. R. China
3School of Yishui, Linyi University, Shandong, P. R. China
Email address
 (Deju Zhang)
(Deju Zhang)  (Xiaomin Zhang)
(Xiaomin Zhang)  (Enxiao Yuan)
(Enxiao Yuan) Citation
Deju Zhang, Xiaomin Zhang, Enxiao Yuan. Equivalent Characterizations and Structure Theorem of Right C-wrpp Semigroups. American Journal of Mathematical and Computational Sciences. Vol. 1, No. 1, 2016, pp. 55-61.
Abstract
The aim of this paper is to study the right dual of left C-wrpp semigroup, that is, the strongly wrpp semigroup whose set of idempotents forms a right regular band and the relation ![]() is a congruence. We call this kind of strongly wrpp semigroups right C-wrpp semigroups. This paper generalizes results of right C-rpp semigroups. Some properties and characterizations of right C-wrpp semigroups are investigated.
is a congruence. We call this kind of strongly wrpp semigroups right C-wrpp semigroups. This paper generalizes results of right C-rpp semigroups. Some properties and characterizations of right C-wrpp semigroups are investigated.
Keywords
Right C-wrpp Semigroup, Right Regular Band, Strongly Wrpp Semigroup
1. Introduction
A semigroup ![]() is an rpp semigroup if all of its principal right ideals
is an rpp semigroup if all of its principal right ideals ![]() regarded as right
regarded as right ![]() -systems, are projective (see [3]-[5]). These classes of semigroups and its special subclasses have been studied by Fountain. He also defined a generalized Green’s relation
-systems, are projective (see [3]-[5]). These classes of semigroups and its special subclasses have been studied by Fountain. He also defined a generalized Green’s relation ![]() on a semigroup
on a semigroup ![]() by
by ![]() if and only if the elements
if and only if the elements ![]() of
of ![]() are related by the Green’s relation
are related by the Green’s relation ![]() in some oversemigroup of
in some oversemigroup of ![]() in [5]. In particular, if
in [5]. In particular, if ![]() for some idempotent elements
for some idempotent elements ![]() , then
, then ![]() . Next, he showed that a monoid
. Next, he showed that a monoid ![]() is rpp if and only if each
is rpp if and only if each ![]() -class of
-class of ![]() contains an idempotent. Thus, a semigroup
contains an idempotent. Thus, a semigroup ![]() is an rpp semigroup if each
is an rpp semigroup if each ![]() -class of
-class of ![]() contains at least one idempotent. An rpp semigroup having all of its idempotents lying in its center is called a C-rpp semigroup. It is well known that a semigroup
contains at least one idempotent. An rpp semigroup having all of its idempotents lying in its center is called a C-rpp semigroup. It is well known that a semigroup ![]() is a C-rpp semigroup if and only if
is a C-rpp semigroup if and only if ![]() is a strongly semilattice of left cancellative monoids. Thus, C-rpp semigroups are natural generalizations of Clifford semigroups.
is a strongly semilattice of left cancellative monoids. Thus, C-rpp semigroups are natural generalizations of Clifford semigroups.
For rpp semigroups, the concept of strongly rpp semigroups was first introduced by Guo-Shum-Zhu, that is, an rpp semigroup in which each ![]() contains a unique idempotent
contains a unique idempotent ![]() such that
such that ![]() , where
, where ![]() is set of idempotents of
is set of idempotents of ![]() . Strongly rpp semigroups and their special cases have been extensively studied by many authors (see [6]-[10], [14]-[17]). In particular, we call a strongly rpp semigroup
. Strongly rpp semigroups and their special cases have been extensively studied by many authors (see [6]-[10], [14]-[17]). In particular, we call a strongly rpp semigroup ![]() left C-rpp semigroup if
left C-rpp semigroup if ![]() is a congruence and
is a congruence and ![]() for all
for all ![]() . For such semigroups, Guo has proved that an rpp semigroup is a left C-rpp semigroup if and only if
. For such semigroups, Guo has proved that an rpp semigroup is a left C-rpp semigroup if and only if ![]() is a semilattce of direct products of left cancellative monoids and left zero bands. Thus, a left C-rpp semigroup is clearly a generalized C-rpp semigroup and left C-semigroup.
is a semilattce of direct products of left cancellative monoids and left zero bands. Thus, a left C-rpp semigroup is clearly a generalized C-rpp semigroup and left C-semigroup.
On the other hand, we call a strongly an rpp semigroup ![]() a right C-rpp semigroup if
a right C-rpp semigroup if ![]() is a congruence and
is a congruence and ![]() for all
for all ![]() . It was observed that the concept of right C-rpp semigroups is not a dual of left C-rpp semigroups by Guo [9]. The structure of right C-rpp semigroups has been recently described by Shum and Ren in [17]. It is noteworthy that many properties of left C-rpp semigroups are not dual to those of right C-rpp semigroups (see [9], [17]).
. It was observed that the concept of right C-rpp semigroups is not a dual of left C-rpp semigroups by Guo [9]. The structure of right C-rpp semigroups has been recently described by Shum and Ren in [17]. It is noteworthy that many properties of left C-rpp semigroups are not dual to those of right C-rpp semigroups (see [9], [17]).
Tang [18] has introduced a new set of Green’s two stars relations on a semigroup ![]() by modifying Green’s one star relations on semigroups. Let
by modifying Green’s one star relations on semigroups. Let ![]() be a Green’s relation on a semigroup
be a Green’s relation on a semigroup ![]() . A relation
. A relation ![]() on
on ![]() by: for some
by: for some ![]() ,
,![]() if and only if
if and only if ![]() for all
for all ![]() . In view of this new Green’s two stars relation, he defined the concept of wrpp semigroups, that is, a wrpp semigroup in which each
. In view of this new Green’s two stars relation, he defined the concept of wrpp semigroups, that is, a wrpp semigroup in which each ![]() -class contains at least one idempotent. A wrpp semigroup is a C-wrpp semigroup if all the idempotents of
-class contains at least one idempotent. A wrpp semigroup is a C-wrpp semigroup if all the idempotents of ![]() are central. We have known that a C-wrpp semigroup can be expressed as a strongly semilattice of left
are central. We have known that a C-wrpp semigroup can be expressed as a strongly semilattice of left ![]() -cancellative monoids. Recently, C-wrpp semigroups have been extended to left C-wrpp semigroups by Du-Shum [2]. A wrpp semigroups
-cancellative monoids. Recently, C-wrpp semigroups have been extended to left C-wrpp semigroups by Du-Shum [2]. A wrpp semigroups ![]() is called a left C-wrpp semigroup if
is called a left C-wrpp semigroup if ![]() satisfies the following conditions: (i)for all
satisfies the following conditions: (i)for all ![]() where
where ![]() is set of idempotents in
is set of idempotents in ![]() ; (ii)for all
; (ii)for all ![]() , there exists a unique idempotent
, there exists a unique idempotent ![]() satisfying
satisfying ![]() and
and ![]() ; (iii) for all
; (iii) for all ![]() ,
, ![]() , where
, where ![]() is the smallest left **-ideal of
is the smallest left **-ideal of ![]() generated by
generated by ![]() . if the condition (i) only holds, then
. if the condition (i) only holds, then ![]() is called quasi strong wrpp semigroup, if conditions (i) and (ii) hold, then
is called quasi strong wrpp semigroup, if conditions (i) and (ii) hold, then ![]() is called strong wrpp semigroup. For left C-wrpp semigroups, Du-Shum [3] have obtained a description of curler structure. In fact, left C-wrpp semigroups are indeed a common generalizations on left C-semigroups and left C-rpp semigroups.
is called strong wrpp semigroup. For left C-wrpp semigroups, Du-Shum [3] have obtained a description of curler structure. In fact, left C-wrpp semigroups are indeed a common generalizations on left C-semigroups and left C-rpp semigroups.
Naturally, one would ask whether we can describe the kind of wrpp semigroup as an analogy of right C-rpp semigroups. In this paper, we generalize right C-rpp semigroups to right C-wrpp semigroups. We first introduce the concept of right C-wrpp semigroups, and some properties on right C-wrpp semigroups are given. We shall show that a right C-wrpp semigroup can be described as a semilattice of the direct product of left-![]() cancellative monoids and left zero bands, but the task is not simple as we need to consider the semilattice congruence on abundant wrpp semigroups. Anyway, our results clearly further generalizes both results of Shum-Ren on right C-rpp semigroups and Guo on a notes on right dual of left C-rpp semigroups. Last, the characterizations of a C-wrpp semigroup are given.
cancellative monoids and left zero bands, but the task is not simple as we need to consider the semilattice congruence on abundant wrpp semigroups. Anyway, our results clearly further generalizes both results of Shum-Ren on right C-rpp semigroups and Guo on a notes on right dual of left C-rpp semigroups. Last, the characterizations of a C-wrpp semigroup are given.
For the notations and terminology not given in this paper, the reader is referred to [2], [13], [18].
2. Basic Definitions and Results
We first introduce some definitions and results that are useful in the sequel.
In order to describe wrpp semigroups, Du-Shum introduced the following (+)-Green’s relations. For elements ![]() in a semigroup
in a semigroup ![]() , we define:
, we define:
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
where ![]() is the smallest ideal of
is the smallest ideal of ![]() containing
containing ![]() such that
such that ![]() is the union of some
is the union of some ![]() -classes or some
-classes or some ![]() -classes. For the sake of simplicity, we denote the
-classes. For the sake of simplicity, we denote the ![]() -class (resp.,
-class (resp.,![]() -class,
-class,![]() -class,
-class,![]() -class and
-class and ![]() -class) of
-class) of ![]() containing
containing ![]() by
by ![]() (resp.,
(resp.,![]() and
and ![]() ). The Green’s "egg box" diagram for Green’s relation still holds for these Green’s (+) relations. We have
). The Green’s "egg box" diagram for Green’s relation still holds for these Green’s (+) relations. We have
Lemma 1 [2] The equalities ![]() and
and ![]() hold on a semigroup.
hold on a semigroup.
On the other hand, the Green’s (+) relations on ![]() are also similar to the Green’s relations on
are also similar to the Green’s relations on ![]() , for instance, we have
, for instance, we have ![]() . Moreover, we have the following lemma:
. Moreover, we have the following lemma:
Lemma 2 [2] Let ![]() be a semigroup,
be a semigroup, ![]() . Then
. Then ![]() if and only if there exists
if and only if there exists ![]() with
with ![]() and
and ![]() such that
such that ![]() for all
for all ![]() .
.
A ![]() -class may contain more than one regular
-class may contain more than one regular ![]() -class. This is because if
-class. This is because if ![]() for some idempotent
for some idempotent ![]() and
and ![]() , then the relation
, then the relation ![]() need not always hold. For example, if
need not always hold. For example, if ![]() is a Rees matrix semigroup over a group
is a Rees matrix semigroup over a group ![]() with
with ![]() , then it is not difficult to see that
, then it is not difficult to see that ![]() is an
is an ![]() -simple semigroup containing
-simple semigroup containing ![]() regular
regular ![]() -classes. But if
-classes. But if ![]() is a quasi strongly wrpp semigroup, then we have
is a quasi strongly wrpp semigroup, then we have
Lemma 3 Let ![]() be a quasi strongly wrpp semigroup and
be a quasi strongly wrpp semigroup and ![]() . Then
. Then ![]() if and only if
if and only if ![]() .
.
Proof Necessity. We only need verify that ![]() . If
. If ![]() , then
, then ![]() . By the quasi strong wrpp property of
. By the quasi strong wrpp property of ![]() , we have
, we have ![]() , so
, so ![]() . Thus
. Thus ![]() .
.
Sufficiency. It is clear and we omit the proof.
Lemma 4 Let ![]() be a quasi strongly wrpp semigroup. Then each
be a quasi strongly wrpp semigroup. Then each ![]() -class contains at most one regular
-class contains at most one regular ![]() -class.
-class.
Proof According to Lemma 1, we have ![]() . Let
. Let ![]() If
If ![]() then there exists
then there exists ![]() such that
such that ![]() . By regularity of
. By regularity of ![]() , we obtain that
, we obtain that ![]() is a regular element of
is a regular element of ![]() . According to Lemma 3, we know that
. According to Lemma 3, we know that ![]() . Hence
. Hence ![]() , so
, so ![]() .
.
Definiton 1 A wrpp semigroup ![]() is called a right C-wrpp semigroup, if
is called a right C-wrpp semigroup, if ![]() satisfies the following conditions:
satisfies the following conditions:
(1). ![]() is a quasi strong wrpp semigroup;
is a quasi strong wrpp semigroup;
(2). ![]() is a congruence on
is a congruence on ![]() ;
;
(3). ![]() .
.
We call a band a right regular band if it satisfies the identity ![]() . We now cite the following lemma:
. We now cite the following lemma:
Lemma 5 [15] The following statements are equivalent on a band ![]() :
:
(1). ![]() is a right regular band;
is a right regular band;
(2). ![]() is a congruence;
is a congruence;
(3). ![]() is a semilattice of right zero bands.
is a semilattice of right zero bands.
An immediate result of this lemma is:
Corollary 1 If ![]() is a right regular band, then each
is a right regular band, then each ![]() -class of
-class of ![]() contains precisely one idempotent.
contains precisely one idempotent.
3. Characterizations of Right C-wrpp Semigroups
In this section, we shall describe some characterizations of right C-wrpp semigroups and hence generalize the main results of right C-rpp semigroups obtained by Guo in [9]. The results obtained in [9] will be amplified and strengthened.
Lemma 6 Let ![]() be a right C-wrpp semigroup. Then the following hold:
be a right C-wrpp semigroup. Then the following hold:
(1). ![]() is a right regular band;
is a right regular band;
(2). Reg![]() is a right C-semigroup.
is a right C-semigroup.
Proof (1) Let ![]() . Since
. Since ![]() , then there exists
, then there exists ![]() such that
such that ![]() , so
, so ![]() . Hence
. Hence ![]() , it implies that
, it implies that ![]() is a band and a right regular band.
is a band and a right regular band.
(2) According to (1), ![]() is a band, so Reg
is a band, so Reg![]() is a regular subsemigroup of
is a regular subsemigroup of ![]() . And for all
. And for all ![]() , (Reg
, (Reg![]() Reg
Reg![]() Reg
Reg![]() ), consequently, Reg
), consequently, Reg![]() is a right C-semigroup (see [20]).
is a right C-semigroup (see [20]).
Theorem 1 The following statements are equivalent:
(1). ![]() is a right C-wrpp semigroup;
is a right C-wrpp semigroup;
(2). ![]() is a strong wrpp semigroup such that
is a strong wrpp semigroup such that ![]() is a semilattice congruence, and
is a semilattice congruence, and ![]() ;
;
(3). ![]() is a semilattice of
is a semilattice of ![]() -simple strong wrpp semigroups, and
-simple strong wrpp semigroups, and ![]() ;
;
(4). ![]() is a semilattice of
is a semilattice of ![]() for
for ![]() , where
, where ![]() is a left
is a left![]() cancellative monoid,
cancellative monoid, ![]() is a right zero band.
is a right zero band.
Proof (1)![]() (2). Let
(2). Let ![]() be a right wrpp semigroup. Then
be a right wrpp semigroup. Then ![]() is a congruence of
is a congruence of ![]() . Let
. Let ![]() , and
, and ![]() . Then clearly
. Then clearly ![]() . But
. But ![]() is a congruence, we have
is a congruence, we have ![]() , so
, so ![]() . Notice that
. Notice that ![]() is a right regular band, it leads to
is a right regular band, it leads to ![]()
![]() Consequently,
Consequently, ![]() is a semilattice congruence.
is a semilattice congruence.
According to Lemma 6, Reg![]() is a right C-semigroup. Therefore, Reg
is a right C-semigroup. Therefore, Reg![]() /
/![]() is a semilattice, and
is a semilattice, and ![]() by Lemma 6, We easily prove that
by Lemma 6, We easily prove that ![]() . By quasi wrpp property of
. By quasi wrpp property of ![]() , and Lemma 4, we know that each
, and Lemma 4, we know that each ![]() -class exactly contains one regular
-class exactly contains one regular ![]() -class, and each
-class, and each ![]() -class exactly contains one regular
-class exactly contains one regular ![]() -class, it means that each
-class, it means that each ![]() -class in each
-class in each ![]() -class contains a unique idempotent which is a left identity of this
-class contains a unique idempotent which is a left identity of this ![]() -class. Again,
-class. Again, ![]() for all
for all ![]() , so this unique idempotent is also a right identity of above
, so this unique idempotent is also a right identity of above ![]() -class. Hence
-class. Hence ![]() is a strongly wrpp semigroup.
is a strongly wrpp semigroup.
(2)![]() (3). Let
(3). Let ![]() be a semilattice decomposition corresponding to the semilattice congruence
be a semilattice decomposition corresponding to the semilattice congruence ![]() . Obviously, for an arbitrary subsemigroup
. Obviously, for an arbitrary subsemigroup ![]() of
of ![]() , we have
, we have ![]() . Hence the elements of
. Hence the elements of ![]() having
having ![]() relation in
relation in ![]() also have
also have ![]() relation in
relation in ![]() . By
. By ![]() , and Lemma 4, it implies that each
, and Lemma 4, it implies that each ![]() only contains one regular
only contains one regular ![]() -class. Therefore, the elements of
-class. Therefore, the elements of ![]() having
having ![]() relation in
relation in ![]() and also have
and also have ![]() relation in
relation in ![]() , so each
, so each ![]() -class
-class ![]() is
is ![]() -simple, and is a strongly wrpp semigroup.
-simple, and is a strongly wrpp semigroup.
(3)![]() (4). Let
(4). Let ![]() be a semilattice decomposition
be a semilattice decomposition ![]() , where
, where ![]() is a
is a ![]() -simple strong wrpp semigroup. Let
-simple strong wrpp semigroup. Let ![]() . According to
. According to ![]() , we know that each
, we know that each ![]() -class
-class ![]() of
of ![]() contains a unique idempotent
contains a unique idempotent ![]() , and
, and ![]() is a right zero band. Next we shall verify that
is a right zero band. Next we shall verify that ![]() . Let
. Let ![]() . Then
. Then ![]() , so
, so ![]() . Since
. Since ![]() , it leads to
, it leads to ![]() . Hence
. Hence ![]() , so
, so ![]() . Conversely, if
. Conversely, if ![]() (
(![]() ), then
), then ![]() , and
, and ![]() , it is easily observed that
, it is easily observed that ![]() , it means
, it means ![]() . Thus
. Thus ![]() . By strong wrpp property of
. By strong wrpp property of ![]() , we have
, we have ![]() , which is a monoid with identity element
, which is a monoid with identity element ![]() for all
for all ![]() . We claim that
. We claim that ![]() is left-
is left-![]() cancellative. In fact, for all
cancellative. In fact, for all ![]() , if
, if ![]() , notice that
, notice that ![]() , then
, then ![]() . Now define a mapping:
. Now define a mapping:
![]() (5)
(5)
for any fixed ![]() . Then we deduce that
. Then we deduce that ![]()
![]() . Thus,
. Thus, ![]() is a semigroup homomorphism.
is a semigroup homomorphism.
We now show that ![]() is a semigroup isomorphism. By virtue of the strongly wrpp property of
is a semigroup isomorphism. By virtue of the strongly wrpp property of ![]() , for all
, for all ![]() , there exists
, there exists ![]() such that
such that ![]() . By the definition of
. By the definition of ![]() , this means that
, this means that ![]() , and hence
, and hence ![]() is an epimorphism. To prove
is an epimorphism. To prove ![]() is a monomorphism, we assume that
is a monomorphism, we assume that ![]() . Then we have
. Then we have ![]() Since
Since ![]() is a right zero band, we have
is a right zero band, we have ![]() . This implies that
. This implies that ![]() for all
for all ![]() . Invoking the strongly wrpp property of
. Invoking the strongly wrpp property of ![]() , we obtain that
, we obtain that ![]() This shows that
This shows that ![]() is a monomorphism as well. Thus
is a monomorphism as well. Thus ![]() . The proof is completed.
. The proof is completed.
1em (4)![]() (1). Let
(1). Let ![]() is a semilattice of
is a semilattice of ![]() for
for ![]() , where
, where ![]() is a left-
is a left-![]() cancellative monoid,
cancellative monoid, ![]() is a right zero band. Then
is a right zero band. Then ![]() , where
, where ![]() is unique identity of left-
is unique identity of left-![]() monoid
monoid ![]() . We now show that
. We now show that ![]() is a
is a ![]() -class. Let
-class. Let ![]() , and
, and ![]() . Then there exists
. Then there exists ![]() such that
such that ![]() . Since
. Since ![]() if and only if
if and only if ![]() , so
, so ![]() . Hence we have
. Hence we have ![]() for any
for any ![]() , it implies that
, it implies that ![]() . This means that
. This means that ![]() . Similarly, we can verify that
. Similarly, we can verify that ![]() . Hence we conclude that
. Hence we conclude that ![]() . Because
. Because ![]() is just a
is just a ![]() -class of
-class of ![]() ,
, ![]() must be a semilattice congruence on
must be a semilattice congruence on ![]() .
.
1emNext, we need verify that ![]() . Let
. Let ![]() and
and ![]() with
with ![]() . Then
. Then ![]() . In fact,
. In fact, ![]()
![]() , then
, then ![]() , so
, so
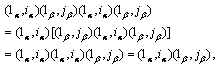
that is,![]() Clearly,
Clearly, ![]() , by using above analogous methods, we obtain that
, by using above analogous methods, we obtain that ![]()
![]() for any
for any ![]() . Hence, we have
. Hence, we have
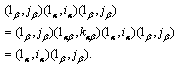
This means that ![]() is a right regular band. Now let
is a right regular band. Now let ![]() , then
, then
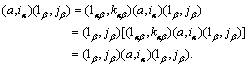
This verifies that ![]() .
.
Summing up the above results, then ![]() is a right C-wrpp semigroup.
is a right C-wrpp semigroup.
Corollary 2 Let ![]() is a right C-wrpp semigroup. Then
is a right C-wrpp semigroup. Then ![]() .
.
Proof Because ![]() , we only need to prove that
, we only need to prove that ![]() . Suppose that
. Suppose that ![]() . Then
. Then ![]() . By Lemma 2, there exists
. By Lemma 2, there exists ![]() with
with ![]() and
and ![]() such that
such that ![]() for all
for all ![]() Since
Since ![]() and
and ![]() is a congruence, we have
is a congruence, we have![]()
![]() . By Theorem 1, we know that
. By Theorem 1, we know that ![]() is a semilattice congruence. We denote semilattice
is a semilattice congruence. We denote semilattice ![]() by
by ![]() . Index
. Index ![]() -class in virtue of the elements
-class in virtue of the elements ![]() in the semilattice
in the semilattice ![]() , and let
, and let ![]() . We are not difficult to see that
. We are not difficult to see that ![]() . Similarly,
. Similarly, ![]() . Hence
. Hence ![]() .
.
Lemma 7 Let ![]() be a strongly wrpp semigroup whose set of idempotents is a semilattice
be a strongly wrpp semigroup whose set of idempotents is a semilattice ![]() . Then
. Then ![]() for all
for all ![]() .
.
Lemma 8 Let ![]() be a strongly wrpp semigroup whose set of idempotents is a semilattice
be a strongly wrpp semigroup whose set of idempotents is a semilattice ![]() , and
, and ![]() . If
. If ![]() , then the following statements are hold:
, then the following statements are hold:
(1). ![]() is a left-
is a left-![]() cancellative monoid;
cancellative monoid;
(2). If ![]() , and
, and ![]() , then the mapping
, then the mapping ![]() :
:
![]() (6)
(6)
is a semigroup homomorphism. Moreover, with respect to the following multiplication "![]() ":
":
![]() (7)
(7)
![]() form a C-wrpp semigroup, where
form a C-wrpp semigroup, where ![]() is the product in
is the product in ![]() ;
;
(3). ![]() , where
, where ![]() is the product of
is the product of ![]() and
and ![]() in
in ![]() .
.
Proof (1) Let ![]() . Notice that there is exactly one idempotent in
. Notice that there is exactly one idempotent in ![]() , we have
, we have ![]() . By the fact that
. By the fact that ![]() being a strongly wrpp semigroup, we have
being a strongly wrpp semigroup, we have ![]() . Since
. Since ![]() is a right congruence, we know that
is a right congruence, we know that ![]() . Hence
. Hence ![]() is a subsemigroup of
is a subsemigroup of ![]() . Notice that
. Notice that ![]() , it follows that
, it follows that ![]() is the identity of
is the identity of ![]() . Now put
. Now put ![]() , and
, and ![]() . Then
. Then ![]() . Thus
. Thus ![]() , that is,
, that is, ![]() is a left-
is a left-![]() cancellative monoid.
cancellative monoid.
(2) Let ![]() . Since
. Since ![]() is a right congruence, we have
is a right congruence, we have ![]() , that is,
, that is, ![]() . By (1), we know that
. By (1), we know that ![]() is a left-
is a left-![]() cancellative monoid with identity
cancellative monoid with identity ![]() . Consequently, for all
. Consequently, for all ![]() , we have
, we have
![]() (8)
(8)
Thus ![]() is a semigroup homomorphism. It is not difficult to verify that
is a semigroup homomorphism. It is not difficult to verify that ![]() is a strongly semilattice structure homomorphism on
is a strongly semilattice structure homomorphism on ![]() . Therefore,
. Therefore, ![]() is a C-wrpp semigroup.
is a C-wrpp semigroup.
(3) Since ![]() is a right congruence, we have
is a right congruence, we have ![]() . By Lemma 7, we obtain that
. By Lemma 7, we obtain that ![]() . It means that
. It means that ![]() . Because
. Because ![]() is the identity of
is the identity of ![]() , we have
, we have
![]() (9)
(9)
Lemma 9 Let ![]() be a semigroup satisfying the conditions in Lemma 8. Then every regular element of
be a semigroup satisfying the conditions in Lemma 8. Then every regular element of ![]() is completely regular, that is, a regular element is
is completely regular, that is, a regular element is ![]() -related to an idempotent element.
-related to an idempotent element.
Proof Let ![]() be a regular element of
be a regular element of ![]() . Then there exists
. Then there exists ![]() such that
such that ![]() , so
, so ![]() . Hence
. Hence ![]() . As it is argued in Lemma 3.5,
. As it is argued in Lemma 3.5, ![]() . Hence
. Hence ![]() is a regular element of
is a regular element of ![]() and
and ![]() is an idempotent of
is an idempotent of ![]() . But there is only one idempotent in
. But there is only one idempotent in ![]() , so
, so ![]() . Thus
. Thus ![]() , that is,
, that is, ![]() is a completely regular element.
is a completely regular element.
Lemma 10 Let ![]() be a strongly semigroup whose set of idempotents is a band. Then every regular element of
be a strongly semigroup whose set of idempotents is a band. Then every regular element of ![]() is a completely regular element
is a completely regular element
Proof Since ![]() is a band, Reg
is a band, Reg![]() is a orthodox semigroups. Since
is a orthodox semigroups. Since ![]() is a strongly wrpp semigroup, we can easily see that Reg
is a strongly wrpp semigroup, we can easily see that Reg![]() is a strongly wrpp semigroup. Hence Reg
is a strongly wrpp semigroup. Hence Reg ![]() is a strongly wrpp semigroup, where
is a strongly wrpp semigroup, where ![]() is the smallest inverse semigroup congruence on Reg
is the smallest inverse semigroup congruence on Reg![]() . According to Lemma 9, we can follow that Reg
. According to Lemma 9, we can follow that Reg ![]() is a Clofford semigroup. Let
is a Clofford semigroup. Let ![]() . Then there exists
. Then there exists ![]() such that
such that ![]() . It follows that
. It follows that ![]() . By Reg
. By Reg![]() being a Clifford semigroup,
being a Clifford semigroup, ![]() . On the other hand, since
. On the other hand, since ![]() , we have
, we have ![]() and hence
and hence ![]() . Therefore
. Therefore ![]() , that is,
, that is, ![]() is a completely regular element.
is a completely regular element.
As an application of above results, we now give some conditions which lead to a C-wrpp semigroup ![]() for some congruence
for some congruence ![]() defined on a right C-wrpp semigroup
defined on a right C-wrpp semigroup ![]() . In fact, all we need to find a congruence
. In fact, all we need to find a congruence ![]() on
on ![]() so that
so that ![]() preserves the
preserves the ![]() -classes of
-classes of ![]() .
.
For convenience, we denote the rectangular band ![]() by
by ![]() if the idempotent
if the idempotent ![]() is in
is in ![]() . Also, we write
. Also, we write ![]() if
if ![]() .
.
We now characterize right C-wrpp semigroups.
Theorem 2 The following conditions are equivalent for a strongly wrpp semigroup ![]() :
:
(1). ![]() is a right C-wrpp semigroup;
is a right C-wrpp semigroup;
(2). ![]() is a right regular band and
is a right regular band and ![]() is a semilattice congruence on
is a semilattice congruence on ![]() ;
;
(3). The relation ![]() is a congruence on
is a congruence on ![]() such that
such that ![]() is a C-wrpp semigroup.
is a C-wrpp semigroup.
Proof (1)![]() (2). This part is an immediate consequence of Lemma 6 and Theorem 1.
(2). This part is an immediate consequence of Lemma 6 and Theorem 1.
(2)![]() (1). Let
(1). Let ![]() be a right regular band and suppose that
be a right regular band and suppose that ![]() is a congruence on
is a congruence on ![]() . To show that
. To show that ![]() is a right C-wrpp semigroup, we only need to verify that
is a right C-wrpp semigroup, we only need to verify that ![]() . By Lemma 5, we have
. By Lemma 5, we have ![]() . On the other hand, for all
. On the other hand, for all ![]() with
with ![]() , by Lemma 10, there exists
, by Lemma 10, there exists ![]() such that
such that ![]() . Clearly,
. Clearly, ![]() , and then there exists some
, and then there exists some ![]() such that
such that ![]() . Again by Lemma 10, there exists
. Again by Lemma 10, there exists ![]() such that
such that ![]() . Thus,
. Thus, ![]() , that is,
, that is, ![]() . Consequently,
. Consequently, ![]() and
and ![]() . Thus, we have proved that
. Thus, we have proved that ![]() . The proof is completed.
. The proof is completed.
(2)![]() (3). We can assume that
(3). We can assume that ![]() is a right C-wrpp semigroup. Then we have
is a right C-wrpp semigroup. Then we have ![]() for every
for every ![]() and because
and because ![]() is a strongly wrpp semigroup,
is a strongly wrpp semigroup, ![]() for
for ![]() . Thus,
. Thus, ![]() . This means that
. This means that ![]() is reflexive. To see that
is reflexive. To see that ![]() is symmetric, we let
is symmetric, we let ![]() . Then, by the definition of
. Then, by the definition of ![]() , we have
, we have ![]() for
for ![]() . Since
. Since ![]() , we also have
, we also have ![]() . Consequently, we get
. Consequently, we get ![]() and
and ![]() . Thus
. Thus ![]() . From
. From ![]() , we immediately get
, we immediately get ![]() . This shows that
. This shows that ![]() is symmetric. To see that
is symmetric. To see that ![]() is transitive, we let
is transitive, we let ![]() and
and ![]() . Then there exists
. Then there exists ![]() such that
such that ![]() . By repeating the arguments given above, we have
. By repeating the arguments given above, we have ![]() . This leads to
. This leads to ![]() . By
. By ![]() , we have
, we have ![]() . Hence
. Hence ![]() is indeed an equivalent relation on
is indeed an equivalent relation on ![]() .
.
1emTo see that ![]() is a congruence on
is a congruence on ![]() , we let
, we let ![]() . Then, by the definition of
. Then, by the definition of ![]() , there exists
, there exists ![]() such that
such that ![]() . Hence
. Hence ![]() . By invoking Theorem 1 (4), we have
. By invoking Theorem 1 (4), we have ![]() , that is,
, that is, ![]() . This leads to
. This leads to ![]() . In other words, we have
. In other words, we have ![]() and hence
and hence ![]() is left compatible. Similarly, we can verify that
is left compatible. Similarly, we can verify that ![]() is right compatible. Thus
is right compatible. Thus ![]() is indeed a congruence on
is indeed a congruence on ![]() .
.
We still need to show that ![]() preserve the
preserve the ![]() -classes of
-classes of ![]() . For this purpose, we let
. For this purpose, we let ![]() for some
for some ![]() . If there are
. If there are ![]() such that
such that ![]() , then there exists
, then there exists ![]() such that
such that ![]() and
and ![]() . Hence, we can find
. Hence, we can find ![]() such that
such that ![]() . By
. By ![]() being a semilattice congruence, we can deduce that
being a semilattice congruence, we can deduce that ![]() and similarly,
and similarly,![]() . This leads to
. This leads to ![]() . Clearly,
. Clearly, ![]() and consequently,
and consequently, ![]() and
and ![]() , that is,
, that is, ![]() . So we also have
. So we also have ![]() . Therefore, by the definition of
. Therefore, by the definition of ![]() , there exists
, there exists ![]() such that
such that ![]() and
and ![]() . On the other hand, since
. On the other hand, since ![]() , we have
, we have ![]() and hence we deduce that
and hence we deduce that ![]() . Similarly,
. Similarly,![]() .
.
Since ![]() , we have
, we have ![]() and hence
and hence ![]() This leads to
This leads to ![]() . Similarly,
. Similarly, ![]() . Thus, we have
. Thus, we have ![]() . From this relation and its dual, we conclude that
. From this relation and its dual, we conclude that ![]() This shows that the relation
This shows that the relation ![]() on
on ![]() is preserved in the quotient semigroup
is preserved in the quotient semigroup ![]() , and hence
, and hence ![]() is a wrpp semigroup.
is a wrpp semigroup.
Finally, we show that the idempotents of ![]() are central. It suffices to show that
are central. It suffices to show that ![]() for all
for all ![]() and
and ![]() . Since by Theorem 1 (4),
. Since by Theorem 1 (4), ![]() , it is clear that
, it is clear that ![]() . Thus, by
. Thus, by ![]() , we obtain that
, we obtain that ![]() . This shows that
. This shows that ![]() is a C-wrpp semigroup.
is a C-wrpp semigroup.
(3)![]() (1). Suppose that
(1). Suppose that ![]() is a congruence on
is a congruence on ![]() such that
such that ![]() is a C-wrpp semigroup. we can easily see that
is a C-wrpp semigroup. we can easily see that ![]() and hence
and hence ![]() is a semilattice. Hence
is a semilattice. Hence ![]() is a semilattice congruence on
is a semilattice congruence on ![]() , and so
, and so ![]() is a right regular band. Now let
is a right regular band. Now let ![]() be the semilattcie decomposition of
be the semilattcie decomposition of ![]() into right zero bands
into right zero bands ![]() . Clearly,
. Clearly, ![]() is isomorphic to
is isomorphic to ![]() . We identify
. We identify ![]() with
with ![]() . By
. By ![]() is a C-wrpp semigroup, we let
is a C-wrpp semigroup, we let ![]() be the semilattice decomposition of the C-wrpp semigroup
be the semilattice decomposition of the C-wrpp semigroup ![]() into left-
into left-![]() cancellative monoids
cancellative monoids ![]() .
.
Put ![]() . Then we define
. Then we define ![]() by
by ![]() . Clearly,
. Clearly, ![]() is well defined, and we deduce that
is well defined, and we deduce that
![]() . (10)
. (10)
Thus ![]() is a semigroup homomorphism.
is a semigroup homomorphism.
Now we prove that ![]() is a semigroup isomorphism. For all
is a semigroup isomorphism. For all ![]() , we have
, we have ![]() such that
such that ![]() and
and ![]() . It follows that
. It follows that ![]() . On the other hand, since
. On the other hand, since ![]() , we have
, we have ![]() . But
. But ![]() is a right regular band, we know that each
is a right regular band, we know that each ![]() -class of
-class of ![]() contains precisely one element, and thus
contains precisely one element, and thus ![]() . Consequently,
. Consequently, ![]() . This means that
. This means that ![]() is an epimorphism. To prove
is an epimorphism. To prove ![]() is a monomorphism, now let
is a monomorphism, now let ![]() and
and ![]() . Then
. Then ![]() and
and ![]() . By using the latter formula, we see that there exists
. By using the latter formula, we see that there exists ![]() such that
such that ![]() , and furthermore,
, and furthermore, ![]() . This shows that
. This shows that ![]() is also a monomorphism. On the other hand,
is also a monomorphism. On the other hand, ![]() is a semilattice of direct products
is a semilattice of direct products ![]() and hence
and hence ![]() is a right C-wrpp semigroup.
is a right C-wrpp semigroup.
Now we define a new relation ![]() on a strongly wrpp
on a strongly wrpp ![]() as follows:
as follows:
![]() (11)
(11)
It is easy to verify that ![]() is a equivalent relation, and
is a equivalent relation, and ![]()
Theorem 3 Let ![]() be a strongly wrpp semigroup. Then
be a strongly wrpp semigroup. Then ![]() is a right C-wrpp semigroup if and only if
is a right C-wrpp semigroup if and only if ![]() is a semilattice congruence
is a semilattice congruence ![]() and
and ![]() is a right regular band.
is a right regular band.
Proof Assume that ![]() is a right C-wrpp semigroup. By Lemma 6 (1), we only need to prove that
is a right C-wrpp semigroup. By Lemma 6 (1), we only need to prove that ![]() is a semilattice congruence. For this purpose, we let
is a semilattice congruence. For this purpose, we let ![]() is a semilattice of the direct products
is a semilattice of the direct products ![]() for
for ![]() , where
, where ![]() is a left-
is a left-![]() cancellative monoid and
cancellative monoid and ![]() is a right zero band. We can easily check that
is a right zero band. We can easily check that ![]() for any
for any ![]() , where
, where ![]() is the identity of
is the identity of ![]() . Hence it is difficult to verify that identical formula
. Hence it is difficult to verify that identical formula ![]() . It follows that
. It follows that ![]() is a semilattice congruence.
is a semilattice congruence.
Suppose that ![]() is a semilattice congruence on
is a semilattice congruence on ![]() and
and ![]() is a right regular band. Since
is a right regular band. Since ![]() is a semilattice congruence on
is a semilattice congruence on ![]() ,
, ![]() is a semilattice of some
is a semilattice of some ![]() -classes. But
-classes. But ![]() , each
, each ![]() -class of
-class of ![]() is a strongly wrpp semigroup, therefore it is
is a strongly wrpp semigroup, therefore it is ![]() -simple. Next we shall show that each
-simple. Next we shall show that each ![]() -simple semigroup is also
-simple semigroup is also ![]() -simple semigroup. For this purpose, we only need to prove
-simple semigroup. For this purpose, we only need to prove ![]() . Let
. Let ![]() . Then
. Then ![]() . Hence there exists
. Hence there exists ![]() such that
such that ![]() . By
. By ![]() , we can see that
, we can see that ![]() is a regular element, and by Lemma 10,
is a regular element, and by Lemma 10, ![]() is completely regular. Hence, we can follow that
is completely regular. Hence, we can follow that ![]() . This means that
. This means that ![]() , so
, so ![]() . Conversely, if
. Conversely, if ![]() , then there exist
, then there exist ![]() with
with ![]() such that
such that ![]() .
. ![]() . From the above, we have
. From the above, we have
![]() (12)
(12)
This shows that ![]() . Hence
. Hence ![]() This shows that
This shows that ![]() . Thus, each
. Thus, each ![]() -simple semigroup is also
-simple semigroup is also ![]() -simple semigroup, it deduces that
-simple semigroup, it deduces that ![]() is a semilattice of
is a semilattice of ![]() -simple strongly wrpp semigroups.
-simple strongly wrpp semigroups.
Also, Since ![]() is a right regular band, by the proof of
is a right regular band, by the proof of ![]() in Theorem 2, we know that
in Theorem 2, we know that ![]() . Therefore,
. Therefore, ![]() is a right C-wrpp semigroup.
is a right C-wrpp semigroup.
Theorem 4 Let ![]() be a strongly wrpp semigroup whose set of idempotents forms a right regular band. Then the following statements are equivalent:
be a strongly wrpp semigroup whose set of idempotents forms a right regular band. Then the following statements are equivalent:
(1). ![]() is a right wrpp semigroup;
is a right wrpp semigroup;
(2). ![]() ;
;
(3). ![]() .
.
Proof ![]() . By the Corollary 2, clearly.
. By the Corollary 2, clearly.
![]() . Let
. Let ![]() . Since
. Since ![]() is a right regular band, we have
is a right regular band, we have ![]() (see the proof of Theorem 2). Let
(see the proof of Theorem 2). Let ![]() and
and ![]() . Then
. Then ![]() and hence
and hence ![]() . This leads to
. This leads to ![]() by Lemma 4. Thus
by Lemma 4. Thus ![]() , that is,
, that is, ![]() . Consequently,
. Consequently, ![]() and so
and so ![]() .
.
![]() . Assume that
. Assume that ![]() . By Theorem 4, we only need to verify that
. By Theorem 4, we only need to verify that ![]() is a semilattice congruence on
is a semilattice congruence on ![]() . For this purpose, we prove that
. For this purpose, we prove that ![]() is a semilattice congruence on
is a semilattice congruence on ![]() . Let
. Let ![]() . Since
. Since ![]() is a right congruence, we have
is a right congruence, we have ![]() . Hence
. Hence ![]() , this means that
, this means that ![]() . Thus, for any
. Thus, for any ![]() , we have
, we have ![]() Similarly, we have
Similarly, we have ![]() and so
and so ![]() . Now we let
. Now we let ![]() with
with ![]() . Because
. Because ![]() is a right congruence, we have
is a right congruence, we have ![]() . Similarly,
. Similarly, ![]() . According to
. According to ![]() being a right regular band, we can follow that
being a right regular band, we can follow that ![]() , thus
, thus ![]() . Therefore,
. Therefore, ![]() is a semilattice congruence, that is,
is a semilattice congruence, that is, ![]() is a semilattice congruence. Consequently,
is a semilattice congruence. Consequently, ![]() is a right C-wrpp.
is a right C-wrpp.
4. Conclusions
In this paper, we show that a right C-wrpp semigroup can be described as a semilattice of the direct product of left-![]() cancellative monoids and left zero bands, our results further generalizes both results of Shum-Ren on right C-rpp semigroups and Guo on a notes on right dual of left C-rpp semigroups. Last, the characterizations of a C-wrpp semigroup are given, that is,
cancellative monoids and left zero bands, our results further generalizes both results of Shum-Ren on right C-rpp semigroups and Guo on a notes on right dual of left C-rpp semigroups. Last, the characterizations of a C-wrpp semigroup are given, that is,![]() is a right wrpp semigroup if and only if the relatons
is a right wrpp semigroup if and only if the relatons ![]() or
or ![]() .
.
Acknowledgment
This research is supported by Foundation of Shandong Province Natural Science (Grant No. ZR2010AL004). The author wish to thank the anonymous referee for the comments to improve the presentation and value suggesting.
References