Analysis of Using Z-evaluation Uncertainty in Fuzzy Inference Systems

Primova H. A., Niyozmatova N. A.

Centre for the Development of Software and Hardwarily-Program Complex of Tashkent, University of Information Technologies, Tashkent, Uzbekistan

Email address

Citation

Primova H. A., Niyozmatova N. A. Analysis of Using Z-evaluation Uncertainty in Fuzzy Inference Systems. American Journal of Mathematical and Computational Sciences. Vol. 1, No. 2, 2016, pp. 67-73.

Abstract

This article discusses the construction of a model based on fuzzy inference rules using Z-evaluation, aimed at obtaining conclusions with the use of vague, inaccurate or incomplete initial information. A common approach of computing Z-numbers based on the principle of Zadeh expansion is offered. It outlines the basic arithmetic operations on discrete Z-numbers. We consider three types of fuzzy models for assessing the status of poorly formalized process, the output of which is a linear and non-linear dependence, as well as in the form of fuzzy terms. The computational experiments are done and the results are analyzed.

Keywords

Discrete Z-number, Z-evaluation, Fuzzy Rules, Fuzzy Inference

1. Introduction

In 2011, Professor of the University California (Berkeley) Lotfi Zadeh, the founder of the theory of fuzzy sets, fuzzy logic and computing with words, proposed the concept of Z-number to describe the inaccuracies (proximity) of information used in everyday life. Such information is not entirely accurate; in most cases, people associate varying degrees of confidence when expressing views, describing situations and etc.., depending on their experience, intuition and awareness

The general approach for computing of Z-numbers is proposed in [1] based on the principle of Zadeh expansion. This approach is computationally very complex, it includes several variational problems. To overcome this difficulty, several simplifications are suggested. In general, the work [1] is the beginning, which opens the door to many potential applications of computing Z-numbers and claims several related important issues. In [2] the authors propose an approach for transforming Z-numbers in fuzzy number [3] on the basis of fuzzy expectation of a fuzzy set. Under the proposed approach, with the second component  defuzzification operation is performed to clear the values of alpha, which is then multiplied by . However, it should be noted that the conversion of Z-numbers in the classic fuzzy numbers [4, 5] results in a loss of the original information. In [6], the Z-numbers are applied to the multi-criteria decision-making problems, given in [2]. In this problem, the weighting criteria and the criteria for assessment of alternatives are given in the form of Z-numbers. However, in general, evaluating alternatives are considered as crisp numbers. Papers [7, 8] are devoted to new ideas, approaches and applications of Z-numbers in a variety of important areas. It is proposed to consider the Z-evaluation  in terms of the distribution capabilities of probability distributions underlying the corresponding Z-number . The proposed approach considers only typical distribution. The author also provides an alternative formulation of Z-data in terms of Dempster-Shafer theory [9], which comprises a plurality of fuzzy type-2 [10]. The paper [11] is devoted to the issues of calculation of continuous Z-numbers and some important practical problems in the field of control and decision-making. This research is based on the use of the normal density functions for the simulation of random variables. Among the important issues raised in the paper [11] we can show IF-THEN calculation rules described by Z-numbers.

The paper [12] is devoted to solve the problems in the face of uncertainty, when the relevant information is described by Z-numbers. The authors formulate decision making problem when the probabilities of the states of objects and the results of the alternatives are described by Z-numbers. A decision analysis on the basis of the approach is proposed in [2]. The main disadvantage of the proposed study is a loss of information as a result of the conversion of Z-numbers into fuzzy numbers.

We can conclude that there is no general and computationally efficient approach to computing of Z-numbers. The development of a universal approach for the easy use for a wide range of practical tasks, such as monitoring, analysis, decision-making and optimization [13, 14] is one of the problems of current interest. In turn, this requires the definition of arithmetic on Z-numbers.

2. Formulation of the Problem

We can say that the theory of Z-numbers is not sufficiently investigated yet (most famous publications relates to the period of 2012-2015.), but scientists have already contributed to the development of the theory of Z-numbers and suggested some approaches to dealing with them, which will be considered in this paper. Nevertheless, the use of Z-numbers in the fuzzy system output still remains as an unsolved problem because they are used in the representation of components of different nature.

The purpose of this article is to study the methods of using Z-numbers in fuzzy inference systems and the development of programs based on the results of this study. To achieve this goal the following objectives have been identified:

1.   Study of existing approaches to operations with Z-numbers.

2.   Development of using algorithm of the transformed Z-numbers in the fuzzy output systems.

3.   Study of the possibilities of using Z-numbers in the output system without pre-modification (conversion).

4.   Development of a program that implements the proposed method.

5.   Carrying out the experiments and analysis of the results.

In this paper, we propose an approach based on the use of the transformed Z-numbers (the transition to the normal fuzzy numbers) in the fuzzy system output. The paper also analyzes the arithmetic operations on Z-numbers, which have been formalized at the time of writing operation, the prospects for their use in fuzzy inference systems and formulated the problems that arise in this case.

3. Discrete Z-number

The discrete Z-number is the ordered pair , where  the discrete fuzzy number plays the role of fuzzy constraints on the values that the random variable X can accept [1, 3]:

and  is discrete fuzzy number with a membership function, playing the role of a fuzzy constraints on measures of probability :

The notion of a discrete Z ⁺-number is closely linked with the concept of a discrete Z-number. Given the a discrete Z- number of Z ⁺ is the number Z ⁺ of a pair consisting of the of fuzzy number  and of the random number R [12]:

,

where  plays the same role as in discrete Z- numbers  and R plays a role the probability distribution p, such that

.

Let the  and  continuous Z-number that describes the values of X₁ and X₂ indefinite of real variables. Suppose that it is needed for the calculation . Computation with continuous Z-numbers begins with the computation of the corresponding continuous Z⁺-numbers  and , where in R₁ and R₂ of the probability distribution. Thus, the first need to calculate [13, 16].

For simplicity, consider the case where * is the sum and assume that X₁ and X₂ are independent. As operands  and  presented in the different types of the limitations, the values * also distinguished [16].  defined as

In turn,  is probability density

.

Hence, , where .

Now we realize that the "true" probability distribution  and  are not known. In opposite that,  and  are in the following constraints fuzzy

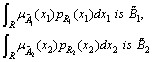
which are represented in terms of membership functions as

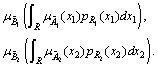
Thus, information  also be presented fuzzy constraint. Problem construction of this fuzzy restriction is formulated

                     (1)

on condition

                                                               (2)

                                                                                  (3)

                                                                                  (4)

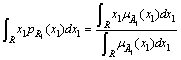 (compatibility condition for)                                           (5)

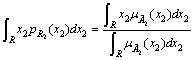 (compatibility condition for)                                         (6)

As you can see, (1) - (6) it is a very complex nonlinear variational problem. More specifically, the problem of constructing membership functions for a variety of package and operands problems of probability density, which are discussed in a general sense. This problem may be simplified if the assumption can impose sufficient to use some typical forms of distribution such as a Gaussian type distribution. However, even in this case, the problem is very complex and of analytical and computational points of view.

As it see, (1) - (6) it is a very complex nonlinear variational problem. More specifically, the problem of constructing membership functions for a variety of package  and operands problems of probability  and  density, which are discussed in a general sense. This problem may be simplified if the assumption can impose sufficient to use some typical forms of distribution such as a Gaussian type distribution. However, even in this case, the problem is very complex and of analytical and computational points of view.

After the construction , we have to go to the final stage of of calculating the required Z-number , ie the definition . This problem is formulated as follows:

on condition

As seen, newly dealing with a nonlinear variational problem. In order to overcome the complexity of operations with continuous Z-numbers, we offer an alternative approach. This approach consists in considering the discrete Z-numbers as discrete analogues of continuous Z-numbers [1, 13].

4. The Theoretical Part

An ordered triple, which is interpreted as an operator (approval) "U is (A, B)" is called Z-evaluation. If A is not a member of only one point, the U is an uncertain variable.

In reality, Z-evaluation can be considered as a limitation on the U, which is defined - by the expression:

Prob (U is A) is B.

This means that we do not know the true probability density for U, but there is a limitation in the form of a fuzzy subset Р of the space P of all probability densities for U. This limitation is fuzzy probability of B. Let p be a density function on U. The probability density  (probability that U is A) is determined on the basis of determining the probability of a fuzzy subset of the proposed by Zadeh [6] as

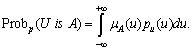
Then, the degree to which p satisfies Z-evaluation  is B is

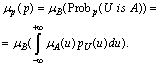
We take a following parametric distribution is taken in a form of р:

1.   Normal distribution, the density function of which is

In this situation, for any m,  we have

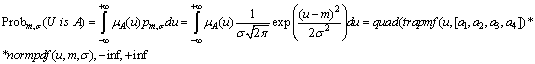
Then the space Р of probability distributions is the class of all normal distributions, each uniquely defined by its parameter m, .

2.   Uniform distribution, the density function of which is

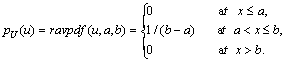
In this situation, for any m,  we have

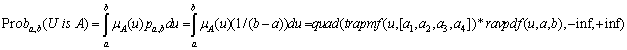
Then the space Р of probability distributions is the class of uniform distributions, each uniquely defined by its parameter a and b.

Consequently, operations on Z-number given in [15] will be sufficiently simplified.

5. Discussion of Experimental Results

Let us give a fuzzy sample of experimental data , ; here - n-dimensional input vector and  - output vector corresponding to it.

In general, it is required to build a model based on fuzzy inference rules using Z-estimation uncertainty:

.

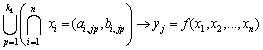This approach of using Z-numbers in the fuzzy output system gives the opportunity to take into account the uncertainty more effectively of when working with approximate, inaccurate information. We can confidently say that this algorithm can be developed with great success to find wide application in the solutions of both engineering and economic problems of various kinds.

Let us illustrate the work of the system in an example.

We consider three types of fuzzy models for assessing the status of poorly formalized process, the output of which is a linear and non-linear dependence.

1.   Fuzzy model, the output of which is a linear dependence:

If

...............................

,

then

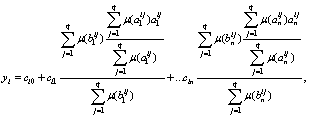
2.   Fuzzy model, the output of which is represented in the form of fuzzy terms:

If =(L, M) and =(L, M) and = (L, M)) or =(L, M) and =(L, M) and =(L, M) and =(L, M) and =(L, M) then =(H, M).

If =(L, M) and =(L, M) and =(L, M) and =(M, M) or =(L, M) and =(L, M) and =(L, M) and =(H, M) or =(L, M) and =(L, M) and =(M, M) and =(L, M) then =(HM, M).

If =(L, M) and =(L, M) and =(L, M) and =(HM, M) or =(L, M) and =(L, M) and =(HM, M) and =(M, HM) or =(L, M) and =(L, M) and =(M, HM) and =(H, HM) then =(M, HM).

If =(L, HM) and =(H, HM) and =(M, HM) and =(M, HM) or =(L, HM) and =(M, HM) and =(M, HM) and =(H, HM) then =(LM, M).

If =(M, HM) and =(H, HM) and =(M, HM) and =(H, HM) or =(H, HM) and =(H, HM) and =(M, HM) and =(H, HM) or =(H, HM) and =(H, HM) and =(H, HM) and =(H, HM) then =(L, M).

Here L-low, M-medium, LM- low medium, HM- higher medium, H-high.

3.   Fuzzy model, the output of which is represented as a non-linear dependence:

If

...............................

,

then

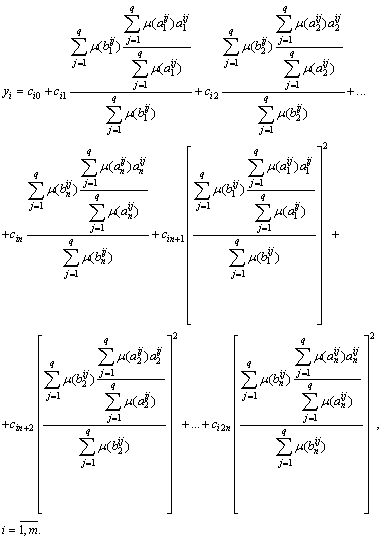
Software has been developed. In this embodiment, we used fuzzy inference algorithm, based on the conversion of Z-numbers in fuzzy numbers.

According to the results of the study, we have obtained a forecast of shortage in crop risk assessment, based on the construction of approximating models using training and testing of the risk of data (Figure 1). Charts of these relationships are shown in Figure 2.

In the proposed model, each input variable has its own membership functions of fuzzy terms (low, low medium, medium, higher medium, high), which are used in the equations.

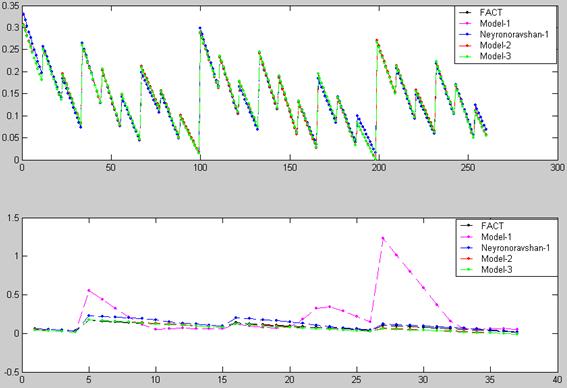
Fig. 1. Schedule risk assessment for training and testing data.

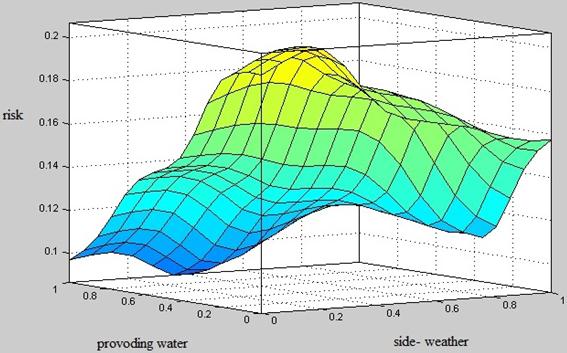
Fig. 2. The surface of the "input - output" for risk assessment.

As a direction for further work we can underline the development of the algorithm use of arithmetic discrete Z-numbers in systems of fuzzy output with a view to full implementation of Z-information display mechanisms that will bring the smallest loss of information contained in the Z-numbers.

6. Conclusion

The result of this work is the developed approach to the use of Z-numbers in the system of fuzzy output by converting Z-numbers in the classical fuzzy numbers and the development of an approach to decision-making, which summarizes the current expected utility approach in the case of Z-information. This approach, in contrast to other studies on decision-making within the Z-information based on a direct calculation of the Z numbers without converting them into fuzzy numbers. A direct calculation of the Z-numbers excludes loss of information related to the conversion. The approach used to solve poorly-formalized process state estimation problems. The results have showed the validity of the proposed approach.

References

1. Zadeh L. A. A note on a Z-number // Information Sciences USA, Vol 181, 2011, pp. 2923-2932 (in English).
2. Kang B., Wei D., Li Y., Deng Y. A Method of Converting Z-number to Classical Fuzzy Number //Journal of Information & Computational Science USA, 2012, Vol 9, Issue 3, pp. 703-709 (in English).
3. L. A. Zadeh, Fuzzy sets, Information and Control USA, 1965, Vol 8, pp. 338-353 (in English).
4. Kaufmann A., Gupta M. Introduction to fuzzy arithmetic: Theory and application // Van Nostrand Reinhold Co, New York, 1985, 359 p. (in English).
5. Klir G., Yuan B. Fuzzy Sets and Fuzzy Logic Theory and Applications //Prentice Hall, New Jersey, 1995, 592 p. (in English).
6. Kang B., Wei D., Li Y., Deng Y. Decision Making Using Z-numbers under Uncertain Environment // Journal of Information & Computational Science. USA, 2012, Vol. 8, Issue 7, pp. 2807-2814 (in English).
7. Yager R. R. On a View of Zadeh's Z-Numbers //Advances in Computational Intelligence, Communications in Computer and Information Science, USA, 2012, Vol 299, pp. 90-101 (in English).
8. Yager R. R. On Z-valuations using Zadeh`s Z-numbers // International Journal of Intelligent Systems 2012, Vol 27, pp. 259-278 (in English).
9. Sevastianov P. Numerical methods for interval and fuzzy number comparison based on the probabilistic approach and Dempster–Shafer theory // Information Sciences 2007, Vol. 177, pp. 4645-4661 (in English).
10. Zhai D., Mendel J. Uncertainty measures for general type-2 fuzzy sets// Information Sciences USA, 2011 Vol. 181 (3), pp. 503-518 (in English).
11. Zadeh L. A. Methods and systems for applications with Z-numbers// United States Patent, Patent No.: 2012, US 8,311,973 B1, Date of Patent: Nov. 13, (in English).
12. Aliev R. A., Zeinalova L. M. Decision making under Z-information // In: P. Guo, W. Pedrycz (Eds.), Human Centric Decision-Making Models for Social Sciences (Studies in Computational Intelligence), Springer, Berlin Heidelberg, 2013 (in English).
13. Aliev R. A., Pedrycz W., Fazlollahi B., Huseynov O. H., Alizadeh A. V., Guirimov B. G. Fuzzy logic-based generalized decision theory with imperfect information // Information Sciences 2011, Vol. 189, pp. 18-42 (in English).
14. Farina M., Amato P. A fuzzy definition of "optimality" for many-criteria optimization problems // IEEE Transactions on Systems, Man and Cybernetics, Part A: Systems and Humans 2004, Vol. 34 (3) pp. 315-326 (in English).
15. Aliev R. A. Fundamentals of the Fuzzy Logic-Based Generalized Theory of Decisions //Studies in Fuzziness and Soft Computing Springer, Berlin Heidelberg, 2013, 293, (in English).