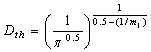Calculations for Damage Strengh to Linear Elastic Materials-The Genetic Elements and Clone Technology in Mechanics and Engineering Fields
Yangui Yu
Zhejiang Guangxin New Technology Application Academy of Electromechanical and Chemical Engineering, Hangzhou, China
Email address
Citation
Yangui Yu. Calculations for Damage Strengh to Linear Elastic Materials-The Genetic Elements and Clone Technology in Mechanics and Engineering Fields. Journal of Materials Sciences and Applications. Vol. 2, No. 6, 2016, pp. 39-50.
Abstract
The author bases on the principles of similar to the genetic genes in the life sciences, discovers some new constants shown material properties from micro to macro damage, and proposes some new computing models which are the threshold values and the critical ones on damage to some metallic materials; That is to use the theoretical approach, to adopt the conventional material constants, to derive the new mathematical models and the stress factor of called damage strength, to provide simple assessment criterions on the damage strength and the calculating methods in each stage. In addition, it supplements again the comprehensive figure of the material behaviours; gives yet a detailed calculating example for a safety assessment. This works may be there are practical significances for make linking and communication between the modern fracture mechanics and the damage mechanics, for the decreasing experiments.
Keywords
Principles of Genes, Conventional Constants, Threshold Value of Damage, Critical Value of Damade, Damage Factor, Assessment Method
1. Introduction
As is well-known, in the traditional materials mechanics, in describing materials behaviours and their strength problems, its main calculating parameters are the stress 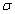 , the strain
, the strain 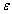 and relevant material constants, e.g. yield stress
and relevant material constants, e.g. yield stress 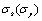 , elasticity modulus
, elasticity modulus 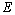 and reduction of area
and reduction of area 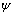 , etc. And in the fatigue discipline, it also adopts the stress
, etc. And in the fatigue discipline, it also adopts the stress 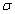 and the strain
and the strain 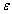 as calculating parameters to use the fatigue strength coefficient
as calculating parameters to use the fatigue strength coefficient 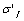 and the fatigue ductility coefficient
and the fatigue ductility coefficient 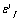 , etc., as its material constants. In the damage mechanics, it is based on the damage parameter
, etc., as its material constants. In the damage mechanics, it is based on the damage parameter 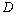 as its variable to calculate life prediction problems. In the fracture mechanics, it describes the materials behaviours at the crack tip on the strength problems, which is based on the crack size
as its variable to calculate life prediction problems. In the fracture mechanics, it describes the materials behaviours at the crack tip on the strength problems, which is based on the crack size 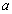 as its variable, to use the fracture toughness
as its variable, to use the fracture toughness 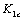 and the critical crack tip open displacement
and the critical crack tip open displacement 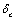 as its material constants.
as its material constants.
To refer to the genes and clone technologies in the life science in [1-10], which traits consist in: they had both self-genetic properties, and had the transferable and the recombination properties. In fact, in the model 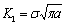 [11-13] of the stress intensity factor in fracture mechanics, in the crack tip open displacement
[11-13] of the stress intensity factor in fracture mechanics, in the crack tip open displacement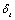 , in their critical values
, in their critical values 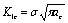 and the
and the 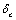 , all include the parameters
, all include the parameters 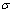 ,
,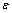 ,
,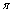 and their material constants
and their material constants 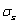 ,
,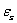 and fracture stress
and fracture stress 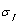 etc. Here for the stress
etc. Here for the stress 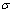 , the strain
, the strain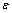 and its relevant material constants
and its relevant material constants 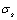 and
and 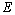 , etc, in the materials mechanics can be considered as the genetic elements; the parameters
, etc, in the materials mechanics can be considered as the genetic elements; the parameters 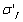 ,
, 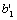 ,
, 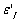 ,
, 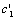 ,
, 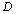 , etc, in the fatigue discipline and the damage mechanics can also be considered as the genetic elements; and the crack size
, etc, in the fatigue discipline and the damage mechanics can also be considered as the genetic elements; and the crack size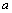 in the fracture mechanics can also be considered as the genetic elements. If can make a link among the materials mechanics, the fatigue subject, the damage mechanics and the fracture mechanics, and if we can provide some conversion methods to make them also convert each other for their relations between the variables, between the material constants and between the dimensional units in the equations, then it would realize this goal. For example, here can consider them as genes for the stress
in the fracture mechanics can also be considered as the genetic elements. If can make a link among the materials mechanics, the fatigue subject, the damage mechanics and the fracture mechanics, and if we can provide some conversion methods to make them also convert each other for their relations between the variables, between the material constants and between the dimensional units in the equations, then it would realize this goal. For example, here can consider them as genes for the stress 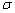 and their material constants
and their material constants 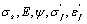 , to make them combine with the variable
, to make them combine with the variable 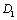 of micro-damage, which are together transferred into micro-damage-mechanics, and in combination with the variable
of micro-damage, which are together transferred into micro-damage-mechanics, and in combination with the variable 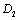 of macro-damage, which are transferred into macro-damage-mechanics. In the same way, here can also consider them as genes for the stress
of macro-damage, which are transferred into macro-damage-mechanics. In the same way, here can also consider them as genes for the stress 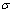 and
and 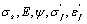 , to make them combine with the variable
, to make them combine with the variable 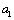 of short crack, which are together transferred into micro-fracture-mechanics, and combine with the variable
of short crack, which are together transferred into micro-fracture-mechanics, and combine with the variable  of long crack, which are transferred into macro-fracture-mechanics. Then it is able by these parameters
of long crack, which are transferred into macro-fracture-mechanics. Then it is able by these parameters 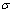 ,
, 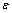 ,
, 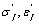 , etc, to establish their renewing models for the driving forces, for the crack propagating rates and the life equations, or for the damage growth rates and the life equations. Even can also adopt the variable
, etc, to establish their renewing models for the driving forces, for the crack propagating rates and the life equations, or for the damage growth rates and the life equations. Even can also adopt the variable 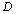 or
or 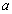 to describe materials behaviours in the whole process.
to describe materials behaviours in the whole process.
Above the peculiarities of those parameters and material constants which they are as compared to those ones in the life sciences, they are in different disciplines, but for both all have own inheritable properties (similar to genetic elements), and for both all have the traits of the transferable and the recombination on the epistemology and on the methodology, which, in practice, are all very similar.
Based on the cognitions and the concepts mentioned above, the author draws a link among the engineering materials, the materials mechanics, the fatigue, the damage mechanics and the fracture mechanics, for relationships among their parameters are analysed, for their equations are derived, for their dimensional units convert each other; then to derive a lot of the new mathematical model, and for these newly made computing models are calculated, checked again and again; finally, to provide the calculable equations and expressions (1-17). This is to try to set up communications among many disciplines mentioned above and thereby solve those problems in crack (damage) growth process about which are the driving forces, the strength criteria, the rates of crack propagation and the life calculation, for which become the calculable ones, so that they would be applied in practical engineering. If can realize the goals, it will have practical significances for the design of machineries and structures and for the computational analysis of safe operations and assessments where they are widely distributed in communications and transportation, the aerospace industry, mechanical engineering and other fields.
2. A New Comprehensive Figure on Materials Behaviours
About problems among branch disciplines on fatigue-damage-fracture; about problems among the traditional material mechanics and the modern mechanics for communications and connecting their relations with each other, we must study and find out their correlations between the equations, even the relations between variables, between the material constants, and between the curves. This is because all the significant factors are to be researched and described for materials behaviours at each stage even in the whole process and are also all to have a lot of significations for the engineering calculations and designs. Therefore, we should research and find an effective tool used for analyzing the problems above mentioned. Here, the author provides the "Comprehensive figure of materials behaviors" as Figure 1 (or the bidirectional combined coordinate system and simplified schematic curves in the whole process, or combined cross figure) that both is a principle figure of materials behaviors under monotonous loading, and is one under fatigue loading. It is also a comprehensive figure of multidisciplinary. Here in two problems to present as below:
2.1. Explanations on Their Geometrical and Physical Meanings for the Compositions of Coordinate System
In figure 1, it was being provided by the present author; at this time it has been corrected and complemented, that is, diagrammatically shown for the damage growth process or crack propagation process of materials behavior at each stage and in the whole course.
For the coordinate system, it is to consist of six abscissa axes 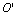 I",
I", 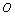 I’,
I’, 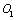 I,
I, 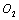 II,
II, 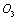 III,
III, 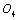 IV and a bidirectional ordinate axis
IV and a bidirectional ordinate axis 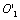
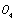 . For the area between the axes
. For the area between the axes 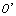 I" and
I" and 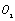 I, it was an area applied as by the traditional material mechanics. Currently, it can also be applied for the micro-damage area by the very high cycle fatigue. Between the axes
I, it was an area applied as by the traditional material mechanics. Currently, it can also be applied for the micro-damage area by the very high cycle fatigue. Between the axes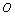 I’ and
I’ and 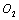 II, it is calculating area applied for the micro-damage mechanics and the micro-fracture mechanics. For the areas among the
II, it is calculating area applied for the micro-damage mechanics and the micro-fracture mechanics. For the areas among the 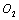 II, the
II, the 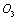 III and
III and 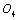 IV where they are calculatied and applied by the macro-damage mechanics and the macro-fracture mechanic. But for between the axes
IV where they are calculatied and applied by the macro-damage mechanics and the macro-fracture mechanic. But for between the axes  I and
I and  II, it is calculated and applied in areas both for the micro-damage mechanics and for the macro-damage mechanics, or both for the micro-fracture mechanics and for the macro-fracture mechanics.
II, it is calculated and applied in areas both for the micro-damage mechanics and for the macro-damage mechanics, or both for the micro-fracture mechanics and for the macro-fracture mechanics.
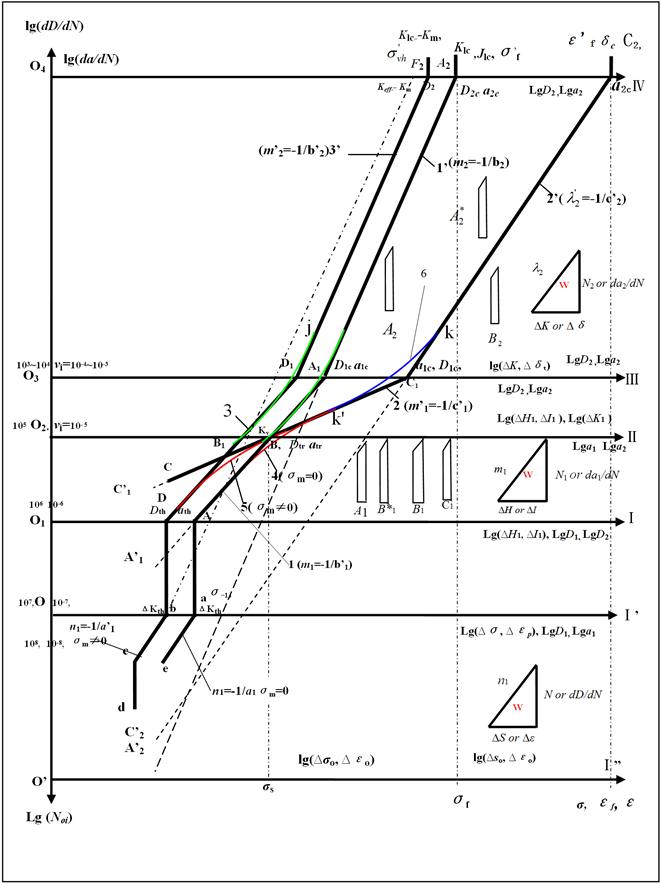
Figure 1. Comprehensive figure of material behaviors 1 (Or called calculating figure of material behaviors or bidirectional combined coordinate system and simplified schematic curves in the whole process).
On the abscissa axes  I" and
I" and 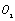 I, they are represented with parameters the stress
I, they are represented with parameters the stress 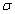 and the strain
and the strain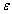 as variables. On the abscissa axes
as variables. On the abscissa axes 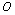 I’ there are the fatigue limit
I’ there are the fatigue limit 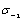 at point "a"
at point "a" 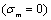 and "b"
and "b" 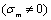 that they just are the locations placed at threshold values for crack (damage) growth to some materials; on the abscissa axes
that they just are the locations placed at threshold values for crack (damage) growth to some materials; on the abscissa axes 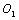 I there are points "A" and "D" that just are the locations placed at threshold values to another materials. On the abscissa axes
I there are points "A" and "D" that just are the locations placed at threshold values to another materials. On the abscissa axes 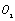 I and
I and 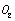 Ⅱ that they could all represented as variables with the stress intensity factor range
Ⅱ that they could all represented as variables with the stress intensity factor range 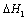 of short crack, and the strain intensity factor
of short crack, and the strain intensity factor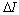 , and the stress intensity factor range
, and the stress intensity factor range 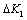 of long crack. On the other hand, they both are yet represented as variables with the short crack
of long crack. On the other hand, they both are yet represented as variables with the short crack 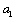 and the long crack (or damage and
and the long crack (or damage and 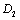 ). And here there are materal constants of two that they are defined as the critical factor
). And here there are materal constants of two that they are defined as the critical factor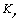 of crack-stress-intensity and the critical factor
of crack-stress-intensity and the critical factor 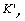 of the damage-stress-intensity at the first stage, where that are just the transition parameters corresponded to the critical crack size
of the damage-stress-intensity at the first stage, where that are just the transition parameters corresponded to the critical crack size 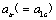 or the critical value of damage
or the critical value of damage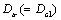 , they are just placed at point at the point B
, they are just placed at point at the point B 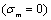 and at point
and at point 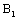
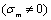 corresponded to yield stress, that are also the boundary between short crack and long crack growth behaviors; but for some brittle materials would be happened to fracture to this point when their stresses are loaded to this level. On the abscissa axes O3 III, it is represented as variable with the stress intensity factor
corresponded to yield stress, that are also the boundary between short crack and long crack growth behaviors; but for some brittle materials would be happened to fracture to this point when their stresses are loaded to this level. On the abscissa axes O3 III, it is represented as variable with the stress intensity factor 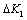 (or
(or 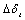 ) of long crack; it is a boundary between the first stage and the second stage for some elastic-plastic materials. On this axes O3 III there are the critical points at D1, A1, and C1 (D1c, A1c). On abscissa
) of long crack; it is a boundary between the first stage and the second stage for some elastic-plastic materials. On this axes O3 III there are the critical points at D1, A1, and C1 (D1c, A1c). On abscissa 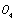 IV, the point
IV, the point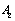 is corresponding to the fatigue strength coefficient
is corresponding to the fatigue strength coefficient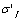 , the critical stress intensity factor values
, the critical stress intensity factor values 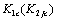 and the critical values
and the critical values 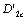 and
and 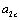 for the mean stress
for the mean stress 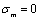 ; the point
; the point 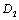 is corresponding to the
is corresponding to the 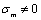 ; the point
; the point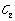 corresponding to the fatigue ductility coefficient
corresponding to the fatigue ductility coefficient 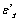 and critical crack tip open displacement value
and critical crack tip open displacement value 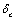 ; the point
; the point 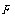 corresponding to a very high cycle fatigue strength coefficient
corresponding to a very high cycle fatigue strength coefficient 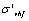 . In addition on the same
. In addition on the same 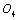 IV, there are yet another critical values
IV, there are yet another critical values 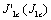 , etc. in the long crack propagation process.
, etc. in the long crack propagation process.
For an ordinate axis, an upward direction along the ordinate axis is represented as crack growth rate 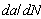 or damage growth rate
or damage growth rate 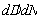 in each stage and the whole process. But a downward direction is represented as life
in each stage and the whole process. But a downward direction is represented as life 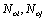 in each stage and the whole lifetime
in each stage and the whole lifetime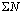 .
.
In the area between axes 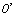 I" and
I" and 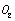 II, it is the fatigue history from un-crack to micro-crack initiation. In the area between axes
II, it is the fatigue history from un-crack to micro-crack initiation. In the area between axes 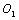 I’ and
I’ and 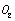 II, it is the fatigue history relative to life
II, it is the fatigue history relative to life 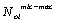 from micro-crack growth to macro-crack forming. Consequently, the distance
from micro-crack growth to macro-crack forming. Consequently, the distance 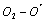 on ordinate axis is as the history relating to life
on ordinate axis is as the history relating to life  from grains size to micro-crack initiation until macro-crack forming; the distance
from grains size to micro-crack initiation until macro-crack forming; the distance 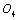 -
- is as the history relating to the lifetime life
is as the history relating to the lifetime life  from micro-crack initiation until fracture.
from micro-crack initiation until fracture.
In the crack forming stage, the partial coordinate system made up of the upward and the ordinate axes 
 and the abscissa axes
and the abscissa axes 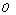 I’,
I’,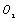 I and
I and 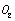 Ⅱ is represented as the relationship between the crack growth rate
Ⅱ is represented as the relationship between the crack growth rate 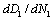 (or the short crack growth rate
(or the short crack growth rate 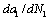 ) and the crack-stressfactor range
) and the crack-stressfactor range 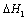 (or the damage strain factor range
(or the damage strain factor range 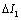 ). In the macro-crack growth stage, the partial coordinate system made up with the ordinate axis
). In the macro-crack growth stage, the partial coordinate system made up with the ordinate axis 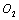
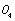 and abscissa
and abscissa 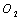 II,
II, 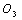 III and
III and 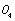 IV at the same direction is represented to be the relationship between the macro-crack growth rate and the stress intensity factor range
IV at the same direction is represented to be the relationship between the macro-crack growth rate and the stress intensity factor range 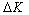 ,
, 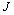 -integral range
-integral range 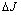 and crack tip displacement range
and crack tip displacement range 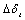 (
(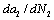 -
-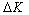 ,
,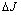 and
and 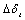 ). Inversely, the coordinate systems made up of the downward ordinate axis
). Inversely, the coordinate systems made up of the downward ordinate axis 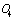
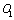 and the abscissa axes
and the abscissa axes 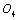 IV,
IV, 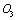 III,
III, 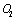 II,,
II,, 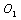 I, and
I, and 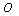 I’ are represented respectively as the relationship between the
I’ are represented respectively as the relationship between the 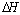 -,
-, 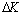 - range and each stage life
- range and each stage life 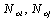 and the lifetime
and the lifetime 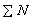 (or between the
(or between the 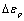 -,
-, 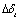 - range and the life
- range and the life 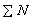 ).
).
2.2. Explanations on the Physical and Geometrical Meanings of Relevant Curves
The curve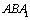 is represented as the varying laws as the behaviours of the elastic materials or some elastic-plastic ones under high cycle loading in the macro-crack-forming stage (the first stage): positive direction
is represented as the varying laws as the behaviours of the elastic materials or some elastic-plastic ones under high cycle loading in the macro-crack-forming stage (the first stage): positive direction 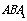 represented as the relations between
represented as the relations between 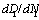 (or
(or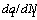 )-
)-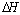 ; inverted
; inverted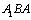 , between the
, between the 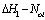 . The curve
. The curve 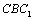 is represented as the varying laws of the behaviours of the elastic-plastic materials or some plastic ones under low-cycle loading at the macro-crack forming stage: positive direction
is represented as the varying laws of the behaviours of the elastic-plastic materials or some plastic ones under low-cycle loading at the macro-crack forming stage: positive direction 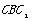 is represented as the relations between
is represented as the relations between 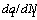 -
-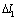 ; inverted
; inverted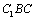 , the relations between the
, the relations between the 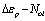 .
.
The curve 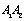 in the crack growth stage (the second stage) is showed as under high cycle loading: positive direction
in the crack growth stage (the second stage) is showed as under high cycle loading: positive direction 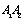 showed as
showed as 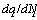 -
-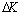 (
(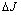 ); inverted
); inverted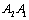 , between the
, between the 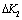 ,
,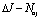 . The
. The 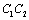 is showed as: the positive, relation between the
is showed as: the positive, relation between the 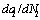 -
-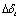 under low-cycle loading, inverted
under low-cycle loading, inverted 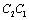 , between
, between 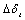 (
(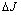 )-
)-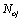 . By the way, the curves
. By the way, the curves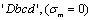 and the
and the 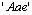 (
(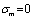 ) are represented as the laws under the very high cycle fatigue.
) are represented as the laws under the very high cycle fatigue.
It should yet point that the curve 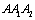 (1-1’) is depicted as the rate curve of damage (crack) growth in whole process under symmetrical and high cycle loading (i.e. zero mean stress,
(1-1’) is depicted as the rate curve of damage (crack) growth in whole process under symmetrical and high cycle loading (i.e. zero mean stress, 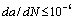 ); the curve
); the curve 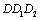 (3-3’), as the rate curve under unsymmetrical cycle loading (i.e. non-zero mean stress, ). The curve
(3-3’), as the rate curve under unsymmetrical cycle loading (i.e. non-zero mean stress, ). The curve 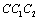 (2-2’) is depicted as the rate curve under low cycle loading. The curve
(2-2’) is depicted as the rate curve under low cycle loading. The curve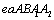 is depicted as the damage (crack) growth rate curve in whole process under very high cycle loading (
is depicted as the damage (crack) growth rate curve in whole process under very high cycle loading (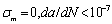 ), the curves
), the curves 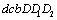 and
and 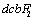 are depicted as ones of the damage (crack) growth rates in whole process under very high cycle loading (
are depicted as ones of the damage (crack) growth rates in whole process under very high cycle loading (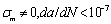 ). Inversely, the curve
). Inversely, the curve 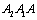 is depicted as the lifetime curve under symmetrical cycle loading (i.e. zero mean stress,
is depicted as the lifetime curve under symmetrical cycle loading (i.e. zero mean stress,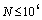 ), the curve
), the curve 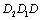 , as the lifetime curve under unsymmetrical cycle loading
, as the lifetime curve under unsymmetrical cycle loading 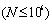 . The curve
. The curve 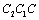 is depicted as the lifetime curve under low cycle loading. On the other hand, the curve
is depicted as the lifetime curve under low cycle loading. On the other hand, the curve 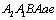 is as the lifetime one in whole process included very high cycle fatigue (), the curves
is as the lifetime one in whole process included very high cycle fatigue (), the curves 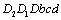 and
and 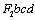 are all depicted as the lifetime ones in whole process
are all depicted as the lifetime ones in whole process 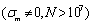 .
.
It should also be explained that the comprehensive figure 1 of the materials behaviours may be a complement as a
fundamental research; that is a tool to design and calculate for different structures and materials under different loading conditions, and it is also a bridge to communicate and link the traditional material mechanics and the modern mechanics.
3. Strengh Calculations on Damage Under Monotonic Loading
Here the damage variables D for describing the damage growth process that are defined as follows:
1). From micro-crack initiation to macro-crack forming process, it is defined in the crack forming stage or defined in the first stage. If applying the concept of the damage mechanics, it is defined in the micro-damage stage where it adopts variable D1 called the micro-damage variable, which is corresponded to the variable a1 of a short crack that it is corresponding curve AA1 in figure 2;
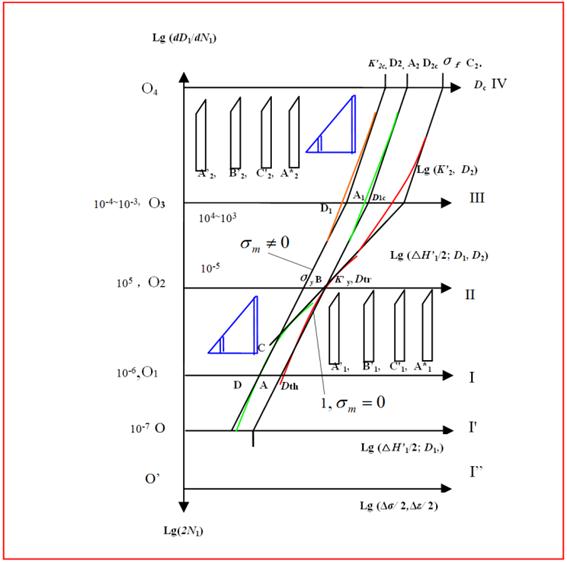
Figure 2. Figure of material damage behaviors in whole process.
2). From the macro-crack propagation to the fracture process is defined in the crack growth stage, or defined in the second stage, here is also applying the concept of the damage mechanics, it is defined in the macro-damage stage. The damage variable D2 of this stage is called in the macro damage variable, it corresponds to the variable a2 of the long crack that it is corresponding curve A1A2 in figure 2;
3). From micro-damages to full failure of a material, to adopt the parameter D as the variable in the whole process, it corresponds to the crack variable a in the whole process from short crack to long crack growth until full fracture that it is corresponding curve AA1 A2 in figure 2.
3.1. About the Driving Force and theThreshold Value on Damage
In the figure 2, it can be seen that differences with the loading ways and the stress levels, for the general steels, their behaviours were always shown defferences in the each stages, but they are all to exist the threshold values 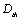 of the damage, only depended on the exponents
of the damage, only depended on the exponents 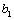 related to the material character in table 1.
related to the material character in table 1.
Table 1. Data of threshold values of damage.
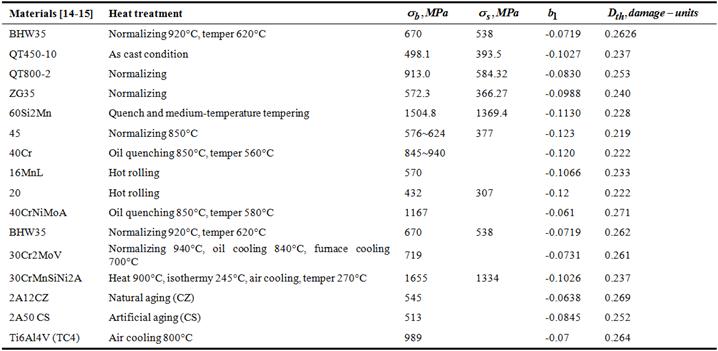
It should point the location of the threshold value 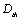 of damage is at the point A where it is at the intersection one between the straight line AA1 and the abscissa axis
of damage is at the point A where it is at the intersection one between the straight line AA1 and the abscissa axis 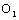 I in figure 2. And the threshld
I in figure 2. And the threshld 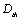 can be calculable one with as following formula under the monotonous loading, it should be [16]
can be calculable one with as following formula under the monotonous loading, it should be [16]
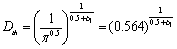
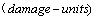 (1)
(1)
Or
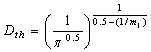
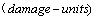 (2)
(2)
The range of the 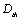 is in 0.21~0.275 (damage-units), it is equivalent to the lengths 0.21~0.275 (mm) of short crack. For linear elastic materials, to make the
is in 0.21~0.275 (damage-units), it is equivalent to the lengths 0.21~0.275 (mm) of short crack. For linear elastic materials, to make the 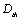 is combined with the stress
is combined with the stress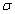 , so that it can form a model of the driving force that is as below,
, so that it can form a model of the driving force that is as below,
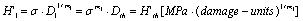 (3)
(3)
In the formula (3), 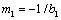 ; The
; The 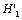 is defined as the stress intensity factor of micro damage. Because the variable
is defined as the stress intensity factor of micro damage. Because the variable 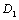 is a dimensionless value, it is equivalent to the short crack size
is a dimensionless value, it is equivalent to the short crack size 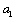 . Here it must be defined in "1mm length of crack " equivalent to "1-unit damage value", in "1m length of crack" equivalent to "1000 damage units" [17-19]. In an ordinary way, the
. Here it must be defined in "1mm length of crack " equivalent to "1-unit damage value", in "1m length of crack" equivalent to "1000 damage units" [17-19]. In an ordinary way, the 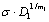 may be: the
may be: the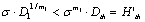 or
or 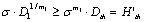 , the strength criterions for them is as below,
, the strength criterions for them is as below,
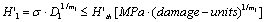 (4)
(4)
Or
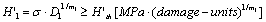 (5)
(5)
Where the 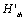 is defined as the threshold factor of damage. If to take the yield stress to replace the in the equaton , it is come as following form(4)
is defined as the threshold factor of damage. If to take the yield stress to replace the in the equaton , it is come as following form(4)
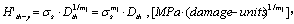 (6)
(6)
Then the 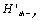 is defined as the threshold factor of the yield stress, so that the
is defined as the threshold factor of the yield stress, so that the 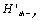 must be the only the constant showing a material property; And the damage of a material is sure to grow if a
must be the only the constant showing a material property; And the damage of a material is sure to grow if a 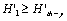 .
.
3.2. Strength Calculation on Damage at the First Stage
When the damage growth gets to the micro damage stage where it is corresponding to the curve 1 (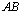 ) between abscissa axis O1 I and the O2 II in figure 2. If the stress inside a structure component is loaded to the yield stress (at point B on abscissa axis O2 II) or over this level to the A1 (at point A1 on abscissa axis O3 III), then it can set up a criterion of the damage strength for it in the first stage, that is as below form [6]
) between abscissa axis O1 I and the O2 II in figure 2. If the stress inside a structure component is loaded to the yield stress (at point B on abscissa axis O2 II) or over this level to the A1 (at point A1 on abscissa axis O3 III), then it can set up a criterion of the damage strength for it in the first stage, that is as below form [6]
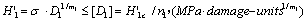 (7)
(7)
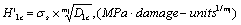 (8)
(8)
Where the damage value 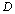 may be to take the size of preexisting flaw in a component, it can also be calculated by a designer in designing. Then when the design stress is less than the yield stress (
may be to take the size of preexisting flaw in a component, it can also be calculated by a designer in designing. Then when the design stress is less than the yield stress (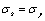 ), the damage value can be adopted with following formula,
), the damage value can be adopted with following formula,
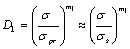 , (9)
, (9)
Where the 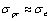 is a stress value of proportional limit (approximating to the elastic limit, it can also approximatively be took for the yield stress as the data is to lack. The
is a stress value of proportional limit (approximating to the elastic limit, it can also approximatively be took for the yield stress as the data is to lack. The 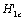 in (7) is defined as a critical value of the stress intensity factor on damage, the
in (7) is defined as a critical value of the stress intensity factor on damage, the 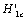 is a value corresponded to the critical value
is a value corresponded to the critical value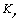 and the transition value Dtr of damage, also is the boundary between the short crack and the long crack. Their locations are respectively at points B on abscissa axis O2-II (in Fig. 2). For some cast iron, brittle materials and low toughness steels, which could be happened to fracture when their stresses are loaded to this level.
and the transition value Dtr of damage, also is the boundary between the short crack and the long crack. Their locations are respectively at points B on abscissa axis O2-II (in Fig. 2). For some cast iron, brittle materials and low toughness steels, which could be happened to fracture when their stresses are loaded to this level.
As is well know the mathematic model to describe a long crack in fracture mechanics that it is to adopt these "genes" 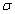 and
and 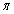 and crack variable
and crack variable 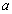 , thereby to make the stress intensity factor
, thereby to make the stress intensity factor 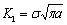 ; Here to take the macro damage variable
; Here to take the macro damage variable 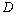 in the name of macro damage mechanics to displace the crack size
in the name of macro damage mechanics to displace the crack size 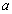 inside the
inside the 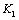 , then it can still derive the equation of driving force for the describing behavior of it, that is as following form [10].
, then it can still derive the equation of driving force for the describing behavior of it, that is as following form [10].
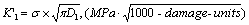 (10)
(10)
Here is sure to explain, the area between the abscissa axis O1-I and the O2-II in fig. 2, the 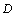 -value from the threshold
-value from the threshold 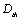 to
to 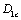
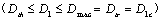 , there are the mathematic models of the stress factors of two kinds, which are all suited in the section. In addition to above equations (6-8) can be applied, in theory another mathematic models (9-13) are still suitable in the first stage.
, there are the mathematic models of the stress factors of two kinds, which are all suited in the section. In addition to above equations (6-8) can be applied, in theory another mathematic models (9-13) are still suitable in the first stage.
Where the 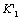 is a stress intensity factor of the macro damage that it is equivalent to
is a stress intensity factor of the macro damage that it is equivalent to 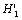 , but their dimensions and units are differences at this same point. For that corresponding to size
, but their dimensions and units are differences at this same point. For that corresponding to size 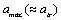 of forming macro crack, that is the very that damage factor
of forming macro crack, that is the very that damage factor 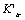 of corresponded to the damage-value
of corresponded to the damage-value 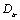 at transition point, also a the critical value
at transition point, also a the critical value 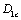 in the first stage, where is just at point B corresponding yield stress
in the first stage, where is just at point B corresponding yield stress 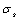 on abscissa axis O2-II, and is on that boundary between the first stage and the second stage in fig. 2. Then the model of driving force at this point should be as follow
on abscissa axis O2-II, and is on that boundary between the first stage and the second stage in fig. 2. Then the model of driving force at this point should be as follow
 (11)
(11)
Here it need yet explain, this factor 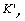 should theoretically be equivalent to above mentioned the
should theoretically be equivalent to above mentioned the 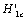 in first stage, although the dimensions and units between them are differences. Therefore the strength criterion of its damage should be calculated as following form,
in first stage, although the dimensions and units between them are differences. Therefore the strength criterion of its damage should be calculated as following form,
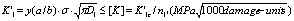 (12)
(12)
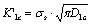
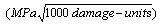 (13)
(13)
Where the 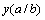 [20-21] is a correcting factor related with the shape and the size of a crack.
[20-21] is a correcting factor related with the shape and the size of a crack. 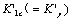 is a the critical value of damage, they are all corresponding to the yield stress
is a the critical value of damage, they are all corresponding to the yield stress 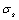 and the critical value
and the critical value 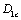 of damage. It shoud point, because the yield stresses
of damage. It shoud point, because the yield stresses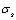 is the constant of uniquenesses for a material, the critical values of the damage
is the constant of uniquenesses for a material, the critical values of the damage 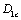 and the factor
and the factor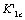 related the
related the 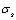 should also be considered as the only ones, and can also be applied as an important parameters showed its property. In practice, the critical value
should also be considered as the only ones, and can also be applied as an important parameters showed its property. In practice, the critical value 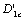 could be calculated by means of below formula:
could be calculated by means of below formula:
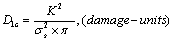 (14)
(14)
Where 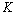 is a strength coefficient under monotonic loading. It has to point the calculating equations merntioned above are only suitable for some brittle materials and strain hardening ones, it does not suit the materials of strain softening.
is a strength coefficient under monotonic loading. It has to point the calculating equations merntioned above are only suitable for some brittle materials and strain hardening ones, it does not suit the materials of strain softening.
In the table 2, here are listed to the critical values 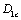 of damage for 13 kinds of materials.
of damage for 13 kinds of materials.
Table 2. The critical values 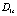 of damage.
of damage.
| Materials [14-15] | σb, MPa | σs, MPa | K, MPa | D1c |
| Hot rolled sheet 1005-1009 | 345 | 262 | 531 | 1.31 |
| Steel: 1005-1009 Cold-draw sheet | 414 | 400 | 524 | 0.546 |
| RQC-100, Hot rolled sheet | 931 | 883 | 1172 | 0.561 |
| 4340, quench and tempering | 1241 | 1172 | 1579 | 0.578 |
| Aluminum 2024-T3 | 469 | 379 | 455 | 0.46 |
| 30CrMnSiA, ① Hardening and tempering | 1177 | 1104.5 | 1475.76 | 0.568 |
| LC4CS, ① Heat treatment-CS | 613.9 | 570.8 | 775.05 | 0.587 |
| 40Cr ③ | 940 | 805 | 1592 | 1.25 |
| 60Si2Mn, quench, medium-temperature tempering ③ | 1504.8 | 1369 | 1721 | 0.503 |
| QT800-2, ② normalizing | 913 | 584.3 | 1777 | 2.94 |
| QT600-2, (B), ② normalizing | 748.4 | 456.5 | 1440 | 3.167 |
| QT600-2, (A) ② normalizing | 677 | 521.3 | 1622 | 3.08 |
| ZG35 ② normalizing | 572.3 | 366.3 | 1218 | 3.51 |
Note: 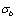 is a strength limit;
is a strength limit;  is an yield limit;
is an yield limit;
(A)-Bar  ; (B)-Y-type test specimen;
; (B)-Y-type test specimen;
①---The Masing’s materials; ②---The cycle-harden material ③-Cyclic softening.
It could see from table 2 where the materials from number 1 to 9 are the steels, their critical values of damage are 0.43~1.42 damage-units in first stage (equivalent to 0.43~1.42mm of the crack sizes); The materials from number 10 to 13 are the nodular cast irons and a cast iron respectively, their critical values of damage are 2.94~3.51 damage-units. In practice, because they get already the critical values of the fracture at the first stage under yield stress, then those materials will occur the failures.
3.3. Strength Calculation on Damage at the Second Stage
When the damage growth gets to the macro damage stage, where it is corresponding to the curve 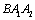 in figure 2. In this stage, for the behaviour of some materials corresponding curve
in figure 2. In this stage, for the behaviour of some materials corresponding curve 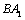 between the abscissa axis OII and the O3III, they form the critical values
between the abscissa axis OII and the O3III, they form the critical values 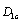 of macro damage are usually later than those brittle materials, their life are also longer, so the transition points between two stages in damage process are on the abscissa axis O3III that just is as the boundary of them. In this case that strength criterion (11-12) on damage in first stage can still be sutied for calculations in the second stage.
of macro damage are usually later than those brittle materials, their life are also longer, so the transition points between two stages in damage process are on the abscissa axis O3III that just is as the boundary of them. In this case that strength criterion (11-12) on damage in first stage can still be sutied for calculations in the second stage.
By the way, when a structure is calculating in design, if the work sress greater than the yield stress, then the damage value 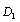 in the equation (11) can also be calculated by following formula
in the equation (11) can also be calculated by following formula
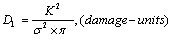 (15)
(15)
When the damage growth over the abscissa axis O3III in figure 2, the strength criterion of damage at later time in the second staege should be as following form
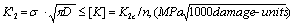 (16)
(16)
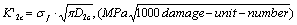 (17)
(17)
Where the 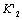 is defined as the stress factor of damage in the second, the
is defined as the stress factor of damage in the second, the 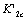 is a critical factor of damage that it is equivalent to the critical stress intensity factor
is a critical factor of damage that it is equivalent to the critical stress intensity factor 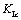 in fracture mechanics. The
in fracture mechanics. The 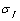 is a fracture stress, the
is a fracture stress, the 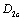 is a critical value of momentary fracture where it is at the crossing point A2 on the abscissa axis O4-Ⅳ and the straight line 1
is a critical value of momentary fracture where it is at the crossing point A2 on the abscissa axis O4-Ⅳ and the straight line 1 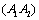 in fig. 2.
in fig. 2.
It should yet explain because the 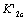 is also a material constant, it must be the data of uniqueness to show a material performance, and it could be calculated out by mens of the fracture stress
is also a material constant, it must be the data of uniqueness to show a material performance, and it could be calculated out by mens of the fracture stress 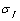 (table 2). So that the critical value of damage
(table 2). So that the critical value of damage 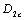 under corresponding to the true stress
under corresponding to the true stress 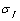 should also be the only data. In theory, it must be there is as following functional relationship,
should also be the only data. In theory, it must be there is as following functional relationship,
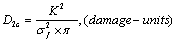 (18)
(18)
In the table 3 to include the critical values 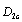 of some materials.
of some materials.
Table 3. The critical values 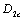 of momentary fracture.
of momentary fracture.
| Materials [14-15] | σb, MPa | σs, MPa | K, MPa | σf, MPa | D2c damage-units |
| Hot rolled sheet 1005-1009 | 345 | 262 | 531 | 848 | 0.125 |
| Steel: 1005-1009 Cold-draw sheet | 414 | 400 | 524 | 841 | 0.124 |
| RQC-100, Hot rolled sheet | 931 | 883 | 1172 | 1330 | 0.247 |
| 4340, quench and tempering | 1241 | 1172 | 1579 | 1655 | 0.280 |
| Aluminum 2024-T3 | 469 | 379 | 455 | 558 | 0.212 |
| 30CrMnSiA, ① Hardening and tempering | 1177 | 1104.5 | 1475.76 | 1795.1 | 0.215 |
| LC4CS, ① Heat treatment-CS | 613.9 | 570.8 | 775.05 | 710.62 | 0.379 |
| 40Cr ③ | 940 | 805 | 1592 | 1305 | 0.474 |
| 60Si2Mn, quench, medium-temperature tempering ③ | 1504.8 | 1369 | 1721 | 2172.4 | 0.20 |
| QT800-2, ② normalizing | 913 | 584.3 | 1777 | 946.8 | 1.121 |
| QT600-2, (B), ② normalizing | 748.4 | 456.5 | 1440 | 856.5 | 0.90 |
| QT600-2, (A) ② normalizing | 677 | 521.3 | 1622 | 888.8 | 1.06 |
| ZG35 ② normalizing | 572.3 | 366.3 | 1218 | 809.4 | 0.721 |
Note: 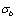 is a strength limit;
is a strength limit; 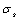 is an yield limit;
is an yield limit;
(A)-Bar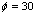 ; (B)-Y-type test specimen;
; (B)-Y-type test specimen;
①---The Masing’s materials; ②---The cycle-harden material ③-Cyclic softening.
4. Calculating Example
A test specimen made of nodular cast iron, its strength limit 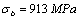 , yield limit
, yield limit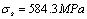 , its material constant
, its material constant 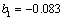 , the strength coefficient
, the strength coefficient 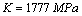 , fracture stress
, fracture stress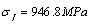 . To suppose the working stress
. To suppose the working stress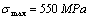 , the y(a/b)=1 when it is calculated in a design for the material, to try to calculate respectively following data:
, the y(a/b)=1 when it is calculated in a design for the material, to try to calculate respectively following data:
(1) Calculate the damage value 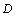 , the threseld value of damage, the critical value
, the threseld value of damage, the critical value 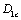 and the
and the 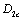 of damage for the material, respectivaly;
of damage for the material, respectivaly;
(2) Calculate the the 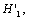 threshold factor
threshold factor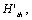
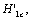 critical factors
critical factors 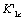 and
and 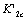 of damage, respectivaly;
of damage, respectivaly;
(3) To use the assessment method of the damage factor to do an assessment for it.
The processes and steps of calculations are as below.
(1) Calculate each critical value 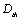 ,
,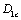 and
and 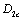 of damage, and to do an assessment for the material
of damage, and to do an assessment for the material
According to the formulas (8) and (1) their damage and threshold values in the first stage are calculated respectively as below,
Here 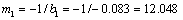
1). 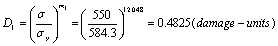
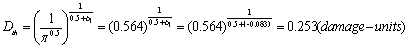 ;
;
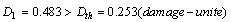
So the damage in the material is necessarily to grow.
According to the formula (13) its critical value of damage at the first stage is
2). According to the formula (14), its value of macro damage in the second stage is
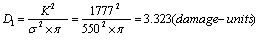 ;
;
3). By the formula (13), its critical value of macro damage is as below
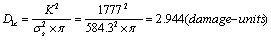 ;
;
So that 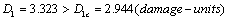
4). According to the formula (17), its critical value of momentary fracture is
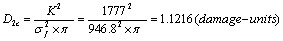 .
.
(2) Calculate the stress intensity factor 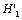 and the critical value
and the critical value 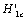 of damage in the first stage, respectivaly;
of damage in the first stage, respectivaly;
Its stress factor of damage in the first stage is
According to the formula (6) and (7), the factor 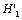 is
is
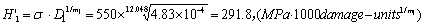 .
.
The critical factor of damage in the first stage is as below,
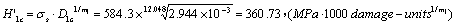 .
.
Its permited value should be,
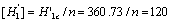
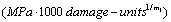 .
.
So that 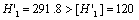
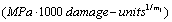 ,
,
Therefore, the calculating result by the criterion in the first stage, that is not safe.
(3) Calculate the stress intensity factor 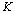 and the critical value
and the critical value 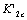 by macro damage, respectivaly;
by macro damage, respectivaly;
1). According to the formulas (9) ~ (12), the factor 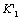 , the threshold value corresponding the yield stress
, the threshold value corresponding the yield stress 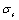 and the critical one of damage in second stage are respectively as follow,
and the critical one of damage in second stage are respectively as follow,
a) For the stress factors 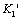 of the damage, here there are tow of calculating data, that are as follow,
of the damage, here there are tow of calculating data, that are as follow,
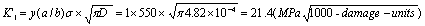
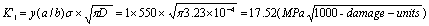 .
.
In two of calculating data, it should take larger one.
b). The threshold values 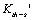 of the damage corresponding to the yield stress is as below
of the damage corresponding to the yield stress is as below
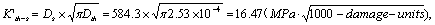
So 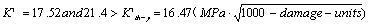 .
.
On the other hand, the critical factor on macro damage is
c). The critical factor of damage in this stage is
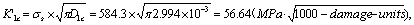
Its permited value should be,
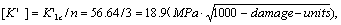
So that, the 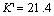 mentioned above, it is already greater than the permited value [K’],
mentioned above, it is already greater than the permited value [K’],

Therefore, the result calculated by the criterion on macro-damage, that is still not safe.
2) The critical factor in second stage is as below:
According to the strength criterion (15-16), the critical value of the momentary fracture is
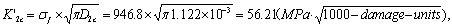
3) Its permissible value of damage factor is
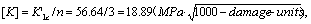
The result is also as bellowing case,` 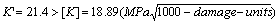
So that the damage value for the material is not in range of the permissible value for a design.
It can see from the above calculations, for the critical factors of damage, the 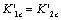 , because corresponding to end point of the
, because corresponding to end point of the 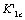 -value just is the starting point of the
-value just is the starting point of the 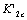 -value where they are at same point A2 on abscissa axis O4 IV; but for their critical values of damages,
-value where they are at same point A2 on abscissa axis O4 IV; but for their critical values of damages, 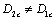 . So when to take the value for the
. So when to take the value for the 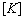 it must only be caculated by the
it must only be caculated by the 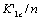 or
or 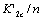 with the safe factor
with the safe factor 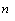 .
.
5. Conclusions
(1) The new threshold value of damage which it can show own inherent property, that is depended on the sole material constant b1, is a calculable one.
(2) For some materials of the brittle and happened strain hardening under monotonous loading, their critical damage values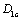 in the first stage could be calculated with corresponded the yield stresses
in the first stage could be calculated with corresponded the yield stresses 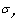 ; their critical values
; their critical values 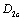 of the momentary fracture in the secodt stage could also be calculated with related the fracture stresses
of the momentary fracture in the secodt stage could also be calculated with related the fracture stresses 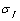 .
.
(3) The critical 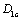 and
and 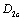 of damage are inherent constants shown the materials’characters; so the critical stress factors
of damage are inherent constants shown the materials’characters; so the critical stress factors 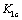 and
and 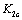 based on and
based on and 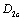 are also sole values, and are all calculable ones; Their computing models can be used to calculate both for the safe assessment to materials preexistted a flaw and for the predicting damage in design process; But the error of calculating data is larger for the shown strain softening’s ones.
are also sole values, and are all calculable ones; Their computing models can be used to calculate both for the safe assessment to materials preexistted a flaw and for the predicting damage in design process; But the error of calculating data is larger for the shown strain softening’s ones.
(4) Because the yield stresses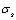 is the constant of uniquenesses for a material, the critical values of the damage
is the constant of uniquenesses for a material, the critical values of the damage 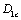 and the factor
and the factor 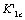 related the
related the 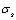 should also be considered as the only ones, and can also be applied as an important parameters showed its property; And for some cast iron, brittleness and low toughness materials, which are all the more so.
should also be considered as the only ones, and can also be applied as an important parameters showed its property; And for some cast iron, brittleness and low toughness materials, which are all the more so.
(5) The factor-value at end point of the 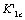 is the very one at starting point of the
is the very one at starting point of the 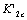 ; but for their critical values of damages,
; but for their critical values of damages, 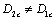 . So for some materials of the brittle and happened strain harding, if to take the value for the
. So for some materials of the brittle and happened strain harding, if to take the value for the 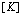 it must only be caculated by the
it must only be caculated by the 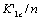 or
or 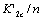 with the safe factor
with the safe factor 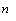 .
.
(6) In those computing models are proposed in the paper, if readers want to apply in engineering calculations, it must yet be verified by combined experiments, and it have to consider the influences for the shape and the size to a crack and a structure.
Acknowledgments
Author thanks sincerity the Zhejiang Guangxin New Technology Application Academy of Electromechanical and Chemical Engineering gives to support and provides research funds.
References
- Yan Gui Yu. Damage Growth Rate Calculations Realized in Whole Process with Two Kinks of Methods. American Journal of Science and Technology. Vol. 2, No. 4, 2015, pp. 146-164.
- Yangui Yu. The Life Predicting Calculations in Whole Process Realized from Micro to Macro Damage with Conventional Materials Constants. American Journal of Science and Technology.Vol. 1, No. 5, 2014, pp. 310-328.
- Yangui Yu. Life Predictions Based on Calculable Materials Constants from Micro to Macro Fatigue Damage Processes. American Journal of Materials Research. Vol. 1, No. 4, 2014, pp. 59-73.
- Yangui Yu. The Life Predicting Calculations Based on Conventional Material Constants from Short Crack to Long Crack Growth Process. International Journal of Materials Science and Applications. Vol. 4, No. 3, 2015, pp. 173-188. doi: 10.11648/j.ijmsa.20150403.15.
- Yangui Yu. The Life Predicting Calculations in Whole Process Realized with Two kinks of Methods by means of Conventional Materials Constants under Low Cycle Fatigue Loading. Journal of Multidisciplinary Engineering Science and Technology (JMEST) ISSN: 3159-0040 Vol. 1 Issue 5, December – 2014.
- Yangui Yu. Calculations for Crack Growth Rate in Whole Process Realized with Two Kinks of Methods for Elastic-Plastic Materials Contained Crack. Journal of Materials Sciences and Applications. Vol. 1, No. 3, 2015, pp. 100-113.
- Yangui Yu. The Life Predicting Calculations in Whole Process Realized by Calculable Materials Constants from short Crack to Long Crack Growth Process. International Journal of Materials Science and Applications. Vol. 4, No. 2, 2015, pp. 83-95. doi: 10.11648/j.ijmsa.20150402.13.
- Yangui Yu. The Calculations of Crack Propagation Rate in Whole Process Realized with Conventional Material Constants. Engineering and Technology. Vol. 2, No. 3, 2015, pp. 146-158.
- Yangui Yu. Calculations for Crack Growth Rate in Whole Process Realized with the Single Stress-Strain-Parameter Method for Elastic-Plastic Materials Contained Crack. <AASCIT> Journal of Materials Sciences and Applications. Vol. 1, No. 3, 2015, pp. 98-106.
- Yu Yangui, Sun Yiming, MaYanghui and XuFeng. The Computing of intersecting relations for its Strength Problem on Damage and Fracture to Materials with short and long crack, In: International Scholarly Research Network ISRN. Mechanical Engineering, Volume, Article ID 876396. http://www.hindawi.com/isrn/me/(2011).
- David Broek Elementary Engineering Fracture Mechanics, Third revised edition Martinus Nijhoff Publishers, 1982, 6~14.
- Michael F. Ashby and David R. H. Jones, Engineering Materials, An introduction to their propertied and applications, Pergamon Press, 1980, P. 145-147.
- B. P. Kogaev, H. A. Maxymov, A. P. Gycenkov. Calculations on Strength and Durability for the Structure and Mechanical parts, Handbook, Machinery Industry Press, Moscow, 1985 70~75. (in Russian) (B.П. Koгaeв, H. A. Maxymoв, A. П. Гyceнкoв. Pасчеты Деталей Mашин и Kонструкций на Прочность и долговечность, Cправочник, Машиностроение 1985, Москва, 70-75).
- China Machine Press, Mechanical design handbook, New Edition, Volume 5.31-124-135; 31-57-60; 31-134-136.(in Chinese).
- Shaobian Zhao and Zhongbao Wang, Anti-Fatigue Design---Methods & Data, China Machine Press, P. 90-109, 469-489.
- Yangui Yu. Multi-Targets Calculations Realized for Components Produced Cracks with Conventional Material Constants under Complex Stress States. <AASCIT> Engineering and Technology. Vol. 3, No. 1, 2016, pp. 30-46.
- Yangui Yu. The Calculations of Evolving Rates Realized with Two of Type Variables in Whole Process for Elastic-Plastic Materials Behaviors under Unsymmetrical Cycle. Mechanical Engineering Research. Canadian Center of Science and Education 2012; 2. (2): 77-87; ISSN 1927-0607 (print) E-ISSN 1927-0615 (Online).
- Yangui Yu, The life predictions in whole process realized with different variables and conventional materials constants for elastic-plastic materials behaviors under unsymmetrical cycle loading, Journal of Mechanics Engineering and Automation. 5 (2015) 241-250. doi: 10.17265/2159-5275/2015.04.006.
- Yangui Yu. The Predicting Calculations for Lifetime in Whole Process Realized with Two Kinks of Methods for Elastic-Plastic Materials Contained Crack. <AASCIT> Journal of Materials Sciences and Applications. Vol. 1, No. 2, 2015, pp. 15-32.
- S. V. Doronin, et al., Ed. RAN U. E. Soken, Models on the fracture and the strength on technology systems for carry structures, (Novosirsk Science, 2005), PP. 160-165.(in Russian).
- U. Zerbst, S. Beretta, G. Kohler, A. Lawton, M. Vormwald, H. Th. Beier, C. Klinger, I. C erny´, J. Rudlin, T. Heckel a, D. Klingbeil, Safe life and damage tolerance aspects of railway axles – A review. Engineering Fracture Mechanics. 98, 214–271 (2013).