| 1. | ||
| 2. | ||
| 3. | ||
| 4. | ||
| 5. | ||
On Galois Groups
Faisal Hussain Nesayef
Department of Mathematics, Faculty of Science, University of Kirkuk, Kirkuk, Iraq
Email address
Citation
Faisal Hussain Nesayef. On Galois Groups. American Journal of Science and Technology. Vol. 3, No. 1, 2016, pp. 43-46.
Abstract
Galois Theory is one of the interesting subjects in Mathematics. It constitutes a link between Polynomials, Fields and Groups. This paper considers manipulation of polynomials, studies and investigates some applications of groups and Fields and their extensions. Polynomials are regarded as an essential tools in the construction of rings and fields. Consequently the ring theory plays the basic role in the study of Galois groups, particular attention has been given to the algebraic polynomials, in terms of their reducible or irreducible properties. This has led to the study of Fields, Extension Fields and the Galois groups. The subject was extensively studied by the great mathematician Galois first. Subsequently many other mathematicians contributed in this field, appreciating Galois' great achievement in this area of mathematics.
Keywords
Basis, Extension Fields, Galois Group, Irreducible Polynomials, Minimal Polynomial, Monic Polynomial, Splitting Fields, Transcendental
1. Introduction
In this paper some properties have been studied in order to find out about the basic relationships between the fields, rings and polynomials. Some results have been stated and used from [1], [2], [3] and [4]. The main objective of this paper is to investigate the Automorphisms of the field extensions.
In section one, the basic principles and properties have been covered in order to make the consequent progress as smooth as possible.
Section two deals with the basic properties of the polynomial rings, the nature and the structure of the extension fields.
Section three tackles some important results discovered by many other researchers.
Section four deals with some applications of the Galois Groups, their nature, and their structural properties and characteristics.
The conclusion of this paper is to investigate the relationship between the roots of unity and the Galois Groups Gal (
). Also to prove that for 
and 
, the Galois group will not be necessary abelian.
2. Basics
In this section we cover the basic terminologies required as a background knowledge in the latter sections. These are mainly given in other reference, such as [1], [2], etc.
Definition 1.1: Let F be a field. Then F[x] denotes the ring of polynomials with coefficients in F. i.e. 
Where 
, where 
.
Let f and g be polynomials in F[x], with 
. Then there exist polynomials 
such that 
where either r = 0 or 
Definition 1.2: Let f, g, h be polynomials in F(x). Then g divides f, ie (g | f) if there exists 
such that f = q g.
The polynomial f is reducible if it is non-constant and whenever we have factorization
f = g h, either g or h is a unit. In this case
Proposition 1.3: Suppose 
where 
are co-prime is a root of 
Then 
and 
Proof
Since r divides each term in this expression, then 
.
Also r and s are co-prime, therefore . Also 
and since r and s are co-primes, then s divides
.
Example 1: let 
Then the only possible roots are 
Therefore f is irreducible.
Definition 1.3: A field is a set F with two binary operations "+" and "." such that
(a) 
is a commutative group
(b) (
is a commutative group, where 
(c) The distribution law holds.
An example of a field is Q[√2]. The set of all numbers which can be written a+b√2 for a and b rational numbers.
Definition (Algebraic Number): f α is a real number with the property that p(α)=0 for some polynomial p(x), then we say that α is an algebraic number.
If α is an algebraic number then Q[α] is a field. Q[α] consists the set of elements of the form a0+a1α+…+an−1αn−1 where each ai is a rational number and n is the smallest integer such that there is a polynomial p(x) of degree n with p(α)=0. Q[α] is the smallest field extension of Q containing α. Q[2√3]={a+b2√3+c2√3.2:a,b,c ∈ Q} is another example of a field. This idea can be extended to define, for α, β both algebraic, Q[α,β] to be the set of all expressions like 2αβ, α+α2β, and so on. [√2,√3]={a+b√2+c√3+d√6: a, b, c, d ∈Q} is an example of a Field.
The characteristic of a field
Definition 1.4: A field F is of finite characteristic p (Char (F) = p) if there is a least positive integer p such that (1+1+1+…+1) = 0 in F, (p-times). If there is no such integer, then F is said to have characteristic 0.
3. Extension Fields
Definition 2.1: Let F be a field. A field extension of F is a field E containing F. We write E/F as a field extension. E.g. C/R, Q/Q, Q
/ Q
If E is a field containing F then, for all 
, then product 
is defined in E ; thus we have a scalar multiplication by F on E. Looking at the axioms for E to be a vector space over F, we see that they are all special cases of the axioms for E to be a field. Hence E is indeed a vector space over F and it has a basis and dimension over F.
Definition 2.2: Let E/F be a field extension. If E is finite dimensional as a vector space over F then we say that E/F is a finite extension, otherwise it is infinite. If it is finite then the degree of E/F is 
.
For example, in the extensions above we have:
• 
is finite of degree [
] = 2, because {1,i} is a basic for 
as a 
-vector space.
• 
is finite;
• is finite of degree [
]=1, because { q } is a basis for any 
;
• 
is finite of degree 2, because B = {1,
} is a basis. In this case it is clear that B spans 
, since 
. To see that B is linearly independent over 
, suppose 
for some 
.
If 
then 
which is absurd. Hence b = 0 and so a = 0.
Algebraic extensions
Definition 2.3: Let E/F be a field extension and 
is algebraic over F if there is a non-zero polynomial 
such that 
; otherwise 
is transcendental over F.
Splitting Fields
Definition 2.4: Let F be a field, let
and let E/F be an extension.
(i) We say that f splits over E if it factorizes completely in E[x], i.e it can be expressed as a product of linear factors
(ii) We say that E is a splitting field for f over F if f splits over E but not over any intermediate extension 
.
Remark: If f splits over E as above, then we can describe a splitting filed for f over F quite easily. 
is the subfield of E of rational functions in 
with coefficients in F (equivalently, it is the smallest subfield of E containing F and
). Inductively we can define:
, since E is a field extension of 
, then 
is the smallest field containing F and all the root 
of f. So it is a splitting for f over F.
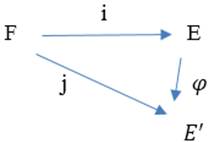
Figure (1). Isomorphism of two splitting fields E and 
of the field F.
Theorem 2.5: Let F be a field and 
a polynomial of degree n. Then there exists a splitting filed E for f over F, and 
Moreover if 
is another splitting filed for f over F then E is isomorphic to as extensions of F, i.e. there is an isomorphism 
such that the following diagram commutes: That is, 
Proof of existence. By the remark above. It is sufficient to find an extension of degree at most n!, in which f splits. We proceed by induction on n, noting that when n = 1 the polynomial f already factorizes over F and [F:F] = 1. So we turn to the inductive step and start by factorizing f over F,
where each 
is irreducible in F[x] and 
Put 
, an extension of F of degree 
which contains a root of 
. Since is also a root of f, we can factorize
Now 
so we can apply the inductive hypothesis to find an extension E of 
of degree at most (n-1)!, in which
splits. Then f also splits in E and by the Tower Law
, as required
To prove the uniqueness we consider the following example:
Example 2: Find the degree of the splitting field of 
Solution: we have to factorize the polynomial first. We have 
and the second factor is irreducible as the only possible roots are 
but neither is a root.
Let 
be a root of 
then 
is a splitting field, since 
and 
, since w has minimal polynomial 
of degree 2.
Normality
Definition 2.6: finite extension E/F is normal if any irreducible polynomial 
which has a root in E splits completely over E.
Note that normality is a property of the extension not of the field. Also note that, to show that an extension E/F is not normal, we need only find an irreducible polynomial in F[X] which has a root in E but does not split over E. On the other hand, to prove that an extension is normal, we need the following proposition which is stated in [4].
Proposition 2.7 Finite extension E/F is normal if and only if it is the splitting field over F of some polynomial in F[X].
Example 3:
(i) 
) is not a normal extension of : the irreducible polynomial 
has a root 
in 
but does not split in , since the other roots of f in are not real.
(ii) 
) is a normal extension of ; since we have seen that it is the splitting field over of 
.
(iii) 
) is a normal extension of ; since it is the splitting field over of 
.
4. Galois Theory
Automorphisms of field extensions
Definition 4.1 Let 
be a field extension. An 
is an isomorphism 
such that 
. We write Aut 
for the set of 
of 
.
Note that Aut is actually a group, with composition:
• If 
Aut 
then so is 
It is certainly an isomorphism from to itself, where 
.
• The map 
given by 
for all 
is the identity element of Aut.
• If 
Aut
then 
Aut as 
for 
Example 4 Let 
be a polynomial, then:
(a) The splitting field of p(x) is Q[
].(b) The automorphisms of p(x), which are the symmetries of the roots, are given by: f (a + b
) = a−b
and g (x) = x.
Lemma 4.2 Let 
be a field extension. Let 
be algebraic over F, and let 
Aut
. Then 
is a root of the minimal polynomial of 
over F.
Proof: Let 
be the minimal polynomial over F of 
Then
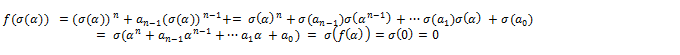
Let 
of F. Then
• Any 
Aut
must map each 
to a root of its minimal polynomial over 
.
• Aut is uniquely determined by specifying 
in terms of 
and elements of F, while 
is a homomorphism.
Example 5:
(i) Aut
has at most two elements, since 
must be mapped to either 
(as these are the roots of 
the minimal polynomial of 
over ), and specifying which one of these occurs determines the automorphism. Indeed, there are two: the identity map i, and the map given by: 
(ii) Aut
has only the identity map, as 
has minimal polynomial 
over , whose only root in is 
and hence 
can only be mapped to itself.
Example 6 For each of the following polynomial 
, we find a splitting field E over , the Galois group of 
over , and all intermediate fields: 
We also, identify those subfields for which 
is Galois and in that case, find Gal(L/).
The splitting field is E = 
, where 
, since the roots of 
are 
. This has degree 8 over 
so writing G = Gal (E / 
. We have 
Any automorphism is uniquely determind by its action on 
and i. It it must map I to 
and to one of the roots of 
Hence there are 8 possible automorphims. Hence there are automorphisms 
such that:
. Then we can easily check that 
.
This is a dihedral group with 8 elements,
Remark Since 
is a subgroup of 
, we could ask to identify it as such. Numbering the roots 
as 1,2,3,4 respectively, we see that 
and G ={1, (1234), (13)(24), (1432), (24), (14)(23), (13), (12)(34)}.
Example 7. Let 
be a polynomial, then 
, where,
g is the identity element of the group and 
, as
This group is cyclic of order 2 isomorphic to 
.
5. Applications
We are now going to introduce some results about application of Galois Group.
Proposition 5.1 Let F be a field with char 
Suppose P is an odd prime. There exists a field (up to homomorphism) with 
elements.
Proof Take a field of characteristic p. K contains 
. So consider the quadratic extension 
. Define a homomorphism
by 
. Then ker (
.
Therefore 
has index two in 
so is the only possible field which can be 
.
Proposition 5.2 Let G be the Galois group of the polynomial 
over Q, show that 
Proof: The splitting field Q[
], where 
and 
. This is generated by 
where 
and 
. So the group has order 20.
Proposition 5.3
Every field homomorphism 
must be one – to –one and onto.
Proof: 
acts as the identity map on 
and . 
. Therefore preserver the order Therefore if 
we have 
resulting in 
Theorem 5.4 If 
a primitive 
root of unity is , with 
, then Gal(
) is abelian of deg. at most n - 1.
Proof: Since 
is a root of 
and 
the minimal polynomial of and has degree at most n - 1.
Also the roots of 
are 
which are all in 
.
So this is the splitting field of and so it is a Galois extension.
Let 
/
is gives by 
for some 
.
Since 
is a root of ,
Therefore 
. Therefore 
.
Theorem 5.5 Let
and 
. Then the Galois group of Q is not necessarily abelian.
Proof: Let 
the splitting field of 
over
If 
and 
then the root of 
in C are: 
Take 
. Put 
the splitting field over of , then we have 
Let 
and 
. The subgroup of G with respect to the intermediate field K.
Since K/Q is normal, then N is a normal subgroup of G and 
.
Also 
is abelian by theorem 5.4.
References
