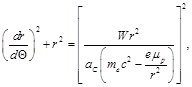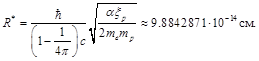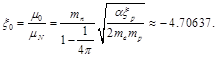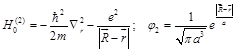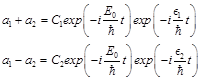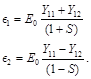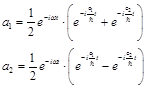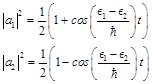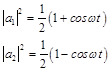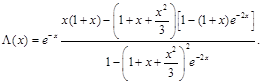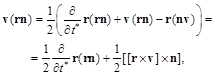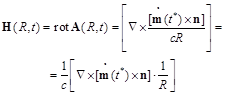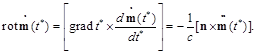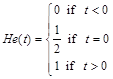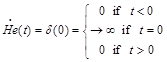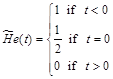1.2. The Electromagnetic Model of Neutron
For the first time after the discovery of the neutron, physicists was discussing whether or not to consider it as an elementary particle.
Experimental data, which could help to solve this problem, was not exist then.
And soon the opinion was formed that the neutron is an elementary particle alike proton [3].
However, the fact that the neutron is unstable and decays into a proton and an electron (+ antineutrino) gives a reason to consider it as a non-elementary composite particle.
Is it possible to now on the basis of experimentally studied properties of the neutron to conclude that it is elementary particle or it is not?
Let's consider the composite corpuscle, in which electron is spinning around proton with speed v→c. At that it has mass me and charge -e.
The presence of the intrinsic magnetic moment of the rotating particle does not matter because of the particularities of the resulting solutions Eq. (18).
Between the positively charged proton and negatively charged electron there must be a force Coulomb attraction:
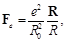 (3)
(3)
It is caused by existing of the Coulomb interaction energy:
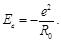 (4)
(4)
Where R0 is the radius of an orbit of the rotating particle.
The magnetic field generated by the electron orbital motion creates a force which is opposing to the Coulomb force and tends to break the orbit.
According to the Biot-Savart law an element of orbit dl with the current J creates at a distance R the magnetic field:
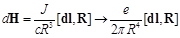 (5)
(5)
The force acting on an element coil dl and tending to rend the coil is
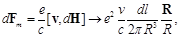 (6)
(6)
the entire coil will rupture by the force
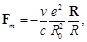 (7)
(7)
The action of this force at v → c balances the Coulomb attraction.
Integrating Eq. (6), we find that the element coil dl acquires the energy
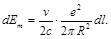 (8)
(8)
At thus as it follows from Eq. (8), the energy of ring tearing at v → c will tend to
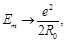 (9)
(9)
that together with the Coulomb energy Eq. (4) will provide the steady-state of the current ring.
As the result, the Coulomb force and the magnetic force will be compensated.
Only the Lorentz's force arising from the interaction of a moving charged electron and magnetic moment of the proton μp remains uncompensated.
An observer moving in a magnetic field H′y "sees" in his reference system an electric field ([4], §24, Eq. (24.2)):
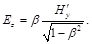 (10)
(10)
Where β = v / c.
The Lorentz force conforming to this field is:
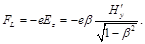 (11)
(11)
If the rotation is in the plane of the "equator" of the proton, the magnetic field is:
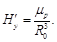 (12)
(12)
In equilibrium, the Lorentz force is balanced by the centrifugal force:
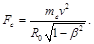 (13)
(13)
That allows us to determine the radius of the electron equilibrium orbit (at v → c)
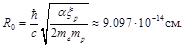 (14)
(14)
Where α = e2 / ħc is the fine structure constant, ξp is the anomalous moment of proton, me and mp are masses of electron and proton (in the rest).
1.3. Spin of the Current Ring
The angular momentum (spin) of the current ring
S0 = [p0, R0] (15)
is created by the generalized momentum of electron
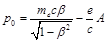 (16)
(16)
and depends on the magnetic moment of the proton
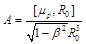 (17)
(17)
After the substitution of value of the vector-potential A from Eq.(17) and the value of radius of current ring R0 from Eq.(14) to Eq.(16), at v → c we obtain p → 0 and respectively
S0 = 0. (18)
In this connection it is unimportant, has the rotating particle an own magnetic moment or not.
At zero spin, there is no direction for its orientation.
1.4. Accounting for the Effect of the Precession of the Orbit
The rotation of the electron must be characterized by two integrals of motion.
At this moving, the energy of rotating particle W and its moment of rotation K must be kept constant.
If v → c, one can write
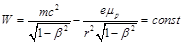 (19)
(19)
and
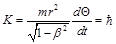 (20)
(20)
Where β = v / c and
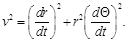 (21)
(21)
If to remove β and t from these equations, we obtain:
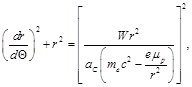 (22)
(22)
where aC = ħ / mec is the Compton radius.
After replacing of variable
u = 1 / r (23)
and taking the derivative d /dΘ, we obtain
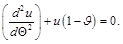 (24)
(24)
There we take into account that the derivative
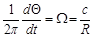
is the angular velocity of the particle rotation and we indicate ϑ = 1 / 2π.
The solution of the equation
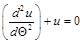 (25)
(25)
is the ellipse
u = const (1 + ε cos Θ) (26)
The Eq. (24) describes the "almost", elliptical trajectory, which precesses around the proton:
per revolution of the electron, the orbit rotates on π·ϑ [5].
Thus, this precession of the ellipse with the frequency ω is superimposed on the rotation of the particle on the elliptical orbit with the frequency Ω:
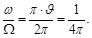 (27)
(27)
To take into account the effect of this precession, instead of Eq. (14), we introduce the effective radius R*.
Due to the fact that this radius is determined by the ratio of universal constants only, it can be calculated with a very high accuracy:
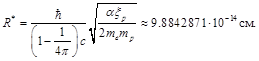 (28)
(28)
1.5. The Magnetic Moment of the Neutron
Attempts to calculate the magnetic moment of the neutron have been made before [6, 7].
In the frame of the constructed electromagnetic model, the neutron magnetic moment can be calculated with very high accuracy.
The current J in a ring with radius R0 creates a magnetic moment that is proportional to the square of the ring:
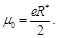 (29)
(29)
We can rewrite it in units of nuclear Bohr magneton (μN = eħ / 2cmn, where mn is neutron mass).
In these units the magnetic moment of the ring is equil to
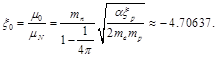 (30)
(30)
The resulting magnetic moment of the neutron is equal to the sum of the proton magnetic moment and the magnetic moment of the ring:
ξn = ξp + ξ0 = 2.79285 – 4.70637 ≈ – 1.91352, (31)
that very well agrees with the measured value of the magnetic moment of the neutron Eq. (2):
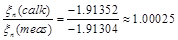 (32)
(32)
1.6. The Energy of Neutron Decay
The depending on the relativistic factor (1 – v2/c2) –1/2 terms of energy of the current ring form the integral of motion Eq. (19).
At substituting in Eq. (19) of the obtained value of the equilibrium orbit radius r = R0, we can easily see that at equilibrium the relativistic terms of energy balance each other and W=0.
At the same time the Coulomb energy of the ring (Eq. (4)) and its magnetic energy (Eq. (9)) are independent on the relativistic coefficient (1 – v2/c2) –1/2. Their sum is not equal to zero:
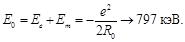 (33)
(33)
At the decay of a neutron, this energy must go into the kinetic energy of the emitted electron (and antineutrinos). That is in quite satisfactory agreement with the experimentally determined boundary of the spectrum of the decay electrons, equal to 782 keV.
1.7. The Mass of Neutron
The kinetic energy of a relativistic particle in the general case can be written as [4]:
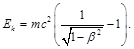 (34)
(34)
The maximum kinetic energy of electron produced in the decay of neutron was calculated above (Eq. (33)).
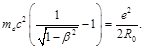 (35)
(35)
It follows from this equation that the mass of relativistic electron
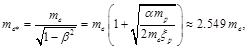 (36)
(36)
where me is mass of electron in the rest.
It is important that the sum of the masses of proton and relativistic electron in very good agreement with the measured value of the mass of the neutron (1):
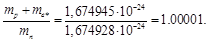 (37)
(37)
1.8. Discussion
This consent of estimates and measured data indicates that the neutron is not an elementary particle. It should be seen as a some relativistic analog of the Bohr hydrogen atom. With the difference: a non-relativistic electron in the Bohr atom forms a shell by means of Coulomb forces and in a neutron the relativistic electron is held by the magnetic interaction [8].
This must change our approach to the problem of nucleon-nucleon scattering. The nuclear part of an amplitude of the nucleon-nucleon scattering should be the same at all cases, because in fact it is always proton-proton scattering (the only difference is the presence or absence of the Coulomb scattering). It creates the justification for hypothesis of charge independence of the nucleon-nucleon interaction.
According to the principle which was developed by W. Gilbert and G. Galileo more than 400 years ago, a theoretical construct can be attributed to reliably established if it is confirmed by experimental data.
This principle is the basis of modern physics and therefore the measurement confirmation for the discussed above electromagnetic model of neutron is the most important, required and completely sufficient argument of its credibility.
Nevertheless, it is important for the understanding of the model to use the standard theoretical apparatus at its construction.
It should be noted that for the scientists who are accustomed to the language of relativistic quantum physics, the methodology used for the above estimates does not contribute to the perception of the results at a superficial glance.
It is commonly thought that for the reliability, a consideration of an affection of relativism on the electron behavior in the Coulomb field should be carried out within the Dirac theory.
However that is not necessary in the case of calculating of the magnetic moment of the neutron and its decay energy.
In this case, all relativistic effects described by the terms with coefficients (1 – v2/c2) –1/2 compensate each other and completely fall out.
The neutron considered in our model is the quantum object. Its radius R0 is proportional to the Planck constant ħ.
But it can not be considered as relativistic particle, because coefficient (1 – v2/c2) –1/2 is not included in the definition of R0.
In the particular case of the calculation of the magnetic moment of the neutron and the energy of its decay, it allows to find an equilibrium of the system from the balance of forces, as it can be made in the case of non-relativistic objects.
The another case exits at the evaluation of the neutron lifetime. The relativism affects on this parameter apparently and one can not obtain even a correct estimation of the order of its value.
2. About Nature of Nuclear Forces
2.1. The One-Electron Bond Between Two Protons
Let us consider a quantum system consisting of two protons and one electron.
If protons are separated by a large distance, this system consists of a hydrogen atom and the proton.
If the hydrogen atom is at the origin, then the operator of energy and wave function of the ground state have the form:
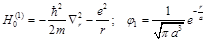 (38)
(38)
If hydrogen is at point R, then respectively
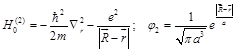 (39)
(39)
In the assumption of fixed protons, the Hamiltonian of the total system has the form:
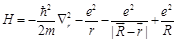 (40)
(40)
At that if one proton removed on infinity, then the energy of the system is equal to the energy of the ground state E0, and the wave function satisfies the stationary Schrodinger equation:
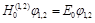 (41)
(41)
We seek a zero-approximation solution in the form of a linear combination of basis functions:
ψ = a1 (t) φ1 + a2 (t) φ2 , (42)
where coefficients a1 (t) and a2 (t) are functions of time, and the desired function satisfies to the energy-dependent Schrodinger equation:
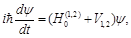 (43)
(43)
where V1,2 is the Coulomb energy of the system in one of two cases.
Hence, using the standard procedure of transformation, we obtain the system of equations
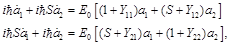 (44)
(44)
where we have introduced the notation of the overlap integral of the wave functions
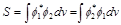 (45)
(45)
and notations of matrix elements
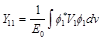
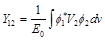 (46)
(46)
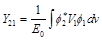
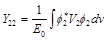
Given the symmetry
Y11 = Y22; Y12 = Y21 , (47)
after the adding and the subtracting of equations of the system (44), we obtain the system of equations
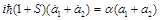
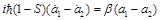 (48)
(48)
Where
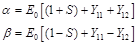 (49)
(49)
As a result, we get two solutions
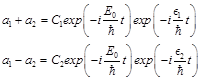 (50)
(50)
Where
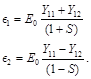 (51)
(51)
From here
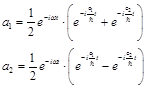 (52)
(52)
and
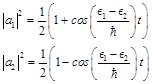 (53)
(53)
As
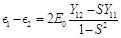 (54)
(54)
with the initial conditions
a1(0) = 1; a2(0) = 0 (55)
and
C1 = C2 = 1 (56)
or
C1 = – C2 = 1 (57)
we obtain the oscillating probability of placing of electron near one or other proton:
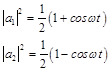 (58)
(58)
Thus, electron jumps into degenerate system (hydrogen + proton) with frequency ω from one proton to another.
In terms of energy, the frequency ω corresponds to the energy of the tunnel splitting arising due to electron jumping (Fig. 1).
As a result, due to the electron exchange, the mutual attraction arises between protons. It decreases their energy on
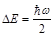 (59)
(59)
The arising attraction between protons is a purely quantum effect, it does not exist in classical physics.
The tunnel splitting (and the energy of mutual attraction between protons) depends on two parameters:
Δ = |E0|·Λ(x), (60)
where E0 is energy of the unperturbed state of the system (ie, the electron energy at its association with one of proton, when the second proton removed on infinity), and function of the mutual distance between the protons Λ(x).
This dependence according to Eq. (54) has the form:
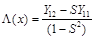 (61)
(61)
The graphic estimation of the exchange splitting ΔE indicates that this effect decreases exponentially with increasing a distance between the protons in full compliance with the laws of the particles passing through the tunnel barrier.
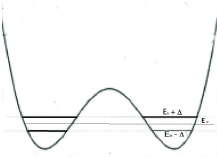
Fig. 1. The schematic representation of the potential well with two symmetric states. In the ground state, electron can be either in the right or in the left hole. In the unperturbed state, its wave functions are either 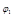 or
or 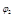 with the energy E0. The quantum tunneling transition from one state to another leads to the splitting of energy level and to the lowering of the sublevel on Δ.
with the energy E0. The quantum tunneling transition from one state to another leads to the splitting of energy level and to the lowering of the sublevel on Δ.
2.2. The Molecular Hydrogen Ion
The quantum-mechanical model of simplest molecule - the molecular hydrogen ion - was first formulated and solved by Walter Heitler and Fritz London in 1927 [9-11].
At that, they calculate the Coulomb integral
Y11 = 1 – (1 + x) e –2x, (62)
the integral of exchange
Y12 = x (1 + x) e – x (63)
and the overlap integral
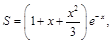 (64)
(64)
where x = R /aB is the dimensionless distance between the protons.
The potential energy of hydrogen atom
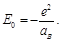 (65)
(65)
and with taking into account Eq. (62)-Eq. (64)
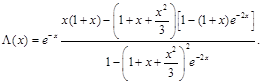 (66)
(66)
At varying the function Λ(x) we find that the energy of the system has a minimum at x ≈ 1.3 where Λ x = 1.3 ≈ 0.43.
As a result of permutations of these values we find that in this minimum energy the mutual attraction of protons reaches a maximum value
Δmax ≈ 9.3·10 –12 erg. (67)
This result agrees with measurements of only the order of magnitude.
The measurements indicate that the equilibrium distance between the protons in the molecular hydrogen ion x ≈ 2 and its breaking energy on proton and hydrogen atom is close to 4.3·10 –12 erg.
The remarkable manifestation of an attraction arising between the nuclei at electron exchange is showing himself in the molecular ion of helium.
The molecule He2 does not exist.
But a neutral helium atom together with a singly ionized atom can form a stable structure - the molecular ion.
The above obtained computational evaluation is in accordance with measurement as for both - hydrogen atom and helium atom - the radius of s-shells is equal to aB, the distance between the nuclei in the molecular ion of helium, as in case of the hydrogen molecular ion, must be near x ≈ 2 and its breaking energy near 4.1·10 –12 erg.
In order to achieve a better agreement between calculated results with measured data, researchers usually produce variation of the Schrodinger equation in the additional parameter- the charge of the electron cloud. At that, one can obtain the quite well consent of the calculations with experiment. But that is beyond the scope of our interest as we was needing the simple consideration of the effect.
2.3. Deuteron and Other Light Nuclei
2.3.1. Deuteron
According to this model, neutron is proton surrounded by a relativistic electron cloud.
Therefore a deuteron consists of the same particles as the molecular ion of hydrogen.
There is a difference. In the case of a deuteron, the relativistic electron cloud has the linear dimension R0 ≈ 10 –13 cm (Eq. (14)).
One might think that a feature occurs at such a small size of the electron cloud.
When an electron jumps from one proton to another, a spatial overlap of the wave functions will not arise and therefore the overlap integral S (Eq. (64)) can be set equal to zero.
In accordance with the virial theorem and Eq. (33), the potential energy of this system at the unperturbed state is
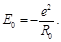 (68)
(68)
The function Λ(x) (Eq. (61)) at S=0 and taking into account Eq. (63) obtains the form
Λ(x) = x (1 + x) e – x, (69)
Where x = R /R0 is a dimensionless distance between the protons.
When varying this expression we find its maximum value Λmax = 0.84 at x = 1,62.
After substituting these values, we find that at the minimum energy of the system due to exchange of relativistic electron, two protons reduce their energy on
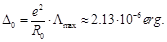 (70)
(70)
To compare this binding energy with the measurement data, let us calculate the mass defect of the three particles forming the deuteron
δmd = 2mp + me* – md ≈ 3.9685·10 –27 g, (71)
where md is is mass of deuteron.
This mass defect corresponds to the binding energy
Ed = δmd ·c2 = 3.567·10 –6 erg. (72)
Using the relativistic electron mass in Eq. (75) does not seem obvious.
However, this is confirmed by the fact that at the fusion reaction proton and neutron to form a deuteron
p + n → D + γ (73)
γ-quantum takes energy equal to 3.563·10 –6 erg [12-13].
Thus the quantum mechanical estimation of the bonding energy of deuteron Eq. (70), as in the case of the hydrogen molecular ion, consistent with the experimentally measured value Eq. (72), but their match is not very accurate.
Schematic representation of the structure of light nuclei. Dotted lines schematically indicate the possibility of a relativistic electron hopping between protons.
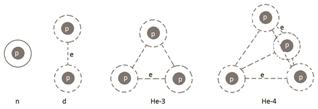
Fig. 2. Schematic representation of the structure of light nuclei.
Dotted lines schematically indicate the possibility of a relativistic electron hopping between protons.
2.3.2. Nucleus 32He
As can be seen from the schematic structure of this nucleus (Fig. 2), its binding energy is composed by three pairwise interacting protons. Therefore it can be assumed that it equals to the tripled energy of deuteron:
EHe3 = 3·Ed ≈ 10.70·10 –6 erg. (74)
The mass defect of this nucleus
Δm (He3) = 3mp + me* – mHe3 = 1.19369·10 –26 g. (75)
Thus mass defect corresponds to the binding energy
E (32He) = Δm (He3)·c2 ≈ 10.73·10 –6 erg. (76)
Consent energies EHe3 and E (32He) can be considered as very good.
2.3.3. Nucleus 42He
As can be seen from the schematic structure of this nucleus (Fig. 2), its binding energy is composed by six pairwise interacting protons which are realised by two electrons. On this reason its binding energy can be considered as:
EHe4 = 2·6·Ed ≈ 42.80·10 –6 erg. (77)
The mass defect of this nucleus
Δm (He4) = 4mp + 2me* – mHe4 = 48.62·10 –26 г. (78)
Thus mass defect corresponds to the binding energy
E (42He) = Δm (He4)·c2 ≈ 43.70·10 –6 erg. (79)
Consent of these energies can be considered as alright.
2.3.4. Nucleus 63Li
The binding energy of Li-6 can be represented by the sum of binding energy of He-4 and deuteron. The last placed on next shell and has a weak bounding with He-4:
E Li6 ≈ E He4 +·Ed ≈ 47.26·10 –6 erg. (80)
The mass defect of this nucleus
Δm (Li6) = 6mp + 3me* – mLi6 = 54.30·10 –26 g. (81)
and corresponding binding energy
E (63Li) = Δm (Li6)·c2 ≈ 48.80·10 –6 erg. (82)
That really confirms the weak link between the protons in different shells.
It should be noted that the situation with the other light nuclei are not so simple.
The nucleus 31T consists of three protons and two communicating electrons between them.
Jumps of two electrons in this system should obey to the Pauli exclusion principle.
Apparently this is the reason that the binding energy of tritium is not very much greater than the binding energy of He-3.
Nuclear binding energy of Li-7 can be represented as E Li7 ≈ E He4 + ET. But it is quite a rough estimate.
At that the binding energy of unstable nucleus Be-8 very precisely equal to twice binding energy of He-4.
2.4. Conclusion
The good agreement between the calculated binding energy of some light nuclei with measured data suggests that nuclear forces (at least in the case of these nuclei) have the above-described exchange character. These forces arise as a result of a purely quantum effect of exchange relativistic electrons.
For the first time the attention on the possibility of explaining the nuclear forces based on the effect of electron exchange apparently drew I. E. Tamm \cite{Tamm} back in the 30s of the last century.
However, later the model of the π-meson and gluon exchange becomes the dominant in nuclear physics. The reason for that is clear.
To explain the magnitude and range of the nuclear forces need particle with a small wavelength.
Non-relativistic electrons does not fit it.
However, on the other hand, the model π –meson or gluon exchange was not productive:
it gives not possibility to calculate the binding energy of even light nuclei.
Therefore, the simple assessment of the binding energy given above and consistent with measurements is the clear proof that the so-called strong interaction in the case of light nuclei is a manifestation of the quantum-mechanical effect of attraction between protons produced by the relativistic electron exchange.
3. Neutrinos
3.1. Electromagnetic Waves
The radiation and propagation of electromagnetic waves in vacuum is considered in detail in a number of monographs and textbooks. Taking as the basis for the consideration of these mechanisms the description given by the course of the Landau-Lifshitz [4], let us consider the mechanism of excitation and propagation of waves in vacuum in the absence of electric charges, electric dipoles and currents. A time variable magnetic dipole moment m will be the only source of electromagnetic fields in the following consideration.
3.1.1. The Vector Potential Generated by a Magnetic Dipole
In general, the potentials of the electromagnetic fields generated by electric charge distribution ρ and the current j at the point R with allowance for retardation, are written in the form:
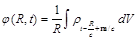 (83)
(83)
and
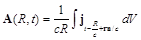 (84)
(84)
Where r is the radius-vector within the system of charges and currents, n = R / R is the unit vector.
Introducing the delayed time t* = t – R /c, we write down the first two terms of the expansion of the vector potential expression (84) in powers of rn /c:
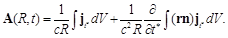 (85)
(85)
Using the definition j = ρv and passing to the point charges, we obtain:
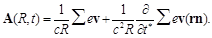 (86)
(86)
Due to the fact that the expression of the second term can be transformed to
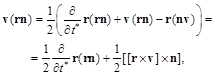 (87)
(87)
and using the definitions of the electric dipole d, the electric quadrupole moment Q and the magnetic dipole moment
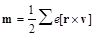 (88)
(88)
we obtain in accordance with ([4] Eq.71.3):
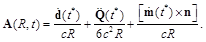 (89)
(89)
Where the first two terms describe the electric dipole and electric quadrupole radiation.
In our case, they are equal to zero, since there are no appropriate moments in the beginning condition of statement of the problem.
So finally for our case we have
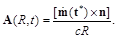 (90)
(90)
3.1.2. The Electric Field Generated by a Magnetic Dipole
By definition, at ϕ = 0 ([4], Eq.46.4)
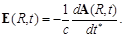 (91)
(91)
If to denote
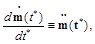 (92)
(92)
we obtain
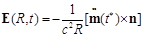 (93)
(93)
3.1.3. The Magnetic Field Generated by a Magnetic Dipole
By definition, at ϕ = 0 ([4], Eq.46.4)
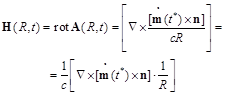 (94)
(94)
In general case, the rotor of the function F, depending on the parameter ξ, can be written as:
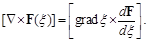 (95)
(95)
Therefore, since the grad t* = ∇(t – R /c) = – n /c, we obtain
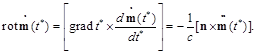 (96)
(96)
The differentiation of the second term of Eq. (94) gives
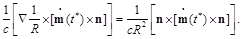 (97)
(97)
So the result is
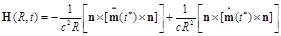 (98)
(98)
3.1.4. The Electromagnetic Field of a Harmonic Magnetic Dipole
Let the magnetic dipole varies harmonically
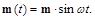 (99)
(99)
At this condition
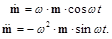
And
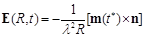 (100)
(100)
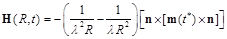 (101)
(101)
where λ = c /ω is the length of electromagnetic wave.
At large distances when R ≫ λ, the second term in brackets in the right-hand side Eq. (101) can be neglected.
Thus, the magnetic dipole in the case of harmonic oscillations creates in the wave zone an electromagnetic wave in which the amplitudes of the electric and magnetic fields are equal and orthogonal to each other.
3.1.5. The Scattering of Electromagnetic Waves by Electrons
Electromagnetic wave at falling on the charged particles causes their moving.
This movement of charges causes reemitted waves and eventually absorbtion of the incident wave. Electrons are the most efficient in this re-emission process.
Let an electromagnetic wave with amplitude of the electric field E and with intensity of radiation
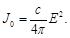 (102)
(102)
falls on a free electron.
Under the action of the incident wave, this electron acquires acceleration:
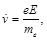 (103)
(103)
It will cause a wave of re-emission with the intensity [4]:
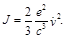 (104)
(104)
The ratio of the intensities of the reradiated wave and the incident one determines the cross section of this reaction:
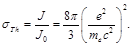 (105)
(105)
This mechanism is called the Thomson-scattering. The substitution of constants in the Eq. (105) indicates that the Thomson-scattering of photon by electron has value of about 1 barn.
3.2. The Magnetic Wave
3.2.1. The Heaviside Function and Its Derivatives
The Heaviside function is step function which is equal to 0 for negative argument and to 1 for positive one. This function requires an additional definition at zero-point. It is generally accepted to consider it equals to 1/2 at zero:
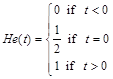 (106)
(106)
The first derivative from the Heaviside function 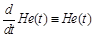 is the Dirac δ-function:
is the Dirac δ-function:
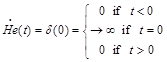 (107)
(107)
It is not simple to find the second derivative from the Heaviside function, since the delta-function is non-differentiable.
The Heaviside function can be represented approximately as the analytical expression:
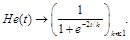 (108)
(108)
The coefficient k determines the sharpness of the step in zero-point.
Using the representation Eq. (108), we find that the second derivative from
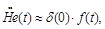 (109)
(109)
where
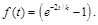 (110)
(110)
At taking into account the property of δ-function:
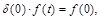 (111)
(111)
we obtain
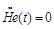 (112)
(112)
3.2.2. The Electromagnetic Fields of a Magnetic Dipole with Hopping
Time-Dependency
Let’s consider the field, which occurs if the time dependence of the magnetic dipole is described by Heaviside function m(t) = m He(t).
Due to the character of the behavior of the derivatives of this function, we can write
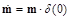 (113)
(113)
and
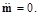 (114)
(114)
At using of Eqs. (93) and (108) we can conclude that the abrupt appearance of a magnetic dipole should not give a rising of electric field
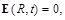 (115)
(115)
and the magnetic field far from the dipole appears as a delta-shaped splash
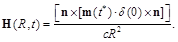 (116)
(116)
At a hopping occurrence of the magnetic dipole, a single δ-shaped splash of magnetic field arises.
This single δ-shaped splash or magnetic soliton reaches the observation point R at time t = R/c (where c is the velocity of soliton propagating), the spread of which is not accompanied by changes in the electric field. (A single δ-shaped splash of magnetic field seems conveniently to call as magnetic soliton.
A certain similarity of these objects exists, although usually solitons called heterogeneous solutions of nonlinear equations. In our case the single δ-shaped splash of magnetic field arises as the solution of linear Maxwell equations.)
3.2.3. β-decay and K-capture
In reality, the instant appearance of a magnetic dipole moment occurs during the β-decay. In accordance with the electromagnetic model of the neutron [1], the spin of relativistic electron equals to zero, when it together with proton forms neutron. The magnetic moment of electron in this its state do not observe. At β-decay of neutron, the relativistic electron acquires freedom, and together with it, spin and magnetic moment. As the emitted relativistic electron has velocity close to the speed of light, this process must have a saltatory character.
Experiments show that the β-decay of neutron is accompanied by the emission of antineutrinos:
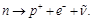 (117)
(117)
Thus, the δ-shaped splash of magnetic field that generated by hopping occur-rence of magnetic moment can be identified with antineutrino. The main prop-erties of these particles are the same: they have no charge, no rest mass, and very weakly interact with matter. Spin of electron in initial bounded state equals to zero [1]. After decay in final free state, its spin is ħ / 2. Given the law of conservation of angular momentum, magnetic soliton, just as neutrinos, should carry away the angular momentum equals to – ħ / 2.
The K-capture process should be another implementation of magnetic δ-soliton. In this process originally, electron forms an atom shell and has its own magnetic moment and spin. At some moment, it is captured by proton of nucleus and forms neutron together with it. This process can be described by an inverse Heaviside function, different from that was considered before (Eq. 106):
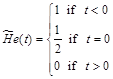 (118)
(118)
The inverse Heaviside function is equal to 1 at negative times and resets at t = 0.
A magnetic δ-soliton with the reverse direction of magnetic field to respect of its propagation vector R should occur during this process. Such "reverse" δ-soliton corresponds to neutrino in the K-capture reaction:
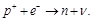 (119)
(119)
3.2.4. The Basic Physical Properties of Magnetic Soliton
The electromagnetic photon has equal largest electric and magnetic components and its spin equal to 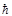 . Therefore, it should be assumed that the spin of magnetic photon which have magnetic component only must be equal to
. Therefore, it should be assumed that the spin of magnetic photon which have magnetic component only must be equal to 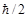 .
.
The decay of neutrons gives β-electrons with the energy spectrum from 0 to 782 keV. Accordingly, the maximum energy that can carry soliton in this decay is
 . (120)
. (120)
Let us evaluate other basic physical properties of magnetic soliton.
Its characteristic time
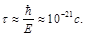 (121)
(121)
Its spatial extent
 . (122)
. (122)
The intensity of its magnetic field is very high
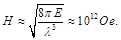 (123)
(123)
In order to assess the penetrating ability of magnetic soliton, we shall tray to estimate the cross section of its scattering by free electron.
The energy of interaction of the soliton with electron can be written as:
E = μ B H. (124)
Where μ B = eħ / 2me c is magnetic moment of electron.
One can assume that the electron energy after the acquisition of energy from soliton can be dissipated due to synchrotron radiation at the cyclotron effect.
Therefore electron reradiation at analogy with Eq. (104) will have intensity:
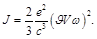 (125)
(125)
Where V is the free electron velocity in a scattering material, ω = μ B H / ħ is the electron cyclotron velocity in soliton magnetic field, the coefficient ϑ ≈ τω takes into account the fact that the time of action of the soliton magnetic field on electron is much smaller than the cyclotron period.
The intensity of the incident radiation can be written by analogy with Eq. (102) in the form
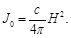 (126)
(126)
At assuming that the electron involved in thermal motion, we get v ≈ 3·106 cm/s.
As the result of simple calculations, we can estimate the ratio of the scattering cross section of magnetic soliton σ m on free electron to the cross section of the Thomson scattering calculated above σTh Eq. (105):
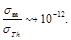 (127)
(127)
Those the capture cross section (scattering) of magnetic soliton in the substance can be roughly estimated as
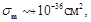 (128)
(128)
though of course this estimate is overstated because the re-scattering effect of synchrotron radiation in the case of a path of open cyclotron orbit should be considerably weaker.
3.2.5. Muon and Electron Neutrinos
The difference between the muon-neutrinos and electron-neutrinos was found by L. Lederman and his colleagues [15]. In this experiment, protons with energy of 15 GeV interacted with a target and produced a beam of high energy π± - mesons.
They in turn decayed and created high energy µ ± -mesons and neutrino νμ.
As a result, experimenters found that ν µ neutrinos cause reactions
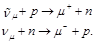 (129)
(129)
At that, reactions
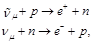 (130)
(130)
were not detected.
Authors of this measurement suggested that if between the muon- and electron-neutrinos would not be a difference, the electrons and positrons in these reactions would have to be produced as well as mesons in the reaction Eq. (129).
This assumption may be wrong. As reactions have different thresholds, their probability must be different.
Let us consider for example, the reaction of the birth of particle-antiparticle pairs.
Let the energy of γ-quantum is so great that the reaction of birth of pair proton-anitiproton is possible:
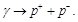 (131)
(131)
The same γ-quantum can lead to the birth of electron-positron pair:
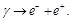 (132)
(132)
However, this does not happen.
This reaction is not energetically favorable. The reaction is energetically favorable if its products have the lowest kinetic energy and correspondingly take smaller volume in phase space.
If these reactions would be equiprobable, products of reaction Eq. (131) have been hammered by three orders large number of products of reaction (132).
This can also be attributed to reactions with neutrinos.
In order to carry out the reaction of Eq. (129), neutrinos must have energies above 100 MeV.
It is sufficient to overcome the threshold about 100 times smaller for the reaction of Eq. (130)
Therefore, the conclusion that ν µ and ν e are different particles can only be made at taking into account differences in these probabilities.
Assuming that these reactions come under the influence of high-energy mag-netic solitons, they both should be possible given their differences in probabili-ties. There should be no fundamental difference between them.
Moreover, if the neutrinos is magnetic solitons, it would be interesting to repeat the Lederman’s experiment at other conditions: to create a beam of muon-neutrinos with energies less than 100 MeV (ie below the threshold of birth of muons). In this case, we can expect the appearance only electrons and positrons in the yield of this reaction as it is prescribed by reaction Eq. (130).
Seeing neutrinos ν µ and ν e are magnetic solitons, they are characterized by different energies. Thence their mutual transformations seem impossible. It can be assumed that the problem of the solar neutrinos deficit should be solved not at a searching of their interference mechanism, but at a clarifying of definition of energetically favorable composition of the Sun core [16] and reactions inside it.
4. Mesons as Excited States of Electron
4.1. Excited States of Electron
The chain of reactions pion→muon→electron generates three neutrinos.
Charged pions (π ± -mesons), spin of which are zero, have not magnetic dipoles.
At the moment of conversion of π-meson into muon (µ-meson), the muon magnetic moment mμ = eħ / 2mμ c arises abruptly. It is accompanied by the emission of muon antineutrinos 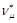 .
.
Further at the decay of muon, muon neutrino 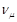 is radiated.
is radiated.
It is caused by the muon magnetic moment disappearance. At the same time the electron magnetic moment arises, which leads to the emission of the electron antineutrino 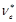 .
.
The fact that there are no other products except the neutrino and antineutrino in these reactions, leads us to the assumption that pion and muon should be excited states of electron.
These mesons have masses
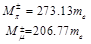 (133)
(133)
Let us assume that the excited state of the electron is formed due to the fact that a point particle with mass
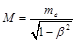 (where β = v /c) and charge e rotates in a circle of radius R with a speed v → c.
(where β = v /c) and charge e rotates in a circle of radius R with a speed v → c.
We will assume that stable excited states will be those for which the de Broglie wavelength is placed on the circumference of an integer times:
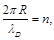 (134)
(134)
where λD = 2πħ / P is the de Broglie wavelength,
P is generalized momentum of the particle, n = 1,2,3... is integer.
At that the invariant kinetic angular momentum (spin) of particle
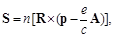 (135)
(135)
where p = me c is mechanical momentum of particle,
A = [m × R] /(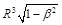 is the vector potential of the magnetic field generated by the rotating charge (see Eq (17)).
is the vector potential of the magnetic field generated by the rotating charge (see Eq (17)).
Considering the magnetic moment of gyrating charge e
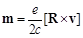 (136)
(136)
we obtain
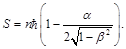 (137)
(137)
Where α = e2 / ħc is fine structure constant.
4.2. Excited State with n = 1 and S = 0
According to Eq. (137) the condition S = 0 corresponds to such a particle velocity at which the coefficient 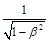 is equal to 2/α. The mass of the particle, because of its relativistic increasing, is equal to
is equal to 2/α. The mass of the particle, because of its relativistic increasing, is equal to
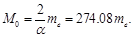 (138)
(138)
This value is very close to the mass of π ± -meson Eq. (133), which spin is zero:
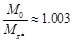 (139)
(139)
4.3. Excited State with n = 2 and S = ħ / 2
At n = 2 and S = ħ / 2, the coefficient 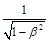 must be equal to 3/2α.
must be equal to 3/2α.
At that mass of the particle, because of its relativistic increasing, is equal to
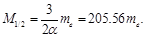 (140)
(140)
This value is very close to the mass of µ ± -meson (spin ħ / 2):
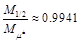 (141)
(141)
4.4. Excited State with n = 3 and S = ħ
At n = 3 and S = ħ, the coefficient 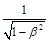 must be equal to 4/3α.
must be equal to 4/3α.
At that mass of the particle, because of its relativistic increasing, is equal to
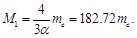 (142)
(142)
Mesons with these values of mass are not described in the literature.
5. Conclusion
In physics of the 20th century, some of these far-fetched theory became commonly accepted [17]. The reason for this is probably that not all method may confirm the value of a theory. Since the construction of a table representing the quark structure of elementary particles illustrates the ability to systematization but not proof of the correctness of the quark description. The main symptom of a quasi-theories is that they can not give an explanation of the individual primary characteristics of the objects and try to explain the general characteristics of the phenomenon as a whole. The fact that the electromagnetic model of the neutron allows us to predict all of its most important characteristics, forces us recognize that the neutron is not an elementary particle. The ability to calculate the pion mass, based on its spin, also says that the pion is not an independent elementary particle, and is, together with a muon, just excited electronic states. For this reason, an use of presentation of structure of elementary particles based on quarks with fractional charge appears to be erroneous.
The force of attraction between the protons arising at the relativistic electron exchange allow us to explain the mechanism of occurrence of nuclear forces (in the case of light nuclei). This gives possibility do not use gluons for it and to simplify this theory.
References
- Vasiliev B.V. About Nature of Nuclear Forces, Journal of Modern Physics, v.6, N5, 648-659 (2015).http://www.scirp.org/Journal/PaperInformation.aspx?PaperID=55921.
- Beringer J. et al.: Phys.Rev., D86, 010001, 2012.
- Bethe H.A. and Morrison P. Elementary Nuclear Theory. NY, 1956.
- Landau L.D. and Lifshitz E.M. The Classical Theory of Fields (vol. 2 of A Course of Theoretical Physics). Pergamon Press, N.Y., 1971.
- G.Joos, I.M. Freeman: Theoretical Physics (Volume 2)., Dover Publications, (1958).
- Zeldovich Ja.B. UFN, N6, 1965.
- Ioffe B.L. and Smilga A.V. Nuclear Physics B232 109...142, 1984.
- Vasiliev B.V. Is neutron an elementary particle? Prepint JINR, Р3-2014-77, Dubna, 2014. (In Russian).
- Heitler W., London F. Wechselwirkung neutraler Atome und homöopolare Bindung nach der Quantenmechanik. ZeitschriftfurPhysik, 44,pp. 455...472, 1927.
- Flugge S.: Practical Quantim Mechanics I, Berlin-NY, (1973).
- Glasston S.: Theoretical Chemistry, NY (1948).
- Motz H.T., Carter R.E. and Fisher P.C. Bull.Am.Phys.Soc., 4, No. 8, 477, D8, 1959.
- Monaham J.E., Raboy S. and Trail C.C. Nucl.Phys., 24, 400, 1961.
- Tamm I.E. Neutron-Proton Interaction. Nature 134, 1011, 1934.
- Danby G., Gaillard J-M., Goulianos K., Lederman L.M., Mistry N., Schwartz M., and Steinberger J. Phys. Rev. Lett. 9, 36, 1962.
- Vasiliev B. Physics of Star and Measurement Data, part I. Universal Journal of Physics and Application, 2 (5), 2014. – pp. 257...262.
- Vasiliev B. On the Disservice of Theoretical Physics (Work on the Bugs), Journal of Pure and Applied Physics, Volume 3, Issue 2, http://www.rroij.com/open-access/on-the-disservice-of-theoretical-physics-work-on-the-bugs.php?aid=61047