Study of the Carson Integral from 1926 to Present Time

T. Lazimov¹, E. Saafan²

¹Electric Supply and Insulation Department, Technical University of Azerbaijan, Baku, Azerbaijan

²Electrical Engineering Department, University of El-Mansoura, Mansoura, Egypt

Email address

Citation

T. Lazimov, E. Saafan. Study of the Carson Integral from 1926 to Present Time. International Journal of Electrical and Electronic Science. Vol. 3, No. 3, 2016, pp. 13-18.

Abstract

90 years ago John R. Carson had published his well-known article devoted to the study of earth influence on propagation of electromagnetic waves along long lines. The Carson integral determines earth’s contribution to the some parameters of double-wired aerial system, such as intensity of electrical field and mutual impedance and also to the magnetic vector potential of a single aerial wire. It have had great importance for the areas of computation and modeling of switching and atmospheric overvoltages in high-voltage electric power systems, electromagnetic compatibility, high-frequency relay protection and communication in electric power systems and other ones concerned to propagation of electromagnetic waves along long lines. The history of the problem and integral formulated by Carson and its development during the last ninety years is considered in the present paper.

Keywords

Carson Integral, Ground Return Impedance, Skin-Effect, Multi-layered Ground, Neumann and Hankel Functions, Struve and Lommel Functions

1. Introduction

Intensive development of electric power transmission lines and systems and wire communication taken place in the first quarter of the previous century had required formation a comprehensive theory of electromagnetic waves propagation along long electrical lines. Obviously the adequacy of this theory depended on consideration of the most influencing factors in the formulae and conditions included in the mathematical models.

One of the most influencing phenomena in this connection is interaction of electromagnetic waves, propagating along electrical lines with earth having impact to the some parameters of double-wired aerial line, such as intensity of electrical field and mutual impedance (determined via so called ground return parameters) and also to the magnetic vector potential of a single aerial wire.

The problem of determination ground return parameters had been firstly given and solved by John R. Carson in [1]. The ground return parameters were studied here for the case of homogeneous quasi-conductive half-cylindrical infinity earth. Carson considered the system of two parallel wires with ground return which is a basic one because that solution obtained may be extended for the multi-wired systems [2]. Assumptions done in [1] especially neglecting of displacement currents in earth and air led to notable dependence of solutions adequacy on frequency. Thus neglecting of displacement currents in air restricted the adequacy band within quasi-stationary frequencies, in earth – within frequencies corresponded to quasi-conductive earth.

The Carson integral is expressed as the following:

                                         (1)

In the given formula Z is modified linear impedance, Ohm/m; R is ground return resistance, Ohm/m; j is imaginary unit; ω is angular frequency, rad/s determined as ω=2πf; L is ground return inductance, H/m; µ is magnetic permeability, H/m; γ is ground’s specific conductivity, S/m; h_m and h_n are the mean highs of the two-wired system conductors with indexes m and n; a is the projection of distance between these conductors to the horizontal plane [1].

The geometrical parameters in the Carson problem are presented below in the Fig. 1. The distances D_mn and d_mn determine double-wired aerial line’s mutual inductance with no taking into account earth contribution (see [1]), m^/ and n^/ are the mirror reflections of the wires m and n respectively.

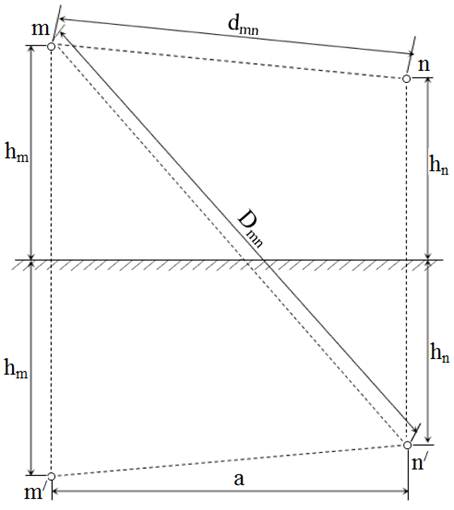
Fig. 1. Geometrical parameters in the Carson problem.

2. Initial Period Approximate Solutions

Carson had obtained the solution of the integral (1) due to indirect integration. The solution is expressed via anonymous series formulae for small values of argument, and asymptotic formulae for large values of argument. The worst exactness of the solution takes place at intermediate values of arguments.

If characterize in general the solution obtained by Carson it may be noticed that its adequacy depends on frequency, at this the less exactness takes place at intermediate arguments [1]. The solution given in [1] cannot be physically interpreted.

It must be noted that in the same time with J. Carson the problem had been studied by F. Pollaczek [3]. So some researchers call the problem and its solutions both by names of Carson and Pollaczek.

The Carson integral and solution presented in [1] have had the great importance in several areas including electromagnetic waves’ propagation along long lines, computation and modeling of switching and atmospheric overvoltages in high-voltage electric power systems, electromagnetic compatibility etc.

Remind that just the formulae for the impedance of double-wired electric line passing above superconductive infinity earth (so called Lecher’s line) were known before the above-minded articles of Carson and Pollaczek. In this formulation of the problem earth gives no contribution in the line parameters i.e. for this case there are zero ground return parameters [4].

The integral formula given by Carson for conductive homogeneous earth was extended for the case of earth having dielectric properties via presence dielectric permittivity of ground in the integrand by W. H. Wise [5]. The corresponding Wise modification of the Carson integral is as follows:

              (2)

where ε₀=10^-9/(36π), F/m is the dielectric constant.

Unlike the first expression offered by Carson in [1] its Wise modification and corresponding solution allow take into consideration longitudinal displacement currents in earth and determines ground return parameters in quasi-stationary frequency band. Alike the Carson solution the Wise one is less exact in intermediate argument’s band and cannot be physically interpreted because of anonymity of series and asymptotic formulae included in the solutions.

Add that during a few years after 1926 there were published some other notable papers e.g. [6,7]. In particular, in [6] Carson showed that the ground return impedance is substantially independent of the depth of the wire below the surface.

One of the general features of the above-minded solutions is that they are approximate ones. The further developing of the problem is discussed below.

3. Further Developing and Analytical Expressions

There were published dozens of articles and papers concerned to the problem under consideration in the second half of the previous century.

In [8] was given a comprehensive theoretical background of the Carson problem.

In [9] ideas of Carson and Pollaczek had been extended to cases of three-phase power transmission lines.

In [10] the approximate formulae for determination a module and phase of complex mutual impedance between single-wired lines taking into consideration finite conductivity of ground were obtained. The cases of lines crossing and their parallel and oblique approach were considered. The standard method of separation of real and imaginary components of integrand used in the work led just to increasing of independent variable power and did not allow obtain an exact analytical solution of the Carson integral.

In [11] L. Perelman presented a new analytical expression of Carson integral for homogeneous ground got by direct integration. The Perelman solution is as follows:

             (3)

Where K_mn is some function of geometrical parameters of aerial line, physical parameters of earth and frequency that determined as,

                               (4)

The necessary condition of adequacy of these formulae is Re(ϑ) > 0.

The second item of the above-presented solution contains the first-order Neumann function N₁ and given by,

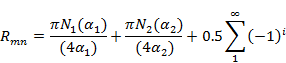
                        (5)

The third one – the zero-order Hankel function of the first kind  that expressed as,

                   (6)

here σ, m₀ and k are some wave propagation factors (see [11]).

In this view we would like to notice the following features of the Perelman solution:

Ÿ unlike the Carson solution it (the sum of the first and second items) is exact in the intermediate argument’s band;

Ÿ it is more exact in the quasi-stationary frequencies band in comparison with the Wise solution. Note in this view that appearance in the solution the Hankel function is conditioned by taking into consideration longitudinal displacement currents;

Ÿ unlike the anonymous series and asymptotic formulae in the solutions got by Carson and Wise it includes some known specific functions (the Neumann function N₁ and the Hankel function ). This eases estimation of exactness of approximate solutions and gives presuppositions for physical interpretation of solutions. Note in this connection that the Hankel functions are the only ones approached to zero at approaching complex arguments to infinity [12].

For easement of calculation by the formulae given in [11] there had been worked-up the tables presented in [13].

In [14] was presented a solution of the Wise modification for the case of the earth assumed to consist of a homogeneous stratum of a specified depth of one resistivity above a second homogeneous semi-infinite earth of different resistivity, i.e. there had been considered and solved the problem for two-layered earth in which layers is differed just by resistivity. As much as we know this was the first (or at least one of the first) researches of the problem under consideration for non-homogeneous ground.

In [15] was presented a solution for vector potentials in the problem considered given in formulation of [14] for a very general case free of the previous simplifying assumptions. Generality of the solution presented in [15] is ensured by specifying the vector potential as the sum of complementary magnetic and electric-wave components, in each of the two regions. The solution obtained is also extended to the multi-conductor case (e.g. three-phase aerial power transmission line). Note that the solution considered is concerned just to vector potential.

Another work dedicated to studying vector potentials in the Carson problem is [16]. A solution presented here by V. Bursian contains the difference of the first-order Struve and Neumann functions that let us give deeper physical interpretation of the solution.

Later it was obtained and presented in [17] a new analytical expression for ground return parameters at intermediate arguments which also included the first-order Struve and Neumann functions and its approximations for high and low frequencies. In [18] was got the following formula expressing ground’s impedance Z as a sum of the first-order Struve and Lommel functions.

                                         (7)

Where Z = (1+j)(ωμ/2γ)^1/2 is the homogeneous earth wave impedance; K_g1 and K_g2 are the coefficients depended on aerial line’s geometrical parameters; x₁ and x₂ are arguments of the Struve and Lommel functions depended on line’s geometry and depth of penetration of electromagnetic wave in ground [17]; H₁ is the first order Struve function; S₁ is some first-order Lommel function (see [18]).

There was given the physical interpretation of these functions, the Struve function as one presenting the component of solution related with static potential of electrical charges and the Lommel function as one related with changed magnetic field of current [17, 18].

In [19] the solution got in [17] had been extended to quasi-stationary frequencies band, the appropriated high and low-frequency approximations were got. There also was evaluated the maximum border frequency at which electromagnetic waves propagated along aerial lines may be considered as flat ones.

There would be right to remind some other notable works concerned to the considered problem especially [20, 21, 22] where the computational features of the problem were studied and also [23, 24] in which some physical phenomena and features related were analyzed.

4. Ground Return Parameters for the Case of Non-homogeneous Earth

As it is seen from the above given analyze the solutions of the Carson integral for electrically homogeneous ground have been obtained either as approximate and exact ones. It means that this integral does exist in the terms of general value.

As much as we now there have been published just a few works on existence of Carson integral’s solution for the case of non-homogeneous earth.

In particular, in [25] was got a principal value of Carson integral for non-homogeneous earth. As it had been shown later the integral under consideration does not exist in the terms of general value [26].

Let us now consider the known approximate solutions for the case of heterogeneous (multi-layered) ground.

Computation of Carson integral for multi-layered earth requires implementation of calculations using digital methods by the following formula (e.g. see [25]):

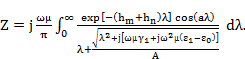                   (8)

Where A is a function containing the information on layers’ parameters such as their depth, conductivity, dielectric permittivity and magnetic permeability. E.g. for the case of three-layered earth it is expressed as follows:

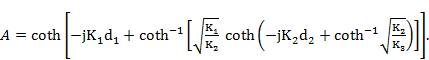                                     (9)

Where d₁ and d₂ are the depths of the upper and second layers of multi-layered ground, wave factors k₁, k₂ and k₃ are determined correspondingly as follows:

                    (10)

Computation of return parameters through the multi-layered ground is not trivial problem and it has some features. Fortunately for the high frequencies there is possible to make it solving easier.

Due to the skin-effect in earth for high frequencies of electromagnetic waves propagated along electrical lines there has taken place very little differences between ground return parameters calculated for homogeneous and heterogeneous (multi-layered) earth respectively. For high frequencies it was offered to consider heterogeneous earth as a homogeneous one having electrical parameters of the multi-layered earth’s upper layer [27].

This offering was developed later in [28, 29]. In particular, in [28] some features of calculation ground return impedance of double-wired aerial line passing above the multi-layered ground are considered in the article. The conditions at which the three-layered ground can be presented as homogeneous medium having parameters of the ground’s upper layer were determined for the two typical structures of multi-layered ground, in [29] the corresponding errors of such a presentation and their frequency dependences were evaluated for some earth’s structures and parameters.

In the Fig. 2 are presented relative differences of Z(f) values for multi-layered and homogeneous earth at different depths of layers of multi-layered earth calculated for the case of the structure "fresh water – granite – basalt" [28].

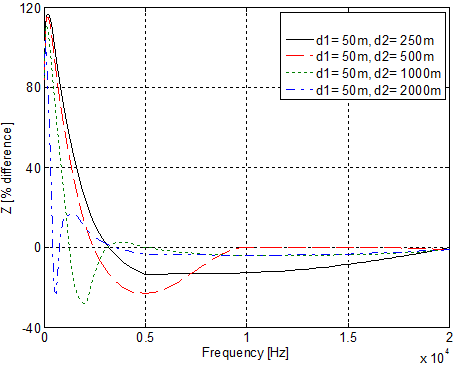
Fig. 2. Relative differences of ground return impedances against frequency for the structure "fresh water– granite – basalt".

As it is seen from this figure there takes place consistent decreasing of relative difference at increasing of frequency that means consistent convergence the Z(f) characteristics for multi-layered (three-layered in the considered case) and homogeneous ground conditioned by skin-effect.

There is necessary to remind the notable contribution has been made to the problem considered by A. Ametani and his co-authors. Their researches cover a wide area including determination of induced voltages in some transitional regimes (e.g. see [30, 31]), fundamentals of wave propagation theory (e.g. see [32, 33]) etc.

There have been other researchers but above reminded ones who have studied the problem under consideration. The authors of the present paper are apologizing for the impossibility to remind all the researchers have contributed in the theory and applications of the Carson integral.

5. Conclusion

The Carson integral, formulated ninety years ago, has had great importance for the problems associated with electromagnetic waves propagation along long lines (research of transitional processes and electromagnetic compatibility in electric power systems and designing high-frequency relay protection and communication, electric prospecting), taking into consideration influence of earth. There were solved several problems and obtained numerous solutions for the intensity of electromagnetic field, ground return parameters and magnetic vector potential at different frequency bands corresponded to the small, intermediate and high arguments, earth structure (homogeneous and multi-layered), investigated existence of the Carson integral for multi-layered earth in the terms of general and principal values and other results during these years.

References

1. J. R. Carson, "Wave propagation in overhead wires with ground return," The Bell System Technical Journal, Vol. 5, No. 4, pp. 539-554, Oct. 1926.
2. L. M. Wedepohl, "Wave propagation in nonhomogeneous multi-conductor systems using the concept of natural modes," Proceedings of the Institution of Electrical Engineers, Vol. 113, No. 4, pp. 622-626, Apr. 1966.
3. F. Pollaczek, "Uber das feld einer unendlich langen wechselstrom durchlossenen einfachleitung," E. N. T., Vol. 3, No. 9, pp. 339-359, 1926.
4. Arnold Sommerfeld, "Electrodynamics – Lectures on Theoretical Physics," Volume III, Academic Press, 1964.
5. W. H. Wise, "Effect of Ground Permeability on Ground Return Circuits," The Bell System Technical Journal, Vol. 19, No. 10, pp. 472-484, 1931.
6. J. R. Carson, "Ground return impedance: Underground wire with earth return," The Bell System Technical Journal,Vol. 8, No. 1, pp.94–98, Jan. 1929.
7. W. H. Wise, "Propagation of free frequency currents in ground return systems," Proceeding of the IRE, Vol. 22, No. 4, pp. 522-527, 1934.
8. G. A. Grinberg, B. E. Bonstedt, "Fundamentals of the exact theory of transmission lines’ wave field," Technical Physics, Vol. 24, No. 1, pp. 62-69, 1954 (in Russian).
9. M. V. Kostenko, "Propagation of sinusoidal waves along three-phase line with parallel wires," Electricity, No. 8, pp. 1-8, 1959 (in Russian).
10. M. V. Kostenko, "Mutual impedances between overhead lines taking into account skin-effect," Electricity, No. 10, pp. 29-34, 1955 (in Russian).
11. L. S. Perelman, "Refinement of wave propagation theory in the view of some technological problems," NIIPT Transactions, Vol. 10, pp. 103-120, 1963 (in Russian).
12. Milton Abramowitz, Irene Stegun, "Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables," NY, USA, Dover Publications, 1964.
13. L. S. Perelman, "Tables of the Carson integral for calculation wave propagation," NIIPT Transactions, Vol. 11, pp. 342-360, 1965 (in Russian).
14. L. M. Wedepohl, R. G. Wasley, "Wave Propagation in Multi-conductor Overhead Lines - Calculation of Series Impedance for Multilayer Earth," Proceeding IEE, Vol. 113, No. 4, pp. 627-632, Apr. 1966.
15. L. M. Wedepohl, A. E. Efthymiadis, "Wave Propagation in Transmission Lines Over Lossy Ground - A New Complete Field Solution", Proceeding IEE, Vol. 125, No. 6, pp. 505-510, Jun. 1978.
16. V. R. Bursian, "Theory of electromagnetic fields used in electrical exploration," Leningrad: Nedra, 1972 (in Russian).
17. T. M. Lazimov, "Analytical expression of Carson integral for electrically homogeneous ground," Electricity, No. 8, pp. 66-72, 1993 (in Russian).
18. T. M. Lazimov, "Research of magnetic influence of power electric networks on techno-sphere," Abstracts of DSc thesis, Baku, Azerbaijan, 1997 (in Russian).
19. T. M. Lazimov, "Analytical expression for the resistance of electrically homogeneous ground taking account its dielectric properties," Russian Electrical Engineering (New-York edition), Vol. 66, No. 2, pp. 27-31, 1996.
20. L. M. Wedepohl, C. S. Indulkar, "Wave Propagation in Non-Homogenous Systems: Properties of the Chain Matrix," Proceeding IEE, Vol. 121, No. 9, pp. 997-1000, Sep. 1974.
21. C. Gary, "Approche complete de la propagation multifilaire en haute frequency par utilization des matrices complexes," EDF Bulletin de la Direction des Etudes et Recherches, Serie B, No. 3-4, pp. 5-20, 1976.
22. T. Noda, "A double logarithmic approximation of Carson's ground return impedance," IEEE Transactions on Power Delivery, Vol. 21, No. 1, pp. 472-479, 2006.
23. C. Gary, A. Timotin, and D. Cristescu, "Prediction of surge propagation influenced by corona and skin effect, Physical Science, Measurement and Instrumentation, Management and Education - Reviews," IEE Proceedings, Vol. 130, No. 5, pp. 264-272, 1983.
24. Utkarsh R. Patel, Piero Triverio, "MoM-SO: a Complete Method for Computing the Impedance of Cable Systems Including Skin, Proximity, and Ground Return Effects," IEEE Transaction on Power Delivery, Vol. 30, No. 5, pp. 2110-2118, Oct. 2015.
25. V. I. Glushko, "Methods for calculation magnetic influence between electric circuits taking into consideration finite conductance of earth," Electricity, No. 3, pp. 6-18, 1986 (in Russian).
26. T. M. Lazimov, "On convergence of Carson integral for horizontally layered earth," Balkan Journal of Electrical & Computer Engineering," Vol. 1, No. 1, pp. 2-5, Apr. 2013.
27. T. M. Lazimov, "On computation of ground return impedance for multi-layered earth," Abstracts of the Seminar of the IV section of the USSR Academy of Sciences, Novosibirsk, 1983 (in Russian).
28. T. Lazimov, E. Saafan, "Some Features of Double-Wired Aerial Line’s Ground Return Impedance Calculation at Taking into Consideration Multi-Layered Earth’s Structure," AASCIT Physics, Vol. 1, No. 2, pp. 102-106, Apr. 2015.
29. T. Lazimov, E. Saafan, "Some Modeling Features of Horizontally-Layered Ground’s Return Parameters," Balkan Journal of Electrical & Computer Engineering, Vol. 3, No. 2, pp. 50-54, Sep. 2015.
30. T. Imamura,A. Ametani,"I nvestigation of transient induced voltage to a communication line from an overhead power transmission line," IEE Proceedings on Generation, Transmission and Distribution, Vol. 137, No. 2, pp. 129-138, 1990.
31. O. Goni, E. Kaneko,and A. Ametani, " Characteristics of the induced currents in horizontal conductors due to a nearby lightning strike," Proceedings of ICECE 2008, Dhaka, Bangladesh, pp. 32-37, Dec. 2008.
32. A. Ametani,R. Schinzinger,"Equations for surge impedance and propagation constant of transmission lines above stratified earth," IEEE Transactions on Power Apparatus and Systems,Vol. 95, No. 3, pp. 773-781, 1976.
33. A. Ametani,Y. Miyamoto,Y. Baba,N. Nagaoka,"Wave Propagation on an Overhead Multiconductor in a High-Frequency Region," IEEE Transactions on Electromagnetic Compatibility,Vol. 56, No. 6, pp. 1638-1648, 2014.

Biography