| 1. | ||
| 2. | ||
| 3. | ||
The Behavior of Cauchy-Type Integral Near the Boundary of the Semicylindrical Domain
A. Gaziev1, M. Yakhshiboev2
1Faculty of Mechanical-Mathematics of Samarkand State University, Samarkand, Uzbekistan
2Samarkand Branch of Tashkent University of Informational Technology, Samarkand, Uzbekistan
Email address
 (M. Yakhshiboev)
(M. Yakhshiboev) Citation
A. Gaziev, M. Yakhshiboev. The Behavior of Cauchy-Type Integral Near the Boundary of the Semicylindrical Domain. International Journal of Mathematical Analysis and Applications. Vol. 3, No. 1, 2016, pp. 1-16.
Abstract
The purpose of this work is the elucidation of the behavior of Cauchy-type integrals near the boundary semicylindrical domain to ![]() - characteristics celebrated jordanovic of closed curves (in the case when θ(δ)~δ, this class of curves is much wider class of piecewise-smooth class of curves for which the chord length relation to the pulling together arch are limited (K-curves), and also in it existence of cusps is allowed). The main characteristics for functions
- characteristics celebrated jordanovic of closed curves (in the case when θ(δ)~δ, this class of curves is much wider class of piecewise-smooth class of curves for which the chord length relation to the pulling together arch are limited (K-curves), and also in it existence of cusps is allowed). The main characteristics for functions ![]() - the mixed and private modules of continuity which was proven continuously extendibility of
- the mixed and private modules of continuity which was proven continuously extendibility of ![]() multiple Cauchy-type integral to the border of the semicylindrical domain and the limit values of the types of Sokhoskiy’s formulas.
multiple Cauchy-type integral to the border of the semicylindrical domain and the limit values of the types of Sokhoskiy’s formulas.
Keywords
Closed Jordan Rectifiable Curve (c.j.r.c.), Semicylindrical Domain, Cauchy-Type Integrals, Private and Mixed Continuity Modules, Characteristic Curve Core, Continuous Extendibility, Sokhoskiy’s Formulas
1. Introduction
Let ![]() be a closed Jordan rectifiable curve (c.j.r.c.) with length
be a closed Jordan rectifiable curve (c.j.r.c.) with length ![]() and diameter
and diameter ![]() in the complex planes of variables
in the complex planes of variables ![]() . A bounded domain
. A bounded domain ![]() with the bound
with the bound ![]() we call an internal, the padding of
we call an internal, the padding of ![]() we call an external and denote by
we call an external and denote by ![]() .
.
The contours ![]() defines in whole complex space of
defines in whole complex space of ![]() variables
variables ![]() various semicylindrical domains which are obtained by all possible combinations of characters in the topological multiplication
various semicylindrical domains which are obtained by all possible combinations of characters in the topological multiplication
![]() .
.
Among them: one is of the type of ![]() (
(![]() ), which we denote by
), which we denote by ![]()
![]() are domains of the type of
are domains of the type of ![]()
![]()
![]() (
(![]()
![]()
![]() ) which we denote by
) which we denote by![]() ; similarly,
; similarly, ![]() are domains of the type of
are domains of the type of
![]()
![]()
![]()
(![]()
![]()
![]() )
)
which we denote by ![]() ) and etc..
) and etc..
Borders of all these semicylindrical domains have the common part, namely, ![]() which is called the core.
which is called the core.
If the function ![]() is defined in
is defined in ![]() and for an arbitrary
and for an arbitrary ![]() there exists
there exists
![]()
we say ![]() is continuously extended up to the bound of
is continuously extended up to the bound of ![]() . Analogically, define continuously extendibility up to core of domains
. Analogically, define continuously extendibility up to core of domains ![]() etc.. The corresponding limit values of the function
etc.. The corresponding limit values of the function ![]() is denoted by
is denoted by ![]() etc., respectively.
etc., respectively.
If ![]() is continuously extended up to core from the domain
is continuously extended up to core from the domain ![]() then we say that the function
then we say that the function ![]() is continuously extendible up to core. We say that a function
is continuously extendible up to core. We say that a function ![]() is continuously extended to the given boundary point of semicylindrical domain, if the function
is continuously extended to the given boundary point of semicylindrical domain, if the function ![]() tends to a given boundary point along any path, while remaining at all times in this semicylindrical domain. The corresponding limits we call boundary values
tends to a given boundary point along any path, while remaining at all times in this semicylindrical domain. The corresponding limits we call boundary values ![]() in this domain, and we denote them as well as the boundary values
in this domain, and we denote them as well as the boundary values ![]() on the core
on the core![]() , with the replacement
, with the replacement ![]() core of
core of ![]() corresponding boundary point. It is easily seen that if the function
corresponding boundary point. It is easily seen that if the function ![]() is continuously extended to the core
is continuously extended to the core ![]() from every
from every ![]() semicylindrical domain which boundaries have a common core of
semicylindrical domain which boundaries have a common core of ![]() , then it will continuously be extended to any boundary point of each of these semicylindrical domains.
, then it will continuously be extended to any boundary point of each of these semicylindrical domains.
Let us consider ![]() - multiple integral of Cauchy-type
- multiple integral of Cauchy-type
![]() (1)
(1)
where ![]() - is the space of continuous functions on
- is the space of continuous functions on ![]() .
.
In the paper [1] was studied the behavior of integral (1) for smooth contours and functions of Holder's class and in papers [2], [3] and [4] (for n=2) under some assumptions on the curves![]() and the function
and the function ![]() the continuity up to core of the integral was investigated. In [5] and [6] (for n=2) the investigation of the integral (1) was extended to a case of summable density. The papers [7], [8], [9] and [12] are focused on study the integral near a bicylindrical fields and [13-16] contain results the behavior of integral Martinelli-Bochner, which (1) turns into a Cauchy-type integral for n = 1.
the continuity up to core of the integral was investigated. In [5] and [6] (for n=2) the investigation of the integral (1) was extended to a case of summable density. The papers [7], [8], [9] and [12] are focused on study the integral near a bicylindrical fields and [13-16] contain results the behavior of integral Martinelli-Bochner, which (1) turns into a Cauchy-type integral for n = 1.
In the current work the behavior of ![]() -multiple integral (1) on the border of semicylindrical domain in terms of the continuity modulus and
-multiple integral (1) on the border of semicylindrical domain in terms of the continuity modulus and ![]() ) characteristic curve
) characteristic curve ![]() is studied under the most common assumptions concerning function
is studied under the most common assumptions concerning function ![]() and curves
and curves ![]() (it was first given in [7], and then generalized in [10], [15-17].) The paper is organized as follows: in the next section are presented some results and notations which will be used in the formulation of the main theorems. In Section 3 we give our main results and their proofs.
(it was first given in [7], and then generalized in [10], [15-17].) The paper is organized as follows: in the next section are presented some results and notations which will be used in the formulation of the main theorems. In Section 3 we give our main results and their proofs.
2. Preliminaries
For the brevity of the writing we introduce the following notations as in ![]()
![]()
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() .
.
![]() =(
=(![]() ),
),
![]() etc..
etc..
![]()
![]() etc..
etc..
![]() ,
,
![]() ,
,
![]() ,
,
![]() , etc..
, etc..
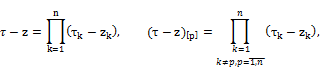
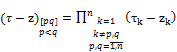 etc..
etc..
Then be these notations (1) takes form
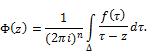
Let us denote by ![]() the following
the following
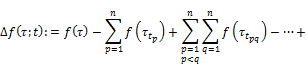
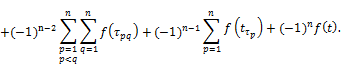
It is easy to verify that holds the identity

![]()
holds. Using this and (1) we have
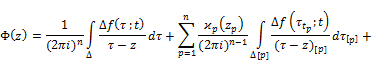
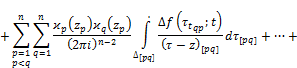
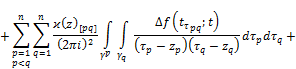
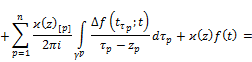
![]() (2)
(2)
where ![]()
The integrals on the right hand side in (2) we consequently denote by
![]()
which will be further used.
Let![]() be a closed rectiable Jordan curve (c.r.j.c.)
be a closed rectiable Jordan curve (c.r.j.c.)![]()
![]()
![]() be the length of the curve and
be the length of the curve and ![]() be an equation of the curve in arc coordinates
be an equation of the curve in arc coordinates ![]() . Let us denote
. Let us denote
![]()
![]()
The function ![]() is chosen as the main characteristics of the curve
is chosen as the main characteristics of the curve ![]() Monotonically increasing function
Monotonically increasing function ![]() defined by
defined by
![]()
is called a generalized inverse with respect to ![]() . The concept of generalized inverse function is introduced and studied in [8]. To investigate the behavior of integral (1) on the boundary of semicylindrical domain appears the following main characteristics to function
. The concept of generalized inverse function is introduced and studied in [8]. To investigate the behavior of integral (1) on the boundary of semicylindrical domain appears the following main characteristics to function ![]()
1). mixed continuity module (for the case ![]() was given in [11])
was given in [11])
![]()
where
![]()
2). private continuity modules

where
![]()

where
![]()
![]()
![]()
![]() ,
,
![]()
Let us denote by ![]() a multiple nonnegative monoton increasing function
a multiple nonnegative monoton increasing function ![]() on
on ![]() such that
such that ![]() and
and ![]() monoton decreases. By
monoton decreases. By
![]()
denote a set of functions ![]() defined on (
defined on (![]() and lying in
and lying in ![]() on each argument, i.e.,
on each argument, i.e., ![]() by
by ![]() at fixed
at fixed ![]() . It is clear that
. It is clear that
![]()
1). Let ![]() be a nonincreasing function on
be a nonincreasing function on ![]()
Then the following
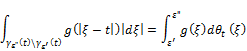
holds for arbitrary ![]()
2). Let ![]() be a nonincreasing function on
be a nonincreasing function on ![]() and
and ![]() satisfy the conditions
satisfy the conditions
![]() ,
, ![]() ,
, ![]()
then
![]()
3). Let ![]() be nonincreasing function on
be nonincreasing function on ![]() . Then
. Then
![]() .
.
Let us emphasize
![]()
![]() ….
….
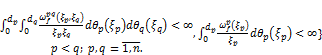 .
.
3. Main Results
Theorem 3.1. Let ![]() be a closed rectiable Jordan curve and
be a closed rectiable Jordan curve and ![]() Then for arbitrary
Then for arbitrary ![]() the following estimate holds
the following estimate holds
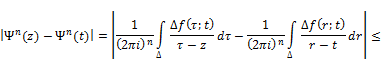
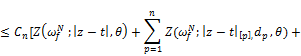
![]() (3)
(3)
![]() ,
,
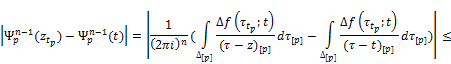
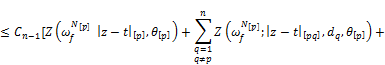
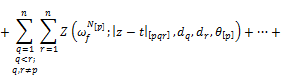

![]() (4)
(4)

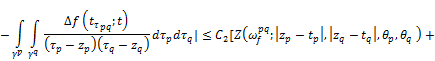
![]() (5)
(5)
![]()
![]() (6)
(6)
where
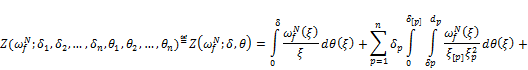

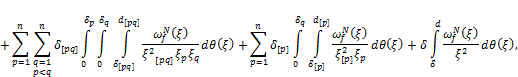
![]()
Proof. Let us denote by ![]() an arbitrary point of the border
an arbitrary point of the border ![]() Then the identity takes the place
Then the identity takes the place

![]() (7)
(7)
the validity of which is easily shown by direct calculations of items. It is easy to see also that
![]() (8)
(8)
Let us consider the difference
![]() (9)
(9)
Using (8) and (7) in (9) we obtain
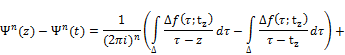

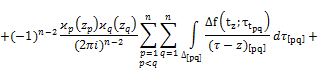

![]() (10)
(10)
Let us first denote items on the right hand side of equality in (10) by ![]() , respectively, and we estimate each of them separately.
, respectively, and we estimate each of them separately.
Before proceed to assess ![]() remind the is an identity
remind the is an identity
![]()
=![]()
![]() .
.
Let us consider
![]() (11)
(11)
The difference ![]() standing under the integral in
standing under the integral in ![]() , we replace with a right member of identity (11). Then we have
, we replace with a right member of identity (11). Then we have
![]()
![]()
![]() . (12)
. (12)
Let ![]()
![]()
The integral (12) is represent table a type of the sum of two integrals of ![]() and
and ![]() , taken, on
, taken, on ![]() and
and ![]() respectively, where
respectively, where
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Let us denote by
![]()
the integrals taken piecemeal cores![]() respectively. As for every
respectively. As for every
![]() (13)
(13)
we have
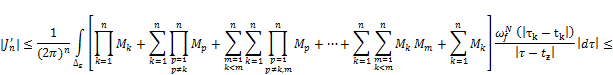

where

Consequently applying 1), 2), 3) of Lemma 2.1 and choosing ![]() we obtain
we obtain
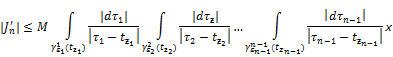

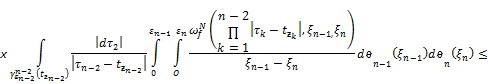
![]() .
.
Thus,
![]() (14)
(14)
Now we estimate ![]() For this aim we first estimate integral
For this aim we first estimate integral ![]() :
:
Now we estimate the integral ![]() as follows
as follows

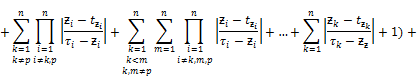
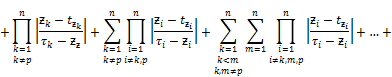
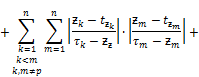
![]() .
.
From this and (13) we obtain the following
![]() 𝗑
𝗑
𝗑![]()
for every ![]()
![]() Taking into account that
Taking into account that ![]() and
and ![]() , from the last estimate we have
, from the last estimate we have
![]() 𝗑
𝗑
![]() . (15)
. (15)
Taking similar transforms which were used in the estimate of (15![]() we have for the integral
we have for the integral ![]() the following:
the following:
![]()
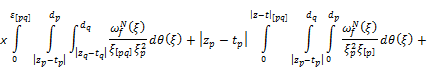
![]()
![]() (16)
(16)
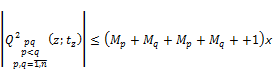

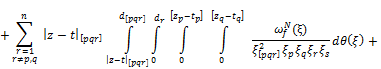
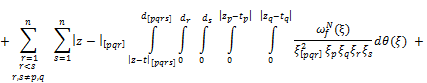
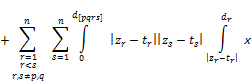
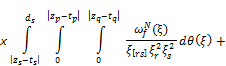

![]() (17)
(17)


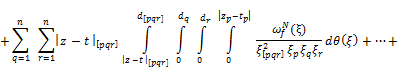
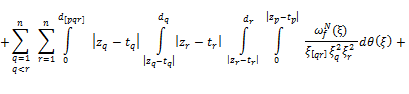

![]() , (18)
, (18)
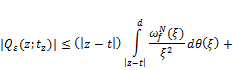
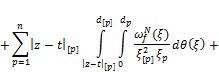
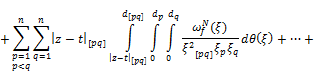

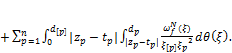 (19)
(19)
Summarizing the obtained estimates in (15![]() , we get an estimate for
, we get an estimate for ![]()
Now we estimate ![]() As
As ![]() applying items 1) and 2) of Lemma 2.1 we have
applying items 1) and 2) of Lemma 2.1 we have
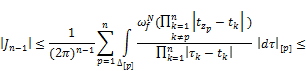
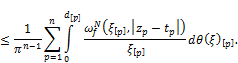
Owing to a lack of growth ![]()
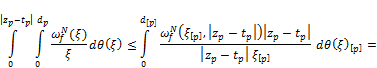
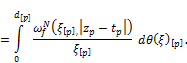
Therefore,
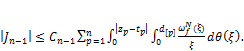 (20)
(20)
Similarly estimating the rest integrals we have
![]() (21)
(21)
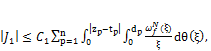 (22)
(22)
 (23)
(23)
For get an estimate for the integral ![]() we apply Theorem 2 in [18]. Summarizing all estimates for integrals
we apply Theorem 2 in [18]. Summarizing all estimates for integrals ![]()
![]() and
and ![]() and estimates (14), (
and estimates (14), (![]() and (
and (![]() -(23
-(23![]() we finally obtain the required estimate (
we finally obtain the required estimate (![]() .
.
To estimate the following difference
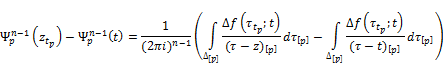
we use the following identity
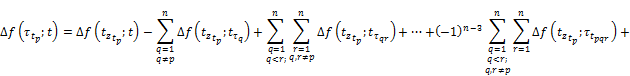
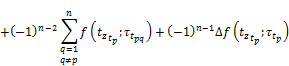
the validity of which follows from (7). Then ![]() is represented in a form of a difference (10) and is estimated also as estimates for
is represented in a form of a difference (10) and is estimated also as estimates for ![]() and
and ![]() the distinction consists only among integrals. Therefore, we obtain
the distinction consists only among integrals. Therefore, we obtain
![]()

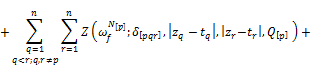

Similarly, we have
![]()
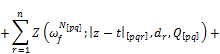
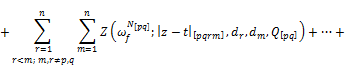

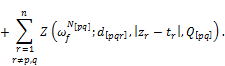
By continuing this process we show estimates for the differences
![]() ,
, ![]()
have the forms:
![]()
![]()
![]() .
.
These prove the theorem.
From the theorem immediately follow the following equalities
![]()
Theorem 3.2. If ![]() then for every
then for every ![]() the following estimate
the following estimate
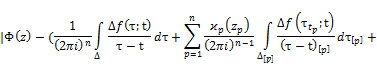

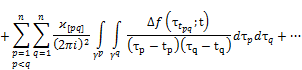
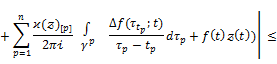
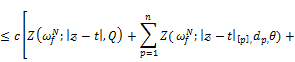
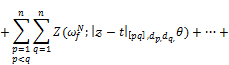


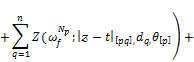
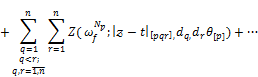


![]()
![]()
holds.
The proof follows from Theorem 3.1.
Theorem 3.3. Let ![]() (k=
(k=![]() ) - c.j.r.c.,
) - c.j.r.c., ![]() Then function
Then function ![]() continuously extendable on a core Δ from each of
continuously extendable on a core Δ from each of ![]() semicylindrical domains for which the core is common.
semicylindrical domains for which the core is common.
By Theorems 3.1 and 3.2 and taking into account (2), we get that the function ![]() is continuously extended to the cores Δ and for the limiting values of the function
is continuously extended to the cores Δ and for the limiting values of the function ![]() equitable Sokhotskii’s formulas:
equitable Sokhotskii’s formulas:
![]()
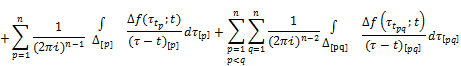
![]()
![]()
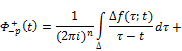
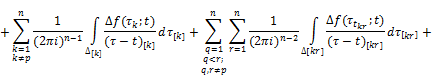

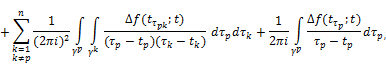
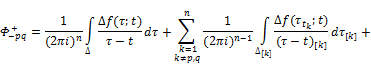

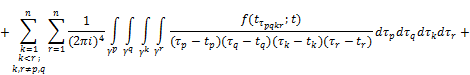
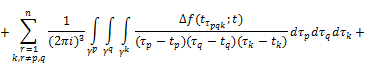
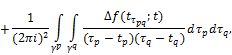
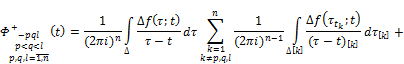
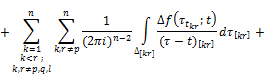
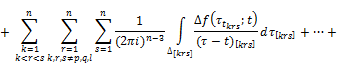
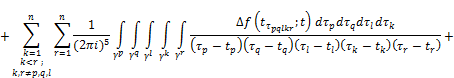
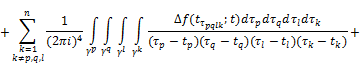
![]() ,
,
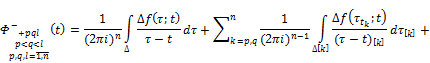
+![]()
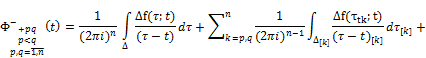
![]() , (24)
, (24)
![]() ,
,
![]() .
.
In particular, for the case ![]() , the Sokhotskii’s formulas (24) take the forms
, the Sokhotskii’s formulas (24) take the forms
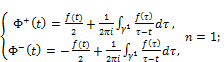 (25)
(25)
and for the case ![]()
![]()
![]() , (26)
, (26)
![]() (27)
(27)
![]() (28)
(28)
![]() (29)
(29)
Above we have shown the behavior of Cauchy-type integrals on the core ![]() of the border. Now we explain the behavior of the integrals on the whole boundary of the semicylindrical domain. To reduce the entries in detail, consider the case n=3 for
of the border. Now we explain the behavior of the integrals on the whole boundary of the semicylindrical domain. To reduce the entries in detail, consider the case n=3 for
![]() .
.
The boundary of this domain consists of the sets: ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;![]() ;
;![]() and
and ![]() .
.
The integral (1) for n=3 we write as follows
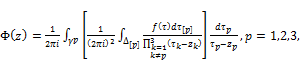 (30)
(30)
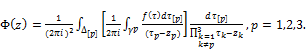 (31)
(31)
Let us consider integral (30) as integral of Cauchy-type of a complex variable with a core
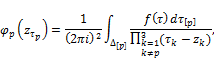
depending on the parameters ![]() and applying to them Sokhotskii's formulas (
and applying to them Sokhotskii's formulas (![]() of the variable
of the variable ![]() and we obtain
and we obtain
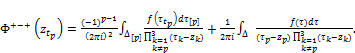 (32)
(32)
At p=1,2,3 the formula (32) gives boundary values of integral (1) in points of boundary sets: ![]() ;
; ![]() ;
; ![]() .
.
Considering integrals (31) as integral of Cauchy-type of two complex variables of ![]() with the core
with the core
![]() ,
,
depending on the parameter ![]() and applying to them Sokhotskii's formulas (
and applying to them Sokhotskii's formulas (![]() , (
, (![]() and (
and (![]() on the corresponding variables and obtain
on the corresponding variables and obtain
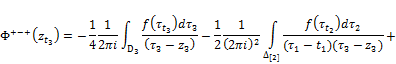
![]() (33)
(33)

![]() (34)
(34)
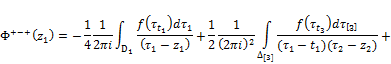
![]() (35)
(35)
Formulas (33), (34) and (35) give values of integral (1) at points of sets ![]() ;
; ![]() ;
; ![]() . All shifts integrals at a conclusion of formulas (32)-(35) are admissible as only shifts of special integrals with routine were applied. On a core Δ boundary values
. All shifts integrals at a conclusion of formulas (32)-(35) are admissible as only shifts of special integrals with routine were applied. On a core Δ boundary values ![]() are defined by Sokhotskii's formula (24).
are defined by Sokhotskii's formula (24).
Thus the following theorem is proven.
Theorem 3.4. Let ![]() r.j.c.c.,
r.j.c.c., ![]() Then the function
Then the function ![]() defined as (1) is continuously extended to the entire of border of the semicylindrical domain and the limiting values of the function Ф(z) are formulas such as Sokhotskii’s formulas for the case of the core (24).
defined as (1) is continuously extended to the entire of border of the semicylindrical domain and the limiting values of the function Ф(z) are formulas such as Sokhotskii’s formulas for the case of the core (24).
References