| 1. | ||
| 2. | ||
| 3. | ||
| 4. | ||
Disjoint Variation, (s)-Boundedness and Brooks-Jewett Theorems for Lattice Group-Valued k-Triangular Set Functions
A. Boccuto
Dipartimento di Matematica e Informatica, University of Perugia, Perugia, Italy
Email address
Citation
A. Boccuto. Disjoint Variation, (s)-Boundedness and Brooks-Jewett Theorems for Lattice Group-Valued k-Triangular Set Functions. International Journal of Mathematical Analysis and Applications. Vol. 3, No. 3, 2016, pp. 26-30.
Abstract
We consider some basic properties of the disjoint variation of lattice group-valued set functions and 
-boundedness for 
-triangular set functions, not necessarily finitely additive or monotone. Using the Maeda-Ogasawara-Vulikh representation theorem of lattice groups as subgroups of continuous functions, we prove a Brooks-Jewett-type theorem for -triangular lattice group-valued set functions, in which -boundedness is intended in the classical like sense, and not necessarily with respect to a single order sequence. To this aim, we deal with the disjoint variation of a lattice group-valued set function and study the basic properties of the set functions of bounded disjoint variation. Furthermore we show that our setting includes the finitely additive case.
Keywords
Lattice Group, Triangular Set Function, (Bounded) Disjoint Variation, Brooks-Jewett Theorem
1. Introduction
In the literature there have been several recent researches, about limit theorems for lattice-group or vector lattice-valued set functions. For a historical survey and related results see also [1-3] and their bibliographies. In this paper we deal with 
-triangular lattice group-valued set functions. Some examples of such set functions are the 
-measures, that is monotone set functions 
with 
, continuous from above and from below and compatible with respect to finite suprema and infima, which are 
-triangular set functions. The measuroids are examples of
-triangular set functions, not necessarily monotone (see also [4]).
In this paper, using the Maeda-Ogasawara-Vulikh representation theorem for lattice groups as subgroups of some suitable spaces of continuous functions, we extend to -triangular set functions some Brooks-Jewett-type theorems, proved in [5] in the finitely additive setting. Note that, in our context, 
-boundedness is intended in the classical like sense, and not necessarily with respect to a single order sequence. Observe that, differently than in the finitely additive setting, boundedness of k-triangular set functions, in general, does not imply -boundedness. Thus, we consider the disjoint variation of a lattice group-valued set function and prove that boundedness of the disjoint variation of is a sufficient condition (in general, not necessary) for -boundedness of .
2. Preliminaries
Let 
be a Dedekind complete lattice group, 
be an infinite set, 
be a 
-algebra of subsets of , 
be a bounded set function, and be a fixed positive integer.
A sequence 
in is called 
-sequence iff it is decreasing and 
. A sequence 
in is order convergent (or -convergent) to 
iff there exists an -sequence in such that for every 
there is a positive integer 
with 
for each 
, and in this case we write 
.
The positive and negative part of are defined by 
respectively.
The semivariation of is defined by
A set function is -bounded iff 
for every disjoint sequence 
in . The set functions 
, 
, are uniformly -bounded iff 
for any disjoint sequence in .
The set functions , , are equibounded iff there is 
with 
whenever and 
.
We say that is -triangular iff 
for any and 
for all 
, 
.
It is easy to prove the following
Proposition 2.1 If 
is -triangular, then also 
is -triangular.
3. The Main Results
We begin with observing that it is well-known that, if 
, are equibounded set functions, then the union of the ranges of the 
’s can be embedded in the space
, 
is continuous
(1)
where
is a suitable compact extremely disconnected Hausdorff topological space, existing thanks to the Maeda-Ogasawara-Vulikh representation theorem. Every lattice supremum and infimum in 
coincides with the respective pointwise supremum and infimum in the complement of a meager subset of (see also [6] and [7, p. 69]).
We will prove a Brooks-Jewett-type theorem for a sequence 
of lattice group-valued set functions. The technique we will use is to find a meager set 
such that the real-valued "components" 
, , are -bounded and pointwise convergent for any 
, and then to apply the corresponding classical results existing for real-valued k-triangular set functions (see also [2]). We require pointwise convergence of the ’s with respect to a single -sequence, in order to find a single corresponding meager set 
to obtain pointwise convergence of the "components" in 
. Concerning
-boundedness of the "components", observe that, differently from the finitely additive case, a bounded k-triangular set function, even monotone, in general is not -bounded, as we will see in (2). So, in our setting, we will give a condition which implies -boundedness of the "components". To this aim, we deal with the disjoint variation of a lattice group-valued set function (see also [2, 8-9]) and prove that boundedness of the disjoint variation implies -boundedness of the "components". Furthermore, we will show that our context includes the finitely additive case.
Now we give the following technical proposition.
Proposition 3.1. Let , be a sequence of equibounded set functions. If there is a meager set 
such that the set functions are real-valued and -triangular for every 
and , then the ’s are -triangular. Moreover, if the ’s are -triangular, then the set functions , , are real-valued and -triangular for every 
Proof: Thanks to (1), for every 
and the set function 
defined by 
, , is real-valued. Now we prove the first part. Let 
be as in the hypothesis, then
for every , with and 
, and
for all , and . Since is meager, by a density argument it follows that
for every , with , and 
for all and , that is is -triangular for every . The proof of the last part is straightforward.
Now we deal with -boundedness of -triangular set functions. In general, differently from the finitely additive setting, it is not true that every bounded -triangular capacity is -bounded. Indeed, let 
, set
(2)
if 
, 
. It is not difficult to see that is bounded, positive, monotone and -triangular. For each disjoint sequence 
of nonempty subsets of it is 
for every 
, and so it is not true that 
. So, is not -bounded. So, we consider the disjoint variation of a lattice group-valued set function.
Definitions 3.2. Let us add to an extra element 
, obeying to the usual rules, and for any set function let us define the disjoint variation 
of by
where the involved supremum is taken with respect to all finite disjoint families 
such that 
and 
for each 
.
A set function is of bounded disjoint variation (or 
) iff 
.
Examples 3.3. We give an example of a 1-triangular monotone set function, which is not . Let be as in (2). It is easy to check that 
. Pick arbitrarily and put 
, 
. It is 
, and so 
. From this and arbitrariness of 
we get 
, and hence is not . Thus, boundedness does not imply , though it is easy to see that the converse implication holds.
We give an example of a 1-triangular monotone set function, which is but not finitely additive. Let 
, 
,
, 
Note that 
is not increasing, since 
. It is easy to see that is -triangular. Hence, by Proposition 2.1, is -triangular.
Note that is positive and monotone, and
(3)
where the involved supremum is taken with respect to all finite disjoint families such that 
for every , and hence is . Note that the supremum in (3) is exactly equal to 
: indeed, it is enough to consider, for each , the family 
: 
and to take into account that 
for any . Finally, it is 
Thus, is not finitely additive.
We now show that, in general, -boundedness does not imply . Let 
, be the -algebra of all Borel subsets of , 
, , where sgn
if 
, sgn
if 
and sgn
, and set 
, . Note that is not monotone: indeed,
Now, fix arbitrarily and pick 
, 
, 
,
,
, 
, ,,. It is
and hence, by arbitrariness of , it follows that is not .
We now prove that is -triangular. Pick any two disjoint sets 
, 
. Then, it is
= 
= 
= 
= 
,
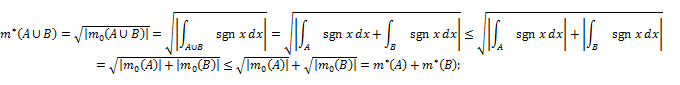
getting 1-triangularity of 
Set 
, . Note that is positive and increasing. Since is not , then a fortiori is not. By Proposition 2.1, is -triangular, since is. Moreover, it is not difficult to see that is -bounded. Hence, is -bounded (see also [9, Theorem 2.2]). Thus, property is not a necessary condition for -boundedness of -triangular set functions.
Now we prove that is a sufficient condition for -boundedness of a set function with values in a lattice group and of its real-valued "components".
Proposition 3.4. Let be a set function, and be as in (1). Then the set function 
is real-valued, and -bounded for every 
. Moreover is -bounded.
Proof. Since is bounded, arguing analogously as at the beginning of the proof of Proposition 3.1, for any the set function 
defined by 
, , is real-valued. For each
it is
since the pointwise supremum is less or equal than the corresponding lattice supremum in 
. So, is for each . By [8, Theorem 3.2], for each disjoint sequence 
in and it is 
, and a fortiori 
. This proves the first part.
Now, choose any disjoint sequence in . By the Maeda-Ogasawara-Vulikh representation theorem (see also [6]) there is a meager set with
for every . From this we obtain 
for each . By a density argument, we get for every , namely 
By arbitrariness of the chosen sequence , we have -boundedness of .
Now we show that our setting includes the finitely additive case. Indeed we have the following
Proposition 3.5. Every bounded finitely additive measure is .
Proof: First of all consider the case in which is positive. Then, thanks to finite additivity, is also increasing. If is any disjoint finite family of subsets of , whose union we denote by 
, then we get
(4)
(see also [2, Proposition 3.4]). From (4) and boundedness of we deduce that 
is , at least when is positive. In the general case,
, where 
and 
are the positive and the negative part of , respectively. Proceeding analogously as in [10, Theorem 2.2.1], it is possible to check that and are finitely additive. Then, by the previous case, and are , and
(5)
Taking in (5) the supremum with respect to 
, we get the assertion.
Now we are in position to prove the following Brooks-Jewett-type theorem, which extends [5, Theorem 3.1] to the context of -triangular set functions.
Theorem 3.6. Let 
be as in (1), 
, , be a sequence of BDV -triangular equibounded set functions. Suppose that there is a set function 
such that the sequence 
-converges to 
with respect to a single -sequence. Then there is a meager subset such that for each 
the real-valued set functions , , are uniformly -bounded (with respect to 
). Moreover the ’s are uniformly -bounded.
Proof: Observe that, since the ’s are equibounded and -triangular, for every the functions , , are real-valued, -triangular and , and hence -bounded on , thanks to [8, Theorem 3.2]. Moreover there is an -sequence such that for every and there is 
with 
for all 
. By the Maeda-Ogasawara-Vulikh representation theorem (see also [6]) there is a meager set 
, such that the sequence 
is an -sequence in 
for each 
. Thus for every and there is with
(6)
for each and . This implies that 
for any and . Thus for such 
’s the real-valued set functions satisfy the hypotheses of the Brooks-Jewett-type theorem (see also [2]), and so they are uniformly -bounded. This concludes the first part of the assertion.
Now we prove that the set functions , , are uniformly -bounded. Pick arbitrarily any disjoint sequence in and let us show that
(7)
As the set functions are uniformly -bounded for any , where 
is as in (6), it is
(8)
for all . As any countable union of meager subsets of is still meager, then there is a meager subset 
of , without loss of generality containing , such that for any 
and 
it is
(9)
From (8) and (9) it follows that
(10)
for every . Thus, (7) follows from (10) and a density argument. From (7) we deduce that 
, that is 
. Hence, by arbitrariness of the chosen sequence , the ’s are uniformly -bounded.
4. Conclusions
We proved a Brooks-Jewett-type theoremfor Dedekind complete lattice group-valued k-triangular set functions, not necessarily finitely additive, extending [5, Theorem 3.1]. We used the corresponding classical results for real-valued set functions. Note that, in the non-additive setting, boundedness of a set function is not sufficient to have 
-boundedness or -boundedness of its real-valued "components". So, we dealt with the disjoint variation of a lattice group-valued set function and we studied the property 
(bounded disjoint variation). We showed that there exist bounded monotone k-triangular set functions not and not finitely additive, that there are bounded monotone k-triangular set functions satisfying
but not finitely additive, that property is a sufficient but not necessary condition for -boundedness and allows to prove our Brooks-Jewett-type theorem without assuming finite additivity. Furthermore, we proved that our setting includes the finitely additive case, since every bounded finitely additive lattice group-valued set function satisfies property 
Prove similar results with respect to other kinds of convergence.
Prove other types of limit theorems in different abstract contexts.
Prove some kinds of limit theorems without assuming condition 
.
Acknowledgments
Our thanks to the referee for his/her helpful suggestions.
This work was supported by University of Perugia and the Italian National Group of Mathematical Analysis, Probability and Applications (G.N.A.M.P.A.).
References
