| 1. | ||
| 2. | ||
| 3. | ||
| 4. | ||
| 5. | ||
Solution Wave Equation and Parametric Structural Schematic Diagrams of Electromagnetoelastic Actuators Nano- and Microdisplacement
Sergey M. Afonin
Department of Intellectual Technical Systems, National Research University of Electronic Technology (MIET), Moscow, Russia
Email address
Citation
Sergey M. Afonin. Solution Wave Equation and Parametric Structural Schematic Diagrams of Electromagnetoelastic Actuators Nano- and Microdisplacement. International Journal of Mathematical Analysis and Applications. Vol. 3, No. 4, 2016, pp. 31-38.
Abstract
Solution wave equation, structural-parametric models and parametric structural schematic diagrams of electromagnetoelastic actuators are obtained, its transfer functions are bult. Effects of geometric and physical parameters of electromagnetoelastic actuators and external load on its dynamic characteristics are determined. For calculation of control systems with piezoactuators the parametric structural schematic diagrams and the transfer functions of piezoactuators are obtained.
Keywords
Wave Equation, Electromagnetoelastic Actuators, Deformation, Parametric Structural Schematic Diagrams, Nano- and Microdisplacement
1. Introduction
For microelectronics, nanobiology, nanotechnology, nanobiology, power engineering, microelectronics, astronomy for large compound telescopes, antennas satellite telescopes and adaptive optics equipment is promising for use robotics and mechatronics systems with electromechanical actuators based on electromagnetoelasticity (piezoelectric, piezomagnetic, electrostriction, and magnetostriction effects). Piezoelectric actuator (piezoactuator) - piezomechanical device intended for actuation of mechanisms, systems or management based on the piezoelectric effect, converts electrical signals into mechanical movement or force. Piezoactuators are used in the majority of nanomanipulators for scanning tunneling microscopes (STMs), scanning force microscopes (SFMs), and atomic force microscopes (AFMs) [1−26].
By solving the wave equation with allowance for the corresponding equations of the electromagnetoelasticity, the boundary conditions on loaded working surfaces of a actuator, and the strains along the coordinate axes, it is possible to construct a structural parametric model of the electromagnetoelastic actuator. The transfer functions and the parametric structure scheme of the piezoactuator are obtained from a set of equations describing the corresponding structural parametric model of the piezoelectric actuator for control systems.
2. Solution Wave Equation
For constructing a structural parametric model of the electromagnetoelastic actuators nano- and microdisplacement, let us solve simultaneously the wave equation, the equation of the electromagnetoelasticity, and the equations of forces acting on faces of the actuator.
Deformation of the piezoactuator corresponds to its stressed state. If the mechanical stress 
is created in the piezoelectric element, the deformation 
is formed in it. There are six stress components 
, 
, 
, 
, 
, 
, the components - are related to extension-compression stresses, - to shear stresses.
The matrix state equations [7] connecting the electric and elastic variables for polarized ceramics have the form
, (1)
. (2)
Here, the first equation describes the direct piezoelectric effect, and the second - the inverse piezoelectric effect; 
is the column matrix of relative deformations; 
is the column matrix of mechanical stresses; 
is the column matrix of electric field strength along the coordinate axes; 
is the column matrix of electric induction along the coordinate axes; 
is the elastic compliance matrix for 
; and 
is the transposed matrix of the piezoelectric modules. In polarized ceramics PZT there are five independent components 
, 
, 
, 
, 
in the elastic compliance matrix for polarized piezoelectric ceramics, three independent components of the piezoelectric modules 
, 
, 
in the transposed matrix of the piezoelectric modules and three independent components of the dielectric constants 
, 
, 
in the matrix of dielectric constants.
The direction of the polarization axis Р, i.e., the direction along which polarization was performed, is usually taken as the direction of axis 3 for the longitudinal and transverse piezoelectric effects.
The generalized electromagnetoelasticity equation of the actuator [7] has the form
, (3)
where 
is the relative deformation along the axis i, E is the electric field strength, H is the magnetic field strength, 
is the temperature, 
is the elastic compliance for , 
, 
, 
is the mechanical stress along the axis j, 
is the piezomodule, i.e., the partial derivative of the relative deformation with respect to the electric field strength for constant magnetic field strength and temperature, i.e., for , , 
is the electric field strength along the axis m, 
is the magnetostriction coefficient, 
is the magnetic field strength along the axis m, 
is the coefficient of thermal expansion, 
is deviation of the temperature from the value , i = 1, 2, …, 6, j = 1, 2, …, 6, m = 1, 2, 3.
For the electric and magnetic fields acting on the electromagnetoelastic actuator separately, we have equations:
the equation of inverse piezoelectric effect:
for the longitudinal deformation when the electric field along axis 3 causes deformation along axis 3,
for the transverse deformation when the electric field along axis 3 causes deformation along axis 1,
for the shift deformation when the electric field along axis 1 causes deformation in the plane perpendicular to this axis,
the equation of magnetostriction:
for the longitudinal deformation when the magnetic field along axis 3 causes deformation along axis 3,
for the transverse deformation when the magnetic field along axis 3 causes deformation along axis 1,
for the shift deformation when the magnetic field along axis 1 causes deformation in the plane perpendicular to this axis.
Let us consider the longitudinal piezoelectric effect in a piezoactuator shown in Fig. 1, where 
is the thickness. The electrodes deposited on its faces perpendicular to axis 3, the area of face is equal to 
. The equation of the inverse longitudinal piezoelectric effect [6, 7] has the following form:
, (4)
Here, 
is the relative displacement of the cross section of the piezoactuator, is the piezomodule for the longitudinal piezoelectric effect, 
is the electric field strength, 
is the voltage between the electrodes of actuator, is the thickness, is the elastic compliance along axis 3, and is the mechanical stress along axis 3.
The equation of equilibrium for the forces acting on the piezoactuator (piezoelectric plate) can be written as
(5)
where F is the external force applied to the piezoactuator, is the cross section area and M is the displaced mass.
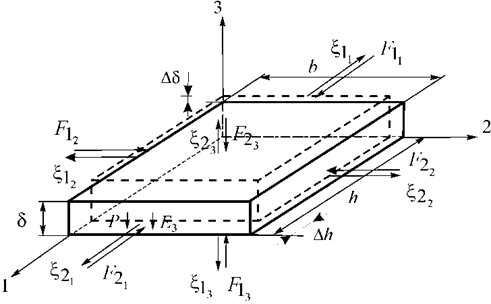
Fig. 1. Piezoactuator.
Let us solve simultaneously the wave equation, the equation of the inverse longitudinal piezoelectric effect, and the equation of forces acting on the faces of the piezoactuator for constructing a structural parametric model of the voltage-controlled piezoactuator.
Calculations of the piezoactuators are performed using a wave equation [5−7] describing the wave propagation in a long line with damping but without distortions, which can be written as
, (6)
where 
is the displacement of the section of the piezoelectric plate, x is the coordinate, t is time, 
is the sound speed for , 
is the damping coefficient that takes into account the attenuation of oscillations caused by the energy dissipation due to thermal losses during the wave propagation.
Using the Laplace transform, we can reduce the original problem for the partial differential hyperbolic equation of type (6) to a simpler problem for the linear ordinary differential equation [8,9] with the parameter of the Laplace operator p.
Applying the Laplace transform to the wave equation (6)
, (7)
and setting the zero initial conditions,
. (8)
We obtain the linear ordinary second-order differential equation with the parameter p written as
, (9)
with its solution being the function
, (10)
where 
is the Laplace transform of the displacement of the section of the piezoelectric actuator, 
is the propagation coefficient. Determining coefficients C and B from the boundary conditions as
for 
(11)
for 
Then, the constant coefficients
, 
. (12)
Then, the solution (9) of the linear ordinary second-order differential equation can be written as
. (13)
The equations for the forces operating on the faces of the piezoelectric actuator plate are as follows:
for , (14)
for ,
where 
and 
are determined from the equation of the inverse piezoelectric effect.
For and , we obtain the following set of equations for determining stresses in the piezoactuator:
, (15)
.
Equations (14) yield the following set of equations for the structural parametric model of the piezoactuator:
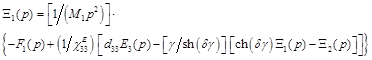, (16)
,
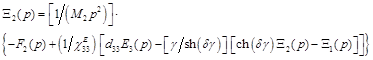where 
.
Figure 2 shows the parametric structural schematic diagram of a voltage-controlled piezoactuator corresponding to the set of equations (16), this diagram supplemented with an external circuit equation 
, where 
is the supply voltage, R is the resistance of the external circuit, and 
is the static capacitance of the piezoactuator.
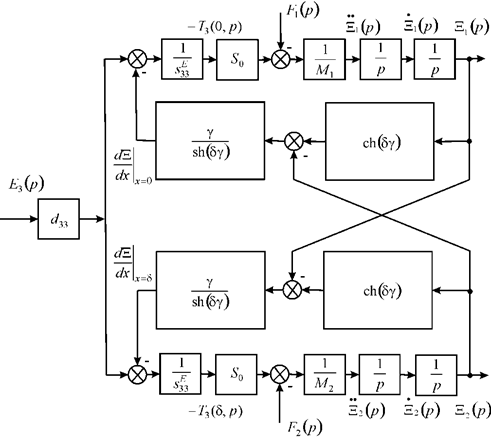
Fig. 2. Parametric structural schematic diagram of a voltage-controlled piezoactuator for longitudinal piezoelectric effect.
The equation of the inverse piezoelectric effect [6,7] for the transverse strain in the voltage-controlled piezoactuator
(17)
where 
is the relative displacement of the cross section along axis 1, is the piezomodule for the transverse piezoeffect, 
is the electric field strength along axis 3, is the elastic compliance along axis 1, and is the mechanical stress along axis 1.
The wave equation of the piezoactuator can be written as equation (6). Then, the solution of the linear ordinary differential equation (9) can be written as (10), where the constants C and B for this solution are determined from the boundary conditions as
for , (18)
for 
,
, 
. (19)
Then, the solution (10) can be written as
(20)
The equations of forces acting on the faces of the piezoelectric actuator are as follows:
for x = 0, (21)
for x = h,
where 
and 
are determined from the equation of the inverse piezoelectric effect. Thus, we obtain the following set of equations for mechanical stresses in the piezoactuator at and
(22)
The set of equations (22) for mechanical stresses in piezoactuator yields the following set of equations describing the structural parametric model of piezoactuator for the transverse piezoelectric effect
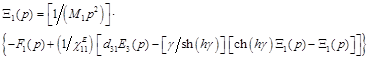, (23)
,
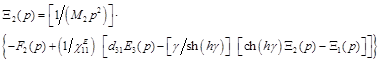where 
.
We obtain the set of equations (23) describing the structural parametric model of piezoactuator and parametric structural schematic diagram of a voltage-controlled piezoactuator for transverse piezoelectric effect on Figure 3,
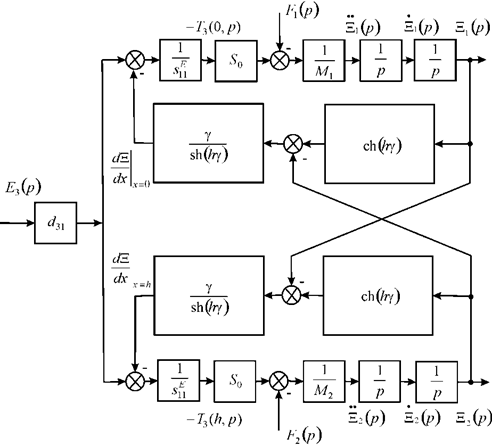
Fig. 3. Parametric structural schematic diagram of a voltage-controlled piezoactuator for transverse piezoelectric effect.
Taking into account generalized electromagnetoelasticity equation (3), we obtain the following system of equations describing the generalized structural-parametric model of the electromagnetoelastic actuators nano- and microdisplacement for the control systems in the following form:
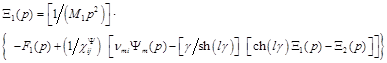, (24)
,
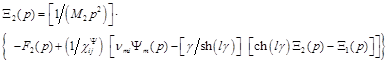where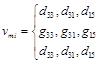 
, 
, 
, 
, 
, 
, 
,
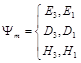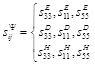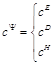then parameters 
of the control for the electromagnetoelastic actuator: E for voltage control, D for current control, H for magnetic field strength control. Figure 4 shows the generalized parametric structural schematic diagram of the electromagnetoelastic actuator corresponding to the set of equations (24).
Generalized structural-parametric model (24) of the electromagnetoelastic actuators nano- and microdisplacement after algebraic transformations provides the matrix transfer functions of the electromagnetoelastic actuator in the form of the ratio of the Laplace transform of the displacement of the actuator face and the Laplace transform of the corresponding parameter at zero initial conditions.
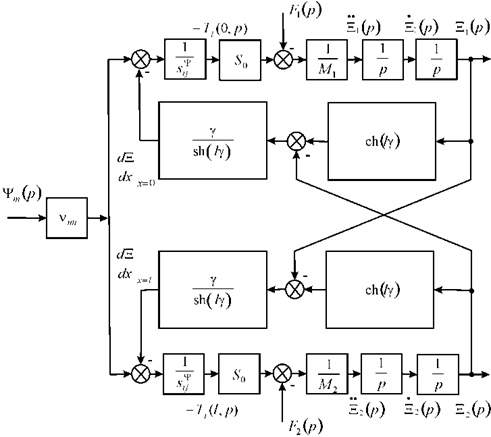
Fig. 4. Generalized parametric structural schematic diagram of the electromagnetoelastic actuator.
3. The Transfer Functions of the Electromagnetoelastic Actuators
The joint solution of equations (24) for the Laplace transforms of displacements of two faces of the electromagnetoelastic actuator yields
, (25)
,
where the generalized transfer functions of the electromagnetoelastic actuator are
,
,
,
,
,
.
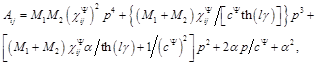
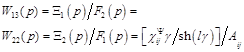Therefore, we obtain from equations (25) the generalized matrix equaion for the electromagnetoelastic actuator nano- and microdisplacement in the matrix form for the control systems.
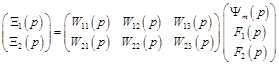. (26)
Let us find the displacement of the faces the electromagnetoelastic actuator in a stationary regime for 
, 
and inertial load. The static displacement of the faces the electromagnetoelastic actuator 
and 
can be written in the form:
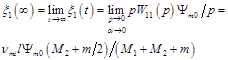, (27)
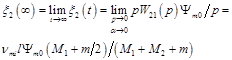, (28)
, (29)
where 
is the mass of the electromagnetoelastic actuator, 
are the load masses.
Let us consider a numerical example of the calculation of static characteristics of the piezoactuator from piezoceramics PZT under the longitudinal piezoelectric effect at 
and 
. For 
m/V, 
V, 
kg and 
kg we obtain the static displacement of the faces of the piezoactuator 
nm, 
nm, 
nm.
The static displacement the faces of the piezoactuator for the transverse piezoelectric effect and inertial load at 
, 
and can be written in the following form:
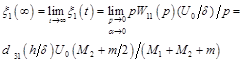, (30)
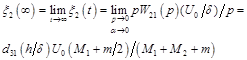, (31)
. (32)
The static displacement of the faces of the piezoactuator for the transverse piezoelectric effect and inertial load at and
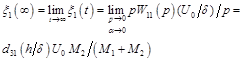, (33)
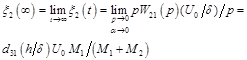. (34)
Let us consider a numerical example of the calculation of static characteristics of the piezoactuator from piezoceramics PZT under the transverse piezoelectric effect at and . For 
m/V, 
m, 
m, 
V, kg and kg we obtain the static displacement of the faces of the piezoelectric actuator 
nm, 
nm, 
nm.
Let us consider the description of the piezoactuator for the longitudinal piezoelectric effect for one rigidly fixed face of the transducer at 
, therefore, we obtain from equation (25) the transfer functions of the piezoactuator for the longitudinal piezoelectric effect in the following form:
, (35)
We obtain the expression the transfer function in the frequency range of 
, using the approximation of the hyperbolic cotangent by two terms of the power series in transfer functions (35), at in the form:
, (36)
, 
, 
.
where 
is the time constant and 
is the damping coefficient, 
- is the is rigidity of the piezoactuator under the longitudinal piezoeffect.
4. The Main Results
Taking into account equation of generalized electromagnetoelasticity (piezoelectric, piezomagnetic, electrostriction, and magnetostriction effects) and decision wave equation we obtain a generalized parametric structural schematic diagram of electromagnetoelastic actuator Figure 4 and generalized transfer functions for the control systems. The results of constructing a generalized structural-parametric model and parametric structural schematic diagram of electromagnetoelastic actuator for the longitudinal, transverse and shift deformations are shown in Figure 4. Parametric structural schematic diagrams piezoactuators for longitudinal piezoeffect Figure 2 and for transverse piezoeffect Figure 3 converts to generalized parametric structural schematic diagram of the electromagnetoelastic actuator Figure 4 with the replacement of the parameters
, 
, 
, 
.
Generalized structural-parametric model and generalized parametric structural schematic diagram of the electromagnetoelastic actuator after algebraic transformations provides the transfer functions of the electromagnetoelastic actuators nano- and microdisplacement for communications systems.
The piezoactuator with the transverse piezoelectric effect compared to the piezoactuator for the longitudinal piezoelectric effect provides a greater range of static displacement and less working force.
Using the solutions of the wave equation of the electromagnetoelastic actuator and taking into account the features of the deformations along the coordinate axes, it is possible to construct the generalized structural-parametric model, generalized parametric structural schematic diagram and the transfer functions of the electromagnetoelastic actuator for control systems.
5. Conclusions
Using the obtained solutions of the wave equation and taking into account the features of the deformations along the coordinate axes, it is possible to construct the generalized structural-parametric model and parametric parametric structural schematic diagram of the electromagnetoelastic actuator and to describe its dynamic and static properties with allowance for the physical properties, the external load during its operation as a part of the control systems.
The parametric structural schematic diagrams and the transfer functions of the piezoactuators for the longitudinal and transverse piezoeffects are obtained from structural parametric models of the piezoactuators.
References
