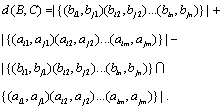The sequence distance is a way to measure an individual's ranking difference in the two sequences, and then we need to calculate the sum of all the individual ranking deviations, which is then used to measure the distance of two sequences.
This paper presents a new definition and proofs regarding the inverse number sequence distance. We have been solved minimum violation ranking scheduling problems through a contrastive analysis of the solution space, which the inverse number sequence distance and the absolute value sequence distance method are applied. We have continued the analysis of the advantages and disadvantages, and finally used a gravity optimization algorithm to calculate the optimal solution.
2. Data Representation
Sequence distance can take many forms, such as matrix expression or vector expression.
2.1. Pairwise Comparison Matrix Expression Form
The distance of matrix expression between the two objects is a kind of common sequence data expression. Through the comparison between the two matrix, then we use 0, 1 to represent the relationship of the two respectively. As shown below:
 .
.
If there are n variables, there are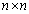 pairs to compare, which will make up the comparison matrix
pairs to compare, which will make up the comparison matrix 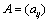 .
.
2.2. Vector Expression
For vector expression 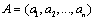 ,
, 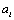 represents the i-th variable location in the sequence. For example, let's assume that the variables of sequence A are: a, b, c, and d in turn; then
represents the i-th variable location in the sequence. For example, let's assume that the variables of sequence A are: a, b, c, and d in turn; then 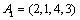 represents that a is in second place, b is in first place, c is in fourth place, and is in third place. Yet
represents that a is in second place, b is in first place, c is in fourth place, and is in third place. Yet 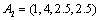 represents that a is in first place, b is in fourth place, and c and d are in second and third place together.
represents that a is in first place, b is in fourth place, and c and d are in second and third place together.
3. Sequence Model of the Preference
3.1. Inverse Number Definition
In advanced algebra [14-16], arrangement and inverse number is defined as following:
Arrangement: a sequence array that consists of 1, 2,..., n is called an n-level arrangement.
Inverse number: if the position sequence of two numbers is in contrast to their size order in a sequence, it is an inverse order. The total number of inverse order in a sequence is called the inverse number of sequence.
We have a new understanding of the above two definitions. In actuality, an inverse number is the sum of the inverse order that compares the position of each number in a random arrangement relative to the natural order n (1, 2,..., n). An inverse order can be eliminated by a data exchange. Suppose now we get the inverse number of the two random arrangements n1, n2 relative to the natural order n(notes for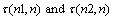 ). If
). If 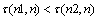 , then n1 requires less change than n2 to become a natural number sequence. So the inverse number of two sequences can be called as their distance. Consequently, it can be said that the distance between n1 and n is closer than the distance between n2 and n.
, then n1 requires less change than n2 to become a natural number sequence. So the inverse number of two sequences can be called as their distance. Consequently, it can be said that the distance between n1 and n is closer than the distance between n2 and n.
Obviously, the arrangement of the data defined above does not contain the same data. We have promoted a method that calculates the inverse number of the number sequence: a random number sequence for which the length is n and a natural number sequence that is then applied to any two number sequence. We established a natural number sequence firstly according to the element position information of one array; then we have built an number sequence according to the relative information of the element location for the other array. The result that occurs is a situation like a random number sequence for which the length is n and a natural number sequence; we then used this method to calculate their inverse number. A concrete example is shown in Figure 1: (M represents the inverse number sequence distance of two arrangements).

Figure 1. Relativeinverse number concept map.
3.2. Based on the CS Vector Mode Preference Sequence Distance Meet the Conditions
According to the different ordinal preference expression forms, Cook and Seiford have provided several measurement methods of the ordinal preference distance when working with group decision-making problems, and put forward some conditions that the sequencing vector distance measurement function must satisfy. These conditions are called the CS mode:
Suppose the sorting vectors are as follows:
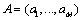 ,
, 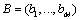 ,
, 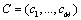
Where 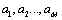 ,
, 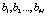 and
and 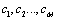 are both a full permutation for which that number is between 1 and M;
are both a full permutation for which that number is between 1 and M;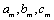 all represent the ranking position of the scheme
all represent the ranking position of the scheme 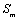 ;
; 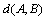 is a distance measure function of sorting vector
is a distance measure function of sorting vector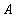 and sorting vector
and sorting vector . Cook and Seiford think
. Cook and Seiford think  should meet the following conditions:
should meet the following conditions:
Condition 1: 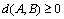 .
. 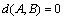 if and only if
if and only if 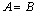 .
.
Condition 2: 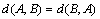 .
.
Condition 3: 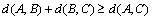 .
.
Condition 4: 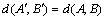 , when
, when 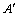 and
and 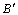 are the new formation of the sequencing vector after
are the new formation of the sequencing vector after 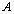 and
and 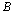 make the same ranking transfer.
make the same ranking transfer.
Condition 5: 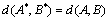 , when
, when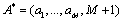 ,
, 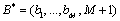 .
.
Condition 6: The minimum effective distance between the sequences is 1.
Seiford and Cook proved that only sequence distance measure that meets the sixth conditions is:
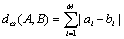 .
.
3.3. Proof Process of the Inverse Number Sequence Distance Satisfies the Conditions
Condition 1: 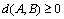 .
. 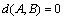 if and only if
if and only if 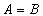 .
.
Proof: Obviously, according to the definition of inverse number we can get: 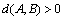 , for all the A and B;
, for all the A and B;
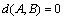 if and only if
if and only if 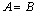 .
.
Sufficiency: When A = B, the elements in the sequence A and B have the same location; then 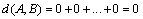 .
.
Necessity: proof by contradiction. Suppose A≠B, where 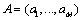 ,
, 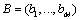 , elements
, elements 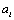 of sorting A are integers between 1 and M, and elements
of sorting A are integers between 1 and M, and elements 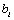 of sorting B are integers between 1 and M.
of sorting B are integers between 1 and M.
When A≠B, there are at least two numbers in A whose positions change relative to B, so 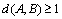 , and
, and 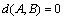 contradictions. Therefore, when
contradictions. Therefore, when 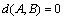 , A=B.
, A=B.
Condition 2: 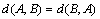 .
.
Proof: Let's use a mathematical induction to prove that the relative inverse number of any two sorting in stances is equal.
When 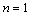 , it is clearly established.
, it is clearly established.
When 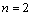 , if A, B are the same, then the inverse number is 0.
, if A, B are the same, then the inverse number is 0.
If A, B are different, assume 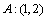 ,
, 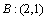 , then
, then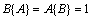 ;
; 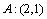 ,
, 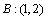 .
.
Suppose when the series is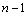 , a conclusion is established. Namely, the inverse number of
, a conclusion is established. Namely, the inverse number of 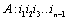 and
and 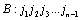 for each other is
for each other is 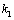 .
.
When the series is n,we added element t; its position in A is x and in B is y, then:
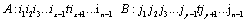 .
.
If 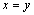 ,
, 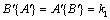 . Do not break general,assume
. Do not break general,assume 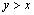 ,
,
(1) 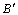 relative to
relative to 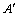 ,
, 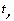 and
and 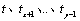 constitutes an inverse order, then
constitutes an inverse order, then 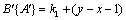 .
.
(2) 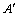 relative to
relative to 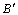 ,
, 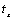 and
and 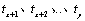 constitutes an inverse order, then
constitutes an inverse order, then 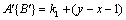 .
.
Therefore, proposition 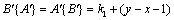 is founded.
is founded.
Condition 3: 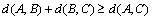 .
.
Proof: Assume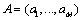 ,
, 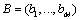 ,
,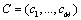 . For the three sequences contain in different elements, we ruled the sorting of elements in A as a standard order. Then:
. For the three sequences contain in different elements, we ruled the sorting of elements in A as a standard order. Then:
The inverse orders of 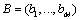 are
are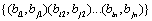 .
.
The inverse orders of 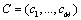 are
are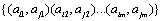 .
.
So 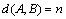 ;
; 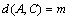 .
.
(1) When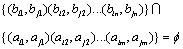 ,
,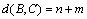 .
.
(2) When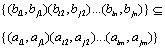 ,
, 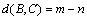 .
.
(3) When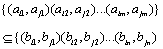 ,
, 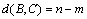 .
.
(4) When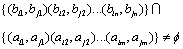 ,
,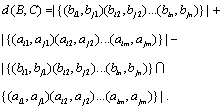
So we have obtained: 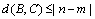 .
.
Therefore, when 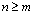 ,
, 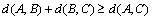 ; when
; when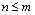 ,
, 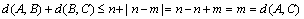 . Namely
. Namely 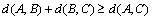 is founded.
is founded.
Condition 5: 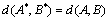 , when
, when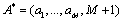 ,
, 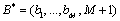 .
.
Proof: 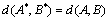 , when
, when 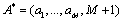 ,
,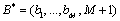 .
.
Assume: 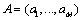 ,
, 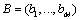 ; we ruled the sorting of elements in A as a standard order. Then the inverse number of
; we ruled the sorting of elements in A as a standard order. Then the inverse number of 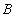 is n, and its set is
is n, and its set is 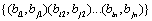 .
.
We added an element of M + 1 in the end of sequence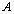 , then
, then 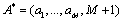 . We also ruled the sorting of elements in A as a standard order. In addition, we added an element of M + 1 to the end of sequence
. We also ruled the sorting of elements in A as a standard order. In addition, we added an element of M + 1 to the end of sequence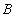 , then
, then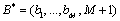 . Because the position of the previous elements had not changed, the inverse orders of
. Because the position of the previous elements had not changed, the inverse orders of 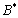 were also
were also 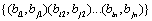 , but there was no inverse order for M + 1 and the rest of the elements. Therefore,
, but there was no inverse order for M + 1 and the rest of the elements. Therefore, 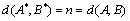 .
.
Condition 6: Minimum effective distance between the sequences is 1.
Proof: Assume 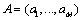 ; clearly, there must be a sequence
; clearly, there must be a sequence 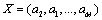 . Then the inverse order of sequence X on the basis of sequence A is
. Then the inverse order of sequence X on the basis of sequence A is 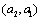 ,so there must be a minimum effective distance d = 1 in any sequence.
,so there must be a minimum effective distance d = 1 in any sequence.
4. Application Example
4.1. Data Form of Expression
We consider a minimum violations ranking problem that contains six variable sequences. In order to express this more easily, this example's data uses the vector expression form. Now suppose there are six variables: a, b, c, d, e, f, and there are two sortings: 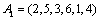 and
and 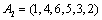 . In order to stay in line with the following expression, the sorting sequence is shown in the table below:
. In order to stay in line with the following expression, the sorting sequence is shown in the table below:
Table 1. Exampleinitial sequence.
4.2. Preference Distance to Find the Optimal Solution
We have found that the solution of the inverse number sequence distance and Euclidean distance, respectively, by using the traversal method. As shown in the figure below, the X-axis represents the sequence, and the y-axis represents the sum of the distance between the sequence and the above two sequences.
Through the two images above, it is evident that two of the solution spacesin the distance of the overlap degree are high.An inverse number sequence distance can be obtained from the optimal solution for 176, the absolute value distance ofthe optimal solution for 228. Among them, the common optimal solution number is 96. Yet, the inverse number sequence distance in common proportion to the optimal solution is 68.8%, and the absolute distance is 42.0%. The two distances explain the sequence distance from different angles, but it can be seen from the data that the inverse number sequence distance explains the distance of the sequence more fully than the absolute distance; the hit rate is relatively higher.
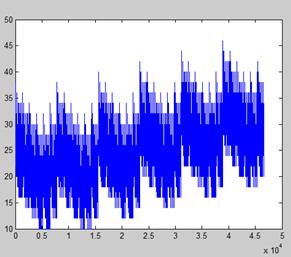
Figure 2. Inverted number distance solution space diagram.
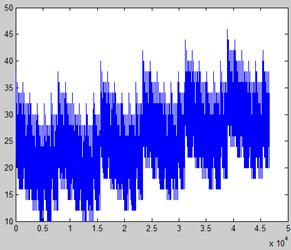
Figure 3. Absolute value distance solution space diagram.
4.3. Borda Method
This method was put forward by Borda and includes a detailed analysis by Kendall; the main idea is to calculate the sum of each variable assigned to the sorting order. If there are three variables, a, b, c, and there are 60 people voting to sort these three variables, the final results in Table 2 shows:
Table 2. The Borda algorithm example data.
| | Variable scores |
| Votes | a | b | c |
| 23 | 1 | 2 | 3 |
| 17 | 3 | 1 | 2 |
| 2 | 2 | 1 | 3 |
| 10 | 2 | 3 | 1 |
| 8 | 3 | 2 | 1 |
Each variable total score should be:
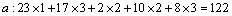
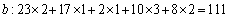
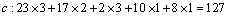
So the result is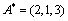 using the Borda method. The absolute value obtains 176 optimal solutions, but we can use the Borda method to get an optimal solution. The obtained results are as follows:
using the Borda method. The absolute value obtains 176 optimal solutions, but we can use the Borda method to get an optimal solution. The obtained results are as follows: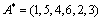 .
.
5. Gravitation Search Algorithm
5.1. The Implementation Process of the Algorithm
Firstly, we randomly initialized the particle's position and speed to calculate each particle's fitness function, and then calculate the inertial mass according to the fitness of each particle, calculating the best value of inertial mass and the worst value. Secondly, we calculated the gravity on each particle in each dimension, solving for gravitational acceleration. Finally, we updated the particle's position and speed in circulation to find the final result. Specific steps are as follows:
(1) Identify the search space.
(2) Random initialization.
(3) Calculate the particle's fitness.
(4) Update the gravity coefficient G(t), the best value best(t), the worst value worst(t), and the inertial mass of particles.
(5) Calculate the sum of the force in all directions.
(6) Calculate the acceleration and speed.
(7) Update the positions of the particles.
(8) Return to step (3), loop iteration until it meets either the requirements of cycles or precision.
(9) End of cycle, output the result.
5.2. Application of Gravitational Search Algorithm
In the process of using a method to solve the inverse number distance, the optimal solution that we search is the sequence for which the sum of the distance is the shortest among all other sequences. When lesser elements are in the sequence, however, we can use a traversing method, by gradually ordering of all possible traverses to find the optimal solution. However, the complexity of the algorithm is O(n!), so we cannot use this method to find the optimal solution when n is too large.
We have used a gravitational search algorithm (this algorithm can determine one of the optimal solution, but does not determine all optimal solutions like the traverse method). After a certain number of sequences, though, we can use the search algorithm to solve the inverse number distance.
However, the gravitational search algorithm is used in continuous data, and the inverse number sequence distance that we have defined is discrete data, which is between 1 and n; consequently, the algorithm should be improved once more while we are in the application. The improved aspects are as follows:
(1) When initializing the solution space, the random number is between 1 and n.
(2) An update particle is given a serial number according to the size of its location in solving the process of iteration.
(3) A new position matrix carries on the iteration as well.
Through these improvements, eventually we will obtain the optimal solution.
5.3. Numerical Example
Let's assume that we have three initial sequence as following, and the sorting is from 1 to 10, respectively.
Table 3. Example data of gravitation algorithm.
| 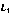
| 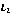
| 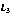
| 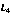
| 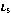
| 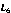
| 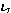
| 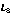
| 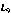
| 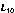
|
| 2 | 5 | 7 | 8 | 1 | 3 | 9 | 4 | 10 | 6 |
| 1 | 3 | 9 | 2 | 6 | 4 | 5 | 8 | 7 | 10 |
| 5 | 6 | 2 | 9 | 3 | 8 | 4 | 1 | 7 | 10 |
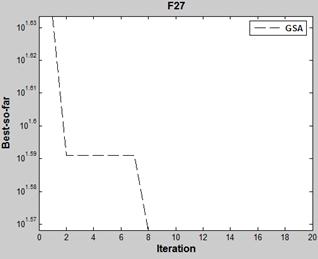
Figure 4. Gravitation solving iterative process.
One of the most optimal sequences is obtained by using the above methods as shown in Table 4, The optimal solution is obtained by using the iterative method as shown in Table 5.
Table 4. Optimal solution of gravitation algorithm.

Table 5. Optimal results of Iteration.

The gravity algorithm only needs 8 iterations get the optimal solution; it is accurate that here there is only areversal of two pairs of numbers, compared with the optimal solution of the iterative method. Thus, the gravity optimization algorithm not only demonstrates superior performance in computing time, but also provides precise results.
6. Conclusion
This paper established a sequence distance that was defined based on minimum violation rankings. Relative to the absolute value, when using the distance to solve the problem of the real preference, this definition of the distance is better than Cook and others. But there are still some problems that leave room for subsequent improvement: inverse number distances consider the position between the two variables to be opposite from each other without considering to what extent the inverse order compares the gap between the two, and cannot reflect completely information regarding voter preference (e.g., degree of preference), consequently providing no quantitative consideration.
Acknowledgements
We would like to thank the National Natural Science Foundation of China (No. 11401115, 11471012), the Project of Department of Education of Guangdong Province (No. 13KJ0396), and Science and Technology Program of Guangzhou, China (No. 2013B051000075).
References
- I. Ali, W.D. Cook, M. Kress, On the minimum violations ranking of a tournament, Management Science 32 (6) (1986) 660–672.
- S.T. Goddard, Ranking tournaments and group decision making, Management Science 29 (12) (1983) 1384–1392.
- J. Moon, Topics on Tournaments, Holt, Reinhart and Winston, New York, 1968.
- Ma, Li-Ching. A new group ranking approach for ordinal preferences based on group maximum consensus sequences. EUROPEAN JOURNAL OF OPERATIONAL RESEARCH. MAY 16 2016 251(1): 171-181.
- Branke, J. Corrente, S. Greco, S. Slowinski, R; Zielniewicz, P.Using Choquet integral as preference model in interactive evolutionary multiobjective optimization. EUROPEAN JOURNAL OF OPERATIONAL RESEARCH. MAY 1 2016, 250(3):884-901.
- J.M. Blin. A linear assignment formulation of the multiattribute decision problem, Review Automatique,InformatiqueetRechercheOperationnelle 10(6) (1976) 21–23.
- Cook, Wade D.; Golany, Boaz; Penn, Michal. Creating a consensus ranking of proposals from reviewers' partial ordinal rankings COMPUTERS & OPERATIONS RESEARCH,. 2007, 34(4): 954-965.
- Teresa Escobar, Maria; Aguaron, Juan; Maria Moreno-Jimenez, Jose. Some extensions of the precise consistency consensus matrix.DECISION SUPPORT SYSTEMS. JUN 2015,74: 67-77.
- Chen, Yen-Liang; Cheng, Li-Chen; Huang, Po-Hsiang. Mining consensus preference graphs from users' ranking data.DECISION SUPPORT SYSTEMS. JAN 2013,54(2): 1055-1064.
- W.D. Cook, L. Seiford, S. Warner, Preference ranking models: Conditions for equivalence, Journal of Mathematical Sociology, 9(1983) 125–127.
- J. Deegan, E. Packel, A new index of power for simple n-person games, International Journal of Game Theory, 7 (1979) 99–131.
- M. DeGroot, Reaching a consensus, Journal of the American Statistical Association 69 (1974) 118–121.
- W.D. Cook, L. Seiford, Priority ranking and consensus formation, Management Science 24 (16) (1978) 1721–1732.
- Greco, Salvatore; Kadzinski, Milosz; Mousseau, Vincent.Robust ordinal regression for multiple criteria group decision: UTA(GMS)-GROUP and UTADIS(GMS)-GROUP. DECISION SUPPORT SYSTEMS. FEB 2012,52(3):549-561.
- Ma, Li-Ching; Li, Han-Lin. Using Gower Plots and Decision Balls to rank alternatives involving inconsistent preferences. DECISION SUPPORT SYSTEMS. JUN 2011,51(3): 712-719.
- J.C. Borda, Memoire sur les elections au scrutin, Histoire de lAcademie Royale de Science, Paris, 1981.

 (Zhenyou Wang)
(Zhenyou Wang)