On Solution Space of Intelligent Tutoring Systems for Programming: A Review

Hieu Bui

Faculty of Information Technology, Ho Chi Minh City University of Transport, Ho Chi Minh City, Vietnam

Email address

Citation

Hieu Bui. On Solution Space of Intelligent Tutoring Systems for Programming: A Review. American Journal of Computer Science and Information Engineering. Vol. 3, No. 2, 2016, pp. 7-15.

Abstract

In intelligent tutoring systems (ITSs) for programming, a single programming exercise may produce many alternative solutions from students. It is difficult to build ITSs for programming due to the complexity and variety of possible solutions. In order for the students to learn from the system, it is necessary for them to receive feedback on their solutions to the programming exercises. To provide personalized feedback to students who are solving programming exercises effectively, the ITSs for programming must be able to cover a large space of possible solutions. The goal of this paper is to provide a brief review of the works in the literature related this problem.

Keywords

Solution Space, Intelligent Tutoring System, Intelligent Programming Tutor, Programming Tutor, Programming Tutoring System, Programming, Programming Exercises, Learning Programming, Teaching Programming

1. Introduction

Programming is a useful skill and teaching basics of programming is part of many curricula in universities and higher education. Programming is a fundamental component of any Computer Science curriculum. It is also incorporated into many other disciplines such as Transportation Economics, Construction Economics, Logistics, Electronic Engineering, Transportation Engineering, Marine Engineering, Ship Engineering, Civil Engineering, Mechanical Engineering, Business, Accounting, and many more disciplines due to its widespread use in industry. The best method to learn programming is to write programs. However, programming is a subject that many beginning students find difficult. Also the student groups are large and heterogeneous and thus it is difficult to design the instruction so that it would be beneficial for everyone. This often leads to high drop-out rates on programming courses [19]. Learning how to program is a universal problem that is facing many students in introductory programming courses. This multinational problem created the need for an effective and easy to use learning system [2]. Teaching introductory programming has challenged educators for decades. Of the many suggested methods of improving the teaching process, individual tutoring has proven to be very effective [36]. Since teachers are limited in the amount of time they can spend helping students, an easy to access, automated help source would be a great benefit to students. ITSs are a natural solution to this need, as they are designed to give individualized feedback and assistance to students who are working on problems [31]. An ITS is a computer system that provides immediate and customized instruction or feedback to learners [23]. ITSs for programming are educational systems that teach algorithms or programming languages, usually without intervention from a human teacher [5].

A variety of ITSs for programming have been built to provide tutoring services for programming problems. In this paper, 52 ITSs for programming (Table 1, Table 2 and Table 3) may be divided into three classes: 1) ITSs for curriculum sequencing (class 1), 2) ITSs for analyzing solution (class 2) and 3) ITSs for programming problem solving support (class 3). The goal of ITSs for curriculum sequencing is to provide the student with the most suitable individually planned sequence of programming concepts/topics to learn and learning tasks (examples, questions, etc.) to work with. It helps the student find an "optimal learning path" through the learning material (learning content). In the context of Web-based education, curriculum sequencing technology becomes very important due to its ability to guide the student through the hyperspace of available information. The typical ITSs for programming of this class are No. 12, No. 13 (Table 1), No. 21, No. 22 (Table 2), No. 44 (Table 3). ITSs for analyzing solution deal with students' solutions of programming exercises. Unlike automated grade system which can only tell whether the solution is correct or not, theses ITSs can tell what is wrong or incomplete and which missing or incorrect pieces of knowledge may be responsible for the error. These ITSs can provide the student with extensive error feedback. The typical ITSs for programming of the class 2 are No. 4, No. 5, No. 6, No. 7 (Table 1), No. 23, No. 24, No. 25 (Table 2), No. 45, No. 46, No. 48, No. 51 (Table 3). The goal of ITSs for programming problem solving support is to provide the student with intelligent help on each step of programming problem solving - from giving a hint to executing the next step for the student. The typical ITSs for programming of the class 3 are No. 40, No. 46, No. 47 (Table 3).

Most of the ITSs for programming have been developed to learn to write programs (class 2 and class 3). ITSs for programming are useful first year computer science students and non-major students. When using these systems, most students can remove compilation errors quickly because the errors messages generated by the ITSs for programming are usually very informative. As a consequence, the amount of time students spend on each programming exercise is reduced substantially. Besides, a large number of the students remove the error on their own, which helps in reducing the number of questions asked to the teachers [9].

The major challenge here is even simple programming problems can have multiple separate correct solutions and hundreds of intermediate states, and each of these states can be rewritten in hundreds of ways by varying the code’s ordering or adding extra code. As an example, a simple programming exercise is given: calculate and print the sum of all odd positive numbers under 100. This programming exercise can be solved in multiple ways using constructs of an imperative programming language, for example:

We can also think of many variants for any of these solutions, for example:

In this small example we can already see many syntactic differences, such as:

• Using a while loop instead of a for loop.

• Using a compound assignment operator (counter += 2) instead writing out the full assignment (counter = counter + 2).

• Using a different name for a variable.

We can also identify a minor semantic difference in variant 1: looping until the counter is at least 101 instead of 100. The result is still a correct program. Also, if we swap two independent statements, do we get a different solution? Another issue is performing a calculation in steps instead of in a single assignment and even only printing the expected end result. Are these different solutions or simply variants of the same solution? [17]

One of the main functions of ITSs for programming is providing feedback to hint students solve programming exercises. Understanding solution variation is important for providing appropriate feedback to students [7]. It is necessary that the system be capable of identifying all such variations [36]. The following section presents a brief review of the current studies related to this work.

Table 1. ITSs for programming from 1976 to 1999.

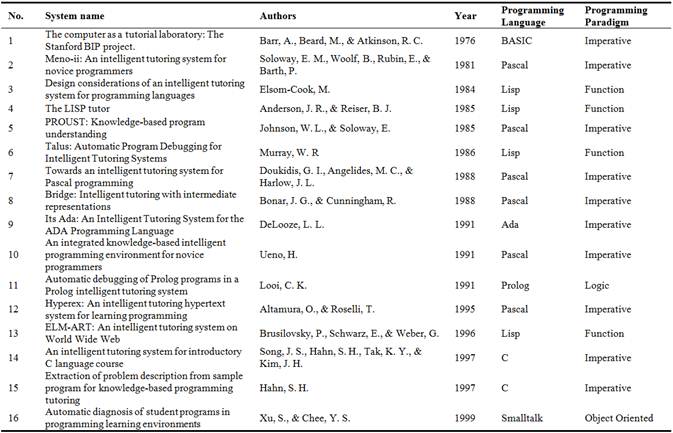
Table 2. ITSs for programming from 2000 to 2010.

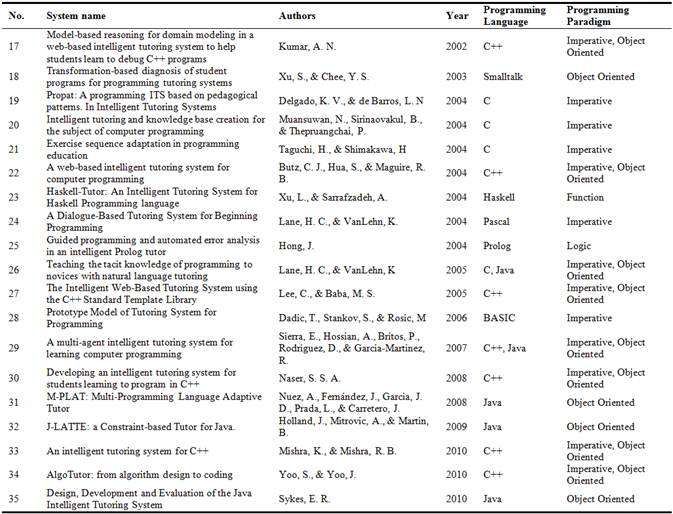
Table 3. ITSs for programming from 2011 to 10/15/2015.

2. Current Approaches

2.1. The Genetic Programming (GP) Approach

A genetic programming algorithm for evolving imperative programs using memory, selection and iterative programming constructs was implemented. The GP approach was able to evolve solution programs for 10 programming problems taken from a first year course on programming [15]. One major drawback of this approach is that able to evolve solution programs for only 10 programming exercises.

2.2. The Deterministic Finite Automaton (DFA) Approach

This approach comprised the following steps:

1.  takes a model program for a programming problem written in C++ (provided by teacher/expert because they are experts in their field and their solutions serve as examples for students) with a number of test cases, cleans up and granulates the model program,

2.  generates all possible variations of the model program,

3.  constructs a DFA from the solution space, taking each solution as a string,

4.  attempts to compare a buggy student program to the finite list of program strings accepted by the problem’s DFA, and

5.  depending on the student’s plan and output correctness, it reports on discovered bugs and suggest repairs or declares the student’s program as correct [1].

The main limitation of DFA, however, is not robust. It is a proof of concept that we have used to demonstrate how a tool can be used to tutor student programmers based on DFAs of alternative solutions and bug detection algorithms.

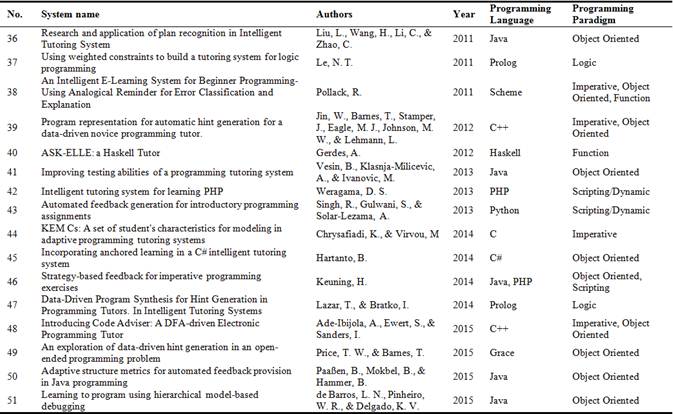
2.3. The Constraint Based Modelling (CBM) Approach

This approach uses constraints to model a space of correct solutions, rather than enumerating them. A constraint represents a domain principle or specifies a property of correct solutions. A set of constraints divides the space of solutions into two subspaces: the inner space for correct and the outer space for incorrect solutions as Figure 1. illustrates. Whenever a solution violates a constraint, that solution falls into the outer space, and a CBM tutoring system derives a feedback associated to that violated constraint [14], [21]. A programming exercise with this approach is that it fails to take the imperative programming languages into account.

Figure 1. A solution space determined by the constraints. Ci: constraint, : space of correct solutions,: space of incorrect solutions.

2.4. The Program Transformation Based Approach

2.4.1. Intelligent Tutoring System for Learning PHP

The system converts the student’s solution into a set of predicates. These predicates are then compared against an overall goal which is also depicted as a set of predicates. Any missing predicates are used to identify sub-goals of the programming exercise that are not met and to provide relevant feedback [17]. The main weakness with this system is that the tutor is not focused on providing feedback during programming.

2.4.2. Intelligent Tutoring Systems for Learning C, Java and PHP

Using programming strategies, in combination with program transformations, three these systems recognizes many different student programs from a limited set of model solutions. Using programming strategies, in combination with program transformations, three these systems recognizes many different student programs from a limited set of model solutions. The distinguishing characteristics of these programming tutors are:

• it supports the incremental development of programs: students can submit incomplete programs and receive feedback and/or hints.

• it calculates feedback automatically based on model solutions to exercises. A teacher does not have to specify feedback the feedback by hand.

• correctness is based on provable equivalence to a model solution, using a normal form for functional programs. If system cannot determine whether or not a program is equivalent to a model solution, system uses testing as an approximation.

• it recognizes arbitrary many student steps on the way to a solution [10], [17], [18].

• One major drawback of these systems is that these ones based on model solutions provide by teachers/experts, because they are experts in their field and their solutions serve as examples for students. However, variations to these model solutions are boundless.

2.5. The Canonicalization Based Approach

This approach is used extensively to identify alternate solutions to a given programming exercise is to convert the program code into a standardized form. The standardized form is then compared against a solution that is stored in the same standardized form. Different standardized forms have been proposed.

2.5.1. Linkage Graph Based Program Representation

A linkage graph is a directed acrylic graph whose nodes represent program statements and directed edges indicate dependencies between the different statements. This graph is represented as a two dimensional matrix. Equivalent programs have equal matrices, thereby allowing accepting alternative solutions to a single exercise [16]. However, the published work only deals with the assignment statement. The probability that this method will be able to produce equal matrices for logically equivalent programs using other programming structures is, as yet doubtful.

2.5.2. Abstract Syntax Tree (AST) Based Program Representation

The completed student solution is converted into an AST, which captures the structure of a program. The form of the AST is dependent on the structure of the program. Therefore, alternative solutions to a single program have different ASTs. This means that the AST obtained from the student’s program is converted to a standard form using a set of rules. Once a student’s solution has been converted into an AST, systems can gather relevant information on what data structures and algorithms the student is used by checking the tree [31], [34]. Although this method seems suitable for identifying alternative solutions to small programming exercises, it is difficult to see it being expandable for larger programs.

2.6. The Data-Driven Approach

2.6.1. Data-Driven Program Synthesis

I.   Data-Driven Programming Synthesis for Hint Generation in Programming Tutors

This method models programming directly in terms of textual edits, allowing us to trace student actions more closely. This one is generative: given an incorrect program, it finds a sequence of edits that transforms it into a correct solution. The goal of this method is to synthesis new programs from an incorrect solution [20]. One major drawback of this approach is the search algorithm. When searching for edit sequences, the scoring function only considers edits in the current sequence.

II. Accessible Programming Using Program Synthesis

The AutoProf [32] system for Python provides feedback for introductory programming exercises to students by telling them exactly what is wrong with their solution and how to correct it. Given the reference implementation and the error model, the synthesis algorithm symbolically searches over the space of all possible rewrites to a student solution and finds a corrected solution, which is functionally equivalent to the reference implementation and which requires minimum number of rewrites. This set of rewrites induces a large space of corrections (10¹⁵), and the AutoPro needs to check each one of them for functional equivalence. This system encodes this large solution space using constraints and uses an iterative minimization algorithm to efficiently solve them [32]. However, this is a first step towards using the power of automated program synthesis for democratizing programming, and there are many new exciting systems that can be built upon these foundations to make programming accessible to an even larger class of people.

2.6.2. Machine Learning (ML) of Solution Spaces

According to this method, solution spaces are automatically clustered by machine learning techniques operating on sets student solutions. Based on these structured solution spaces, system proposes feedback provision strategies that employ example based learning methods comparing student solution attempts to appropriate sample solutions [11]. The key problem with this method is that let us assume that a set of correct student solutions is given for a programming exercise. As described above, feedback can then be generated based on a sufficient number of examples, which are essentially high quality solutions, either included in a database of student solutions, or provided by teachers/experts as designated sample solutions.

2.6.3. The Intelligent Teaching Assistant for Programming (ITAP) System

The ITAP combines algorithms for state abstraction, path construction, and state reification to fully automate the process of hint generation, even when given states that have not occurred in the data before. ITAP makes it possible to generate a full chain of hints from any new code state to the closest goal state. Further, the ITAP is an instance of a self-improving ITS, a tutor that continually improves its ability to provide hints that are personalized to each students’ individual solution to a programming exercise.

The ITAP requires a two pieces of expert knowledge to run independently, though this knowledge is kept to a minimum. The needed data is: At least one reference solution to the problem (e.g. a teacher/expert exemplar) and a test method that can automatically score code (e.g. pairs of expected input and output). Both reference solutions and test methods are already commonly created by teachers/experts in the process of preparing assignments, so the burden of knowledge generation is not too large [31]. A major limitation of this method is that it relies on the existence of test cases that can measure the correctness of solutions. Though there are a large number of programming exercises which can easily be tested using input/output sets, there are many other programming exercises which are difficult to test; for example, graphical assignments, interactive programs, and programs using randomization.

2.6.4. Inferring Problem Solving Policies

Piech et al. have provided a definition of Problem Solving Policy (PSP): "PSP is a decision for any partial solution as to what next partial solution a student should take" (see the example in Figure 2). Furthermore, they claim "that data of how previous students navigated their way to the final answer can be leveraged to autonomously understand the landscape of such assessments and enable hints for future students," thereby potentially increasing future student retention [28].

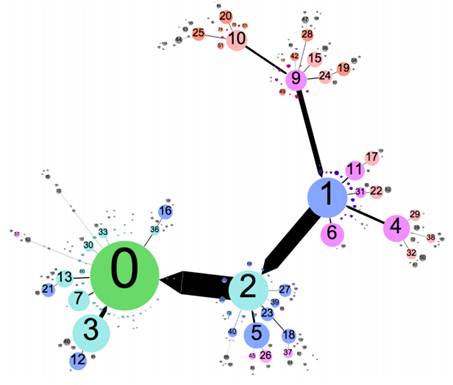
Figure 2. Each node is a unique partial solution, node 0 is the correct answer. The edges show what next partial solution they think a teacher/expert would suggest students move towards.

Piech et al. have offered a comparative analysis tested multiple solution space generation algorithms (including other’s path construction and their problem solving policies: all ten algorithms) from a MOOC (Massive Open Online Course: Code.org) to determine how often the selected next states matched the next states chosen by teachers/experts. They found that several of the algorithms had a high match rate, indicating that this new approach has great potential to generate the hints that students will benefit the most from.

2.6.5. The Variation Theory Based Method

Glassman et al. [8] proposed the use of variation theory to explain differences in student submissions. Applying variation theory to programming exercises essentially means using a hierarchical approach: first, distinguishing clusters of approaches to solving a problem, and then within each cluster identifying differences in various students’ implementation of a particular approach. This "divide and conquer" method has many other use cases, including pairing students based on their problem-solving strategies and making it easier to illustrate to students the relative merits of different approaches.

Gulwani et al. [13] studied a large number of functionally correct student solutions to introductory programming assignments and observed: (1) There are different algorithmic strategies, with varying levels of efficiency, for solving a given problem. These different strategies merit different feedback. (2) The same algorithmic strategy can be implemented in countless different ways.

However, the key problem with this method is that a teacher has to define an algorithmic strategy.

3. Conclusions

The objective of this research is to identify and category the current approaches to handling large solution space of ITSs for programming.

The primary contributions of this paper are:

• A review of existing ITSs for programming with many different programming languages and different programming paradigms from year 1976 to year 2015 and

• A brief review of recent approaches for solution space problem in the context of ITSs for programming.

In the context of student solution, existing ITSs for programming may be divided into two categories which are 1) incomplete/partial solutions and 2) complete/final/full solutions. Data-Drive approach is suitable for ITSs for programming with incomplete/partial solutions. Data-driven methods have been a successful approach to covering solution spaces for programming exercises of ITSs for programming. An advantage of this data-driven approach is that the instructor does not have to provide any input. On the other hand, it requires the existence of a large data set. Furthermore, in this approach, most of these algorithms have only been evaluated on collected student programming exercise solving traces, and the ones that are being tested on real students are implemented in online learning environments such as MOOCs not in individual classrooms. In a typical course, each topic is presented in a specific lecture on a specific date according to the course curriculum, and, at each moment of time, students are expected to focus on the current topic(s). To reflect this classroom practice, Data-Driven ITSs for programming should maintain the course schedule, which associates each topic with the date of its presentation.

Only one system, the ITAP is an instance of a self-improving ITS, a tutor that continually improves its ability to provide hints that are personalized to each students’ individual solution to a programming exercise. It does so by updating the solution space every time a student attempts a solution and recalculating optimal paths.

In summary, for the informants in this study, compared to others, the data-driven approach is flexible.

References

1. Ade-Ibijola, A., Ewert, S., & Sanders, I. (2015). Introducing Code Adviser: A DFA-driven Electronic Programming Tutor. In Implementation and Application of Automata (pp. 307-312). Springer International Publishing.
2. AlShamsi, F., & Elnagar, A. (2009, December). JLearn-DG: Java learning system using dependence graphs. In Proceedings of the 11th International Conference on Information Integration and Web-based Applications & Services (pp. 633-637). ACM.
3. Assaf, D., Escherle, N., Basawapatna, A., Maiello, C., & Repenning, A. Retention of Flow: Evaluating a Computer Science Education Week Activity.
4. Brusilovsky, P., & Peylo, C. (2003). Adaptive and intelligent web-based educational systems. International Journal of Artificial Intelligence in Education (IJAIED), 13, 159-172.
5. Chrysafiadi, K., & Virvou, M. (2014, July). KEM Cs: A set of student's characteristics for modeling in adaptive programming tutoring systems. InInformation, Intelligence, Systems and Applications, IISA 2014, The 5th International Conference on (pp. 106-110). IEEE.
6. Fossati, D., Di Eugenio, B., Ohlsson, S. T. E. L. L. A. N., Brown, C., & Chen, L. (2015). Data driven automatic feedback generation in the iList intelligent tutoring system. Technology, Instruction, Cognition and Learning, 10(1), 5-26.
7. Glassman, E. L., Scott, J., Singh, R., Guo, P. J., & Miller, R. C. (2015). OverCode: Visualizing variation in student solutions to programming problems at scale. ACM Transactions on Computer-Human Interaction (TOCHI), 22(2), 7.
8. Glassman, E. L., Singh, R., & Miller, R. C. (2014, March). Feature engineering for clustering student solutions. In Proceedings of the first ACM conference on Learning@ scale conference (pp. 171-172). ACM.
9. Gómez-Albarrán, M. (2005). The Teaching and Learning of Programming: A Survey of Supporting Software Tools. The Computer Journal, 48(2), 130-144.
10. Gerdes, A. (2012). Ask-Elle: a Haskell Tutor. PhD thesis, Universiteit Utrecht.
11. Gross, S., Mokbel, B., Paassen, B., Hammer, B., & Pinkwart, N. (2014). Example-based feedback provision using structured solution spaces. International Journal of Learning Technology 10, 9(3), 248-280.
12. Gross, S., & Pinkwart, N. (2015, July). Towards an Integrative Learning Environment for Java Programming. In Advanced Learning Technologies (ICALT), 2015 IEEE 15th International Conference on (pp. 24-28). IEEE.
13. Gulwani, S., Radiček, I., & Zuleger, F. (2014, November). Feedback generation for performance problems in introductory programming assignments. In Proceedings of the 22nd ACM SIGSOFT International Symposium on Foundations of Software Engineering (pp. 41-51). ACM.
14. Holland, J. (2009). A Constraint-Based ITS for the Java Programming Language (Doctoral dissertation, University of Canterbury). Retrieved from https://www.csse.canterbury.ac.nz/research/reports.
15. Igwe, K., Pillay, N., Corchado, E., Yun-Huoy, C., & Ma, K. (2013, December). Automatic Programming Using Genetic Programming. In Proceedings of the World Congress on Information and Communication Technologies., Hanoi, Vietnam (pp. 339-344).
16. Jin, W., Barnes, T., Stamper, J., Eagle, M. J., Johnson, M. W., & Lehmann, L. (2012, January). Program representation for automatic hint generation for a data-driven novice programming tutor. In Intelligent Tutoring Systems (pp. 304-309). Springer Berlin Heidelberg.
17. Keuning, H. (2014). Strategy-based feedback for imperative programming exercises. PhD thesis, Utrecht University.
18. Keuning, H., Heeren, B., & Jeuring, J. (2014, November). Strategy-based feedback in a programming tutor. In Proceedings of the Computer Science Education Research Conference (pp. 43-54). ACM.
19. Lahtinen, E., Ala-Mutka, K., & Järvinen, H. M. (2005, June). A study of the difficulties of novice programmers. In ACM SIGCSE Bulletin (Vol. 37, No. 3, pp. 14-18). ACM.
20. Lazar, T., & Bratko, I. (2014, January). Data-Driven Program Synthesis for Hint Generation in Programming Tutors. In Intelligent Tutoring Systems (pp. 306-311). Springer International Publishing.
21. Le, N.-T. (2011). Using weighted constraints to build a tutoring system for logic programming. (PhD thesis), University of Hamburg, Germany.
22. Le, N. T., Loll, F., & Pinkwart, N. (2013). Operationalizing the Continuum between Well-Defined and Ill-Defined Problems for Educational Technology. Learning Technologies, IEEE Transactions on, 6(3), 258-270.
23. Lee, M. R., & Chen, T. T. (2015). Digital creativity: Research themes and framework. Computers in Human Behavior, 42, 12-19.
24. Luxton-Reilly, A., Denny, P., Kirk, D., Tempero, E., & Yu, S. Y. (2013, July). On the differences between correct student solutions. In Proceedings of the 18th ACM conference on Innovation and technology in computer science education(pp. 177-182). ACM.
25. Maghdid, D., Szybek, P., & Führer, C. (2015). A Study on Variation Technique in Courses on Scientific Computing. Science Journal of Education, 3(June 2015), 60-67.
26. Nguyen, A., Piech, C., Huang, J., & Guibas, L. (2014, April). Codewebs: scalable homework search for massive open online programming courses. InProceedings of the 23rd international conference on World wide web (pp. 491-502). ACM.
27. Paaßen, B., Mokbel, B., & Hammer, B. (2015). Adaptive structure metrics for automated feedback provision in Java programming. In English. In: European Symposium on Artificial Neural Networks (ESANN). Ed. by Michel Verleysen.(accepted/in press). Bruges, Belgium.
28. Piech, C., Sahami, M., Huang, J., & Guibas, L. (2015, March). Autonomously Generating Hints by Inferring Problem Solving Policies. In Proceedings of the Second (2015) ACM Conference on Learning@ Scale (pp. 195-204). ACM.
29. Rivers, K., & Koedinger, K. R. (2012, January). A canonicalizing model for building programming tutors. In Intelligent Tutoring Systems (pp. 591-593). Springer Berlin Heidelberg.
30. Price, T. W., & Barnes, T. (2015, June). An exploration of data-driven hint generation in an open-ended programming problem. In Workshop on Graph-Based Data Mining held at Educational Data Mining (EDM).
31. Rivers, K., & Koedinger, K. R. (2015). Data-Driven Hint Generation in Vast Solution Spaces: a Self-Improving Python Programming Tutor. International Journal of Artificial Intelligence in Education, 1-28.
32. Singh, R. (2014). Accessible programming using program synthesis (Doctoral dissertation, Massachusetts Institue of Technology).
33. Sudol, L. A., Rivers, K., & Harris, T. K. (2012). Calculating Probabilistic Distance to Solution in a Complex Problem Solving Domain. International Educational Data Mining Society.
34. Truong, N. (2007). A web-based programming environment for novice programmers (Doctoral dissertation, Queensland University of Technology).
35. Thuné, M., & Eckerdal, A. (2009). Variation theory applied to students’ conceptions of computer programming. European Journal of Engineering Education, 34(4), 339-347.
36. Weragama, D. S. (2013). Intelligent tutoring system for learning PHP. PhD thesis, Queensland University of Technology.